2025数维杯 B题国一团队

更新 【完整每问手把手详细思路+建模过程+算法代码】70页+

【高质量成品论文】+

更新 3GB配套升级求解Matlab/Python双版本【代码】+

更新2GB每问完整详细数据+

更新可视化图表源文件+

+国一学长 思路代码讲解视频

质量均为一等奖水平，先到先得!

可参考往期作品https://mbd.pub/o/bread/mbd-ZpWUlJtv https://mbd.pub/o/bread/mbd-ZJyTlJhw，https://mbd.pub/o/bread/mbd-ZJqalZxx，https://mbd.pub/o/bread/mbd-ZJqUlZ9p

更新 【完整每问手把手详细思路+建模过程+算法代码】70页

已更新 3GB 配套升级求解【代码】+2GB数据

已更新 各类可视化图表

完整代码共计2000多行！

《西安马拉松赛事规划与纪念品设计》

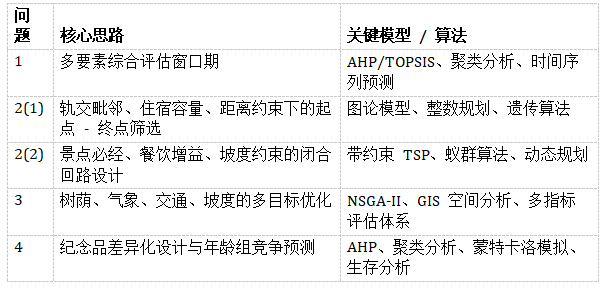
问题 1：筛选马拉松赛事窗口期

思路分析

核心要素量化：

气象适宜性：基于附件 1 气象数据（气温、降水、风速等），定义适宜办赛的气象阈值（如气温 10-25℃，无暴雨，风速≤6 级），计算各城市逐月气象适宜天数。

城市承载能力：结合附件 3 人口普查数据（人口规模、年龄结构）、附件 4 人口密度，评估城市基础设施（住宿、交通）承载赛事的最大容量，避免过度消耗资源。

报名热度：通过附件 12 赛历数据统计历史报名人数及增长率，识别热门城市 / 时段，结合时间序列预测未来报名趋势。

综合筛选：对城市逐月数据加权评分，筛选出气象适宜、承载能力充足且报名热度高的时段作为窗口期。

数学模型与算法

多指标综合评价模型（如层次分析法 AHP、TOPSIS）：确定气象、承载能力、报名热度的权重，计算综合得分。

聚类分析：按城市规模、气候带对城市分类，分别筛选窗口期。

时间序列模型（如 ARIMA）：预测报名人数增长率，辅助判断时段热度。

问题 2：西安马拉松路线设计

子问题 2 (1)：起点 - 终点组合筛选

约束条件处理：

距离≥42km：基于附件 7 西安道路数据，构建道路网络图，搜索满足距离约束的起点 - 终点对。

住宿容量≥3000 人（起点 3km 内）：利用附件 5 住宿设施坐标，通过缓冲区分析（3km 半径）统计住宿容量。

毗邻轨交站点：结合附件 8/9 公交 / 地铁数据，要求起终点 500m 内有轨交站点。

目标优化：最小化路线绕行度（或最大化景观覆盖），同时满足约束。

数学模型与算法

图论模型：将道路网络抽象为图，节点为轨交站点，边为路段（含距离、住宿容量属性）。

整数规划模型：以起点 - 终点距离≥42km、住宿容量≥3000 人为约束，目标函数为路线合理性（如连通性、轨交便利性）。

启发式算法（如遗传算法、模拟退火）：在大规模路网中搜索可行解。

子问题 2 (2)：含景点 / 餐饮节点的闭合回路设计

节点定义：

必经节点：附件 5 中的景点，需串联形成路线核心。

增益节点：餐饮设施，每经过 1 个增益 0.2，需每 5km 设置补给站（邻近餐饮）。

坡度约束：利用附件 6 地形数据，确保路段坡度≤5%。

路线设计：闭合回路需满足全马（42.195km）、半马（21.0975km）、健康跑（5/10km）距离，同时最大化增益值。

数学模型与算法

带约束的旅行商问题（TSP）：将景点作为必经节点，餐饮作为可选增益节点，构建含距离、坡度、补给站间隔约束的路径优化模型。

动态规划：按距离分段（每 5km）设置补给站，确保邻近餐饮设施。

蚁群算法：处理多距离（全马 / 半马 / 健康跑）的路径搜索，平衡增益值与约束条件。

问题 3：多目标优化与路线评估

思路分析

量化分析：

树荫覆盖率：基于附件 10 绿地数据，计算赛道沿线树木覆盖长度占比，结合附件 7 道路数据定位高暴露路段。

气象数据优化：利用附件 1 气温、太阳辐射数据，识别高温时段（如 9:00-16:00），避免路线在该时段暴露于直射阳光。

交通影响：通过附件 8/9 轨交数据评估赛道对交通的阻断程度，计算绕行距离或拥堵指数。

多目标平衡：最小化高温暴露距离、交通干扰，同时考虑坡度（来自附件 6）对选手体验的影响。

数学模型与算法

多目标优化算法（如 NSGA-II、MOEA/D）：以 “树荫覆盖最大化”“高温暴露距离最小化”“交通影响最小化”“坡度平缓化” 为目标，生成 Pareto 前沿解。

空间分析工具（GIS 缓冲区、叠加分析）：量化树荫覆盖与气象数据的时空关联。

评估指标：

高温暴露指数（暴露距离 / 总赛程）

交通拥堵系数（受影响路段客流量占比）

平均坡度与坡度波动值

问题 4：纪念品设计与年龄分组优化

思路分析

限定纪念品设计：

结合赛事主题（如西安历史文化），设计具有地域特色的纪念品（如定制奖牌、城市地标盲盒），通过用户调研（或附件 11 马拉松大数据）分析收藏价值影响因素（稀缺性、文化内涵、实用性）。

差异化权益：按参赛组别（全马 / 半马 / 健康跑）、成绩排名（如前 10%、前 50%）设置兑换权限（如专属纪念品、免费住宿券）。

年龄分组优化：

按 5 岁间隔细分年龄组（如 20-24 岁，25-29 岁），利用附件 3 人口普查数据计算各组人数，结合历史成绩数据（附件 11）统计各组完赛时间分布，预测竞争激烈程度（如标准差、完赛率）。

赛前模拟排名工具：基于蒙特卡洛模拟，输入选手历史成绩，预测其在目标年龄组的排名概率。

数学模型与算法

层次分析法（AHP）：确定纪念品设计要素权重（文化性、收藏性、实用性），评估设计方案。

聚类分析（如 K-means）：根据历史成绩将年龄组划分为不同竞争等级（激烈 / 中等 / 温和）。

生存分析（Kaplan-Meier 模型）：预测各组选手完赛时间分布，辅助制定奖励方案。

蒙特卡洛模拟：生成大量虚拟比赛成绩，模拟选手在细分年龄组中的排名分布。

总结

完整内容介绍见链接：https://mbd.pub/o/bread/mbd-aZ6cmZhx

获奖率达99%：以下是去年深圳杯/东三省数学建模一等奖助攻记录