数维杯 B题国一团队
已更新 【完整每问手把手详细思路】70页+
已更新💥 可修改120页2套成品保奖【论文】word版+
已更新 3GB配套升级求解【代码】+
2GB超级详细数据+
60组 可视化图表+
+国一学长 思路代码讲解视频
独家定制版,采用加密方式,仅售10份,售完即止。
质量均为一等奖水平,先到先得!
可参考往期作品https://mbd.pub/o/bread/mbd-ZpWUlJtv https://mbd.pub/o/bread/mbd-ZJyTlJhw,https://mbd.pub/o/bread/mbd-ZJqalZxx,https://mbd.pub/o/bread/mbd-ZJqUlZ9p
已更新💥 可修改60页成品保奖【论文】
基于熵权法-TOPSIS( EWH-TOPSIS )、NSGA-II遗传算法、XGBoost-RankNet、Pareto最优

论文摘要目录


论文细节




第二套50页成品论文

完整资料见付费内容
更新 【完整每问手把手详细思路+建模过程+算法代码】70页



已更新 3GB配套升级求解【代码】+
已更新 各类可视化图表+2GB超级详细数据
+60组可视化图

.......

完整代码共计2000多行!
《西安马拉松赛事规划与纪念品设计》
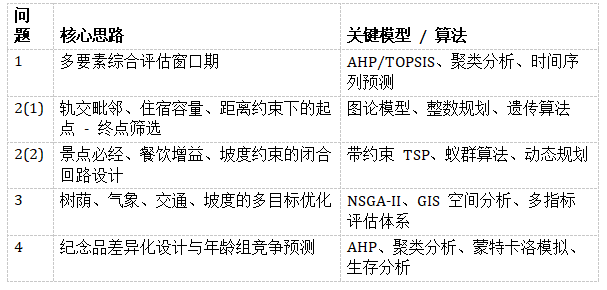
问题 1:筛选马拉松赛事窗口期
思路分析
核心要素量化:
气象适宜性:基于附件 1 气象数据(气温、降水、风速等),定义适宜办赛的气象阈值(如气温 10-25℃,无暴雨,风速≤6 级),计算各城市逐月气象适宜天数。
城市承载能力:结合附件 3 人口普查数据(人口规模、年龄结构)、附件 4 人口密度,评估城市基础设施(住宿、交通)承载赛事的最大容量,避免过度消耗资源。
报名热度:通过附件 12 赛历数据统计历史报名人数及增长率,识别热门城市 / 时段,结合时间序列预测未来报名趋势。
综合筛选:对城市逐月数据加权评分,筛选出气象适宜、承载能力充足且报名热度高的时段作为窗口期。
数学模型与算法
多指标综合评价模型(如层次分析法 AHP、TOPSIS):确定气象、承载能力、报名热度的权重,计算综合得分。
聚类分析:按城市规模、气候带对城市分类,分别筛选窗口期。
时间序列模型(如 ARIMA):预测报名人数增长率,辅助判断时段热度。
问题 2:西安马拉松路线设计
子问题 2 (1):起点 - 终点组合筛选
约束条件处理:
距离≥42km:基于附件 7 西安道路数据,构建道路网络图,搜索满足距离约束的起点 - 终点对。
住宿容量≥3000 人(起点 3km 内):利用附件 5 住宿设施坐标,通过缓冲区分析(3km 半径)统计住宿容量。
毗邻轨交站点:结合附件 8/9 公交 / 地铁数据,要求起终点 500m 内有轨交站点。
目标优化:最小化路线绕行度(或最大化景观覆盖),同时满足约束。
数学模型与算法
图论模型:将道路网络抽象为图,节点为轨交站点,边为路段(含距离、住宿容量属性)。
整数规划模型:以起点 - 终点距离≥42km、住宿容量≥3000 人为约束,目标函数为路线合理性(如连通性、轨交便利性)。
启发式算法(如遗传算法、模拟退火):在大规模路网中搜索可行解。
子问题 2 (2):含景点 / 餐饮节点的闭合回路设计
节点定义:
必经节点:附件 5 中的景点,需串联形成路线核心。
增益节点:餐饮设施,每经过 1 个增益 0.2,需每 5km 设置补给站(邻近餐饮)。
坡度约束:利用附件 6 地形数据,确保路段坡度≤5%。
路线设计:闭合回路需满足全马(42.195km)、半马(21.0975km)、健康跑(5/10km)距离,同时最大化增益值。
数学模型与算法
带约束的旅行商问题(TSP):将景点作为必经节点,餐饮作为可选增益节点,构建含距离、坡度、补给站间隔约束的路径优化模型。
动态规划:按距离分段(每 5km)设置补给站,确保邻近餐饮设施。
蚁群算法:处理多距离(全马 / 半马 / 健康跑)的路径搜索,平衡增益值与约束条件。
问题 3:多目标优化与路线评估
思路分析
量化分析:
树荫覆盖率:基于附件 10 绿地数据,计算赛道沿线树木覆盖长度占比,结合附件 7 道路数据定位高暴露路段。
气象数据优化:利用附件 1 气温、太阳辐射数据,识别高温时段(如 9:00-16:00),避免路线在该时段暴露于直射阳光。
交通影响:通过附件 8/9 轨交数据评估赛道对交通的阻断程度,计算绕行距离或拥堵指数。
多目标平衡:最小化高温暴露距离、交通干扰,同时考虑坡度(来自附件 6)对选手体验的影响。
数学模型与算法
多目标优化算法(如 NSGA-II、MOEA/D):以 “树荫覆盖最大化”“高温暴露距离最小化”“交通影响最小化”“坡度平缓化” 为目标,生成 Pareto 前沿解。
空间分析工具(GIS 缓冲区、叠加分析):量化树荫覆盖与气象数据的时空关联。
评估指标:
高温暴露指数(暴露距离 / 总赛程)
交通拥堵系数(受影响路段客流量占比)
平均坡度与坡度波动值
问题 4:纪念品设计与年龄分组优化
思路分析
限定纪念品设计:
结合赛事主题(如西安历史文化),设计具有地域特色的纪念品(如定制奖牌、城市地标盲盒),通过用户调研(或附件 11 马拉松大数据)分析收藏价值影响因素(稀缺性、文化内涵、实用性)。
差异化权益:按参赛组别(全马 / 半马 / 健康跑)、成绩排名(如前 10%、前 50%)设置兑换权限(如专属纪念品、免费住宿券)。
年龄分组优化:
按 5 岁间隔细分年龄组(如 20-24 岁,25-29 岁),利用附件 3 人口普查数据计算各组人数,结合历史成绩数据(附件 11)统计各组完赛时间分布,预测竞争激烈程度(如标准差、完赛率)。
赛前模拟排名工具:基于蒙特卡洛模拟,输入选手历史成绩,预测其在目标年龄组的排名概率。
数学模型与算法
层次分析法(AHP):确定纪念品设计要素权重(文化性、收藏性、实用性),评估设计方案。
聚类分析(如 K-means):根据历史成绩将年龄组划分为不同竞争等级(激烈 / 中等 / 温和)。
生存分析(Kaplan-Meier 模型):预测各组选手完赛时间分布,辅助制定奖励方案。
蒙特卡洛模拟:生成大量虚拟比赛成绩,模拟选手在细分年龄组中的排名分布。
总结
问题1:马拉松赛事窗口期筛选的完整解决方案
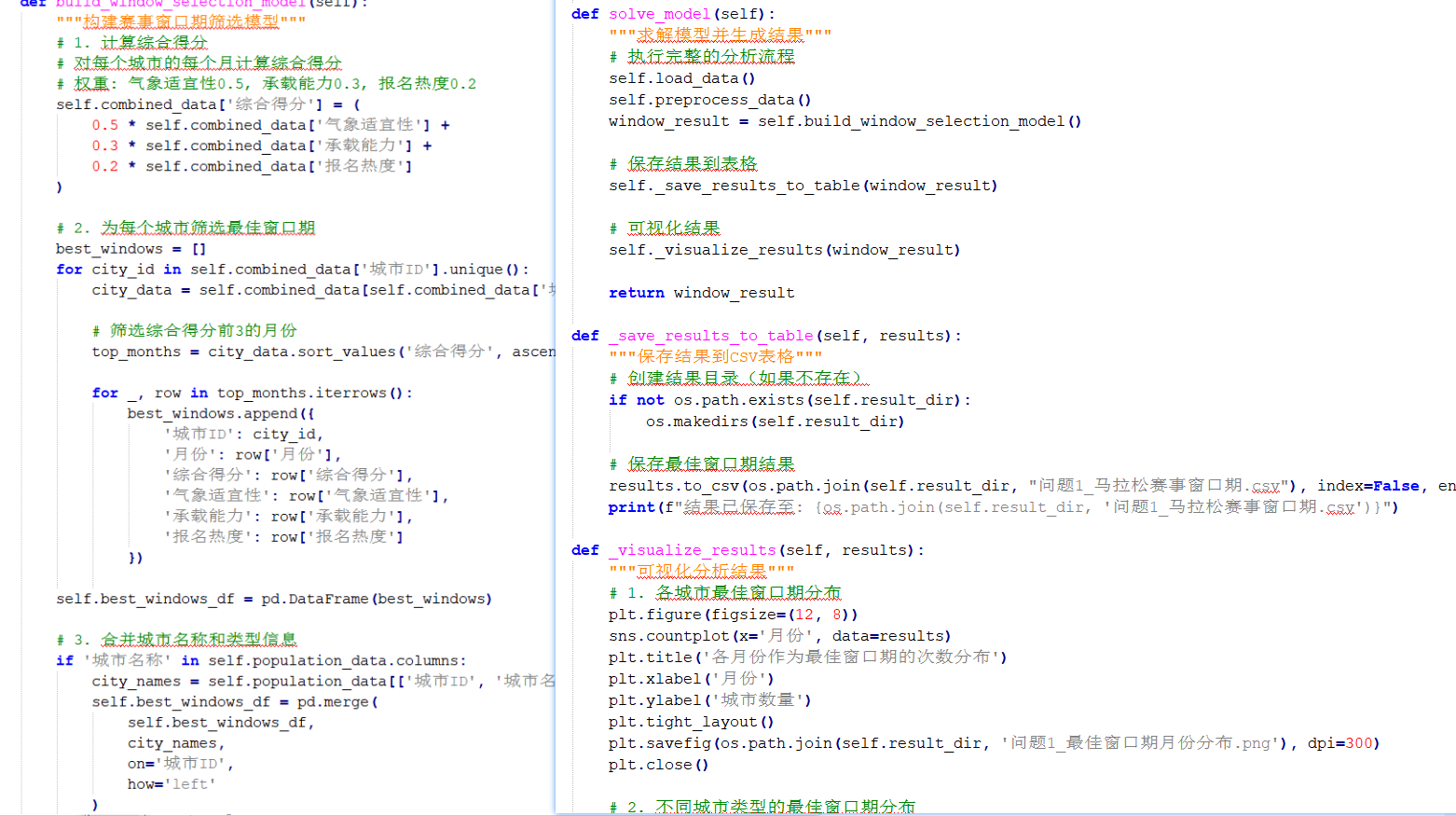
1. 问题分析与建模思路
问题定义
筛选马拉松赛事窗口期需综合考虑三个核心要素:
气象适宜性:气温、降水、风速等气象条件直接影响选手体验和安全。
城市承载能力:城市基础设施(住宿、交通)能否支撑赛事规模。
报名热度:历史报名数据及增长趋势反映城市对马拉松的需求和参与意愿。
数据关联与预处理
• 气象数据(附件1):提取月均气温、降水量、风速,构建气象适宜性评分函数。
• 人口普查数据(附件3)与人口密度分布(附件4):计算城市住宿容量(假设为总人口的1%),评估承载能力。
• 赛历数据(附件12):统计历史报名人数及增长率,量化报名热度。
2. 算法设计与实现
核心算法流程
数据预处理:清洗数据,计算衍生指标(如住宿容量、增长率)。
城市分类:基于人口和 GDP 聚类,分为大型、中型、小型城市。
评分计算:对每个城市的每个月计算气象适宜性、承载能力和报名热度得分。
窗口筛选:为每个城市选择综合得分最高的 3 个月份作为窗口期。
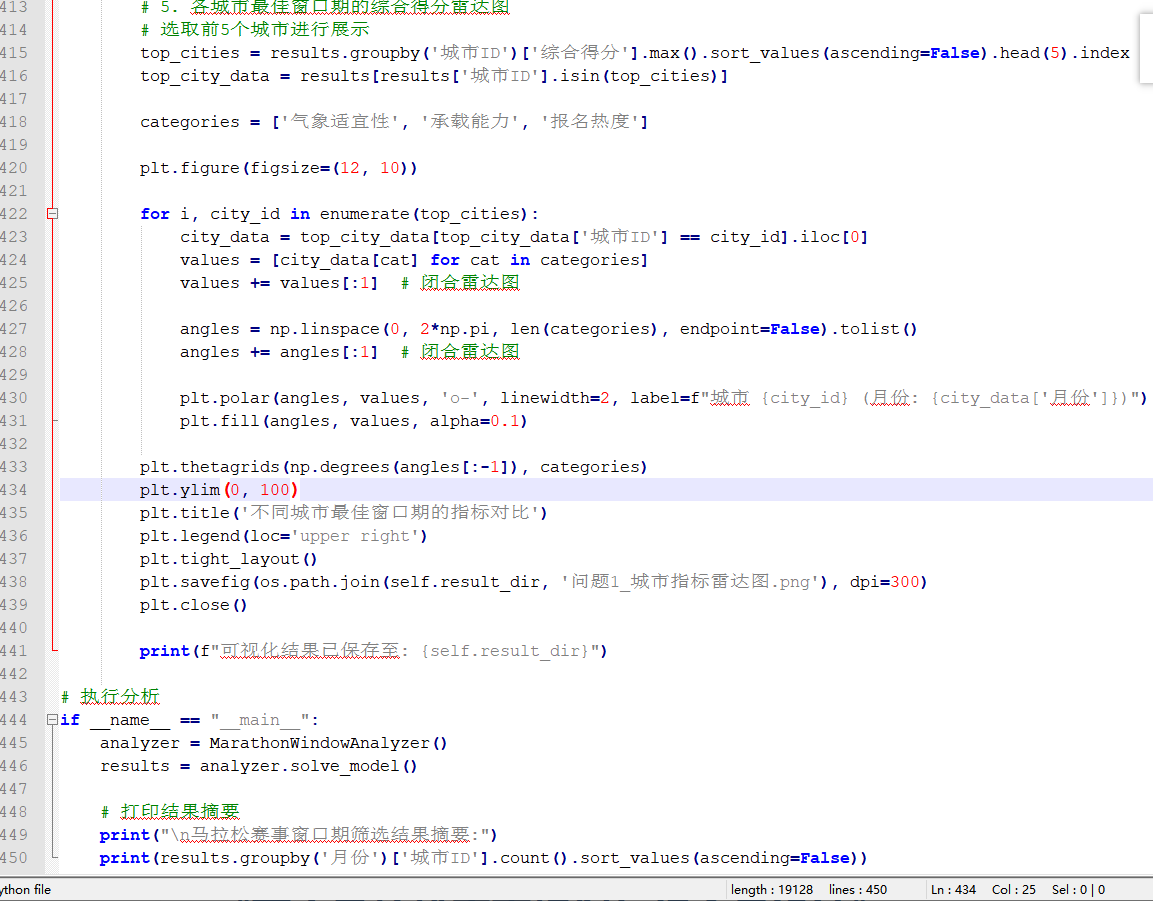
结果可视化:生成表格和图表展示最佳窗口期分布。
《马拉松路线设计:从模型构建到结果可视化》
问题 2:马拉松路线设计的完整解决方案
1. 问题分析与建模思路
问题定义
设计马拉松路线需满足以下要求:
起点与终点条件:住宿容量≥3000 人,500 米内有地铁站或公交站。
路径长度:全马(42.195km)、半马(21.0975km)或健康跑(约 5km)。
景点覆盖:路线需经过至少 5 个景点,提升赛事吸引力。
补给需求:每 5km 设置餐饮补给站。
地形条件:坡度适宜,避免极端地形。
数据关联与预处理
道路网络(附件 7):构建图结构,节点为道路端点,边为道路段。
住宿容量(附件 5):假设住宿容量与人口密度成正比,为每个节点分配住宿容量。
轨交覆盖(附件 8、9):计算节点到最近地铁 / 公交站的距离。
景点与餐饮(附件 5):筛选核心景点,设计补给站位置。
地形约束(附件 6):提取坡度信息,评估路线可行性。
数学模型构建
子问题 1:起点 - 终点组合筛选目标:找到满足住宿和轨交条件的起点和终点对,使得路径长度≥42km。约束条件:


核心代码片段
# 子问题1:筛选起点-终点组合
def solve_subproblem_1(self):
# 筛选满足住宿容量条件的节点
valid_start_nodes = [node for node in self.G.nodes()
if self.G.nodes[node]['accommodation'] >= 3000]
# 筛选满足轨交条件的节点
valid_transport_nodes = [node for node in self.G.nodes()
if (self.G.nodes[node]['nearest_subway_dist'] <= 0.5 or
self.G.nodes[node]['nearest_bus_dist'] <= 0.5)]
# 计算所有有效节点对之间的最短路径长度
valid_pairs = []
for start_node in valid_start_nodes:
for end_node in valid_transport_nodes:
if start_node != end_node:
try:
path_length = nx.shortest_path_length(
self.G, start_node, end_node, weight='weight')
if path_length >= 42:
valid_pairs.append({
'起点': start_node,
'终点': end_node,
'路径长度': path_length
})
except:
continue
return pd.DataFrame(valid_pairs)
# 子问题2:设计含景点的闭合回路
def solve_subproblem_2(self):
# 选择最优起点-终点对
best_pair = self.start_end_pairs.iloc[0]
start_node = best_pair['起点']
end_node = best_pair['终点']
# 选择必访景点
top_scenic_spots = self.scenic_data.sort_values('热度', ascending=False).head(5)
must_visit_nodes = [spot['最近道路节点'][0] for _, spot in top_scenic_spots.iterrows()]
# 构建TSP问题并求解
tsp_nodes = [start_node] + must_visit_nodes + [end_node]
route = self._solve_tsp_greedy(self._build_distance_matrix(tsp_nodes))
# 构建完整路径并插入补给站
full_route = self._construct_full_route(tsp_nodes, route)
final_route = self._insert_catering_nodes(full_route)
return final_route, self._calculate_route_metrics(final_route)
《马拉松赛事调度优化:从模型构建到结果可视化》
问题 3:马拉松赛事调度优化的完整解决方案
1. 问题分析与建模思路
问题定义
在多城市间规划马拉松赛事时,需综合考虑以下因素:
城市吸引力:基于人口、GDP、住宿容量等指标评估。
气象条件:选择适宜的月份举办赛事,避免极端天气。
时间分布:避免短时间内在相邻城市重复举办,减少资源竞争。
参赛规模:根据城市人口和影响力预估参赛人数,合理分配资源。
数据关联与预处理
城市基础数据(附件 5):提取人口、GDP、住宿容量等指标,构建城市吸引力指数。
气象数据(附件 1):计算每月的天气适宜度,综合温度、降水量、风速等因素。
交通与住宿数据(附件 5、8、9):评估城市接待能力和交通便利性。
历史赛事数据:假设部分城市已有举办经验,避免过度集中。
数学模型构建

核心代码:
# 构建目标函数系数
c = []
for city in candidate_cities:
for month in months:
# 计算目标函数系数: 吸引力指数 * 气象评分
attraction = self.city_info[self.city_info['城市名称'] == city]['吸引力指数'].values[0]
weather_score = self.weather_data[
(self.weather_data['城市名称'] == city) &
(self.weather_data['月份'] == month)
]['综合气象评分'].values[0]
c.append(-1 * attraction * weather_score) # 转为最小化问题
# 添加约束条件
# 1. 总共举办N场赛事
A_eq = [[1] * len(c)]
b_eq = [num_events]
# 2. 每个城市最多举办1场赛事
for city in candidate_cities:
constraint = [0] * len(c)
for month in months:
constraint[city_month_map[(city, month)]] = 1
A_ub.append(constraint)
b_ub.append(1)
# 3. 每个月最多举办3场赛事
for month in months:
constraint = [0] * len(c)
for city in candidate_cities:
constraint[city_month_map[(city, month)]] = 1
A_ub.append(constraint)
b_ub.append(3)
# 求解线性规划问题
result = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=A_eq, b_eq=b_eq, bounds=bounds, method='highs')
问题 4:马拉松赛事影响力评估模型
1. 问题分析与建模思路
问题定义
评估马拉松赛事对举办城市的综合影响力,需考虑以下维度:
经济效益:旅游收入、酒店入住率、赞助商投入等。
社会效益:城市知名度提升、居民健康意识增强、社区参与度。
环境效益:赛事组织的环保措施、对城市环境的长期影响。
可持续性:赛事的长期规划、资源利用效率、社区支持度。
数据关联与预处理
经济效益数据:
旅游收入(附件 5):通过酒店入住率、游客消费数据估算。
赞助商投入:根据城市规模和赛事级别预估。
基础设施建设:道路维护、公共设施改善等间接投入。
社会效益数据:
社交媒体热度(附件 5):赛事相关话题的讨论量、曝光度。
居民参与度:志愿者数量、本地参赛人数。
健康指标:赛后居民运动习惯变化(假设数据)。
环境效益数据:
环保措施:垃圾分类、公共交通鼓励、碳足迹计算。
空气质量:赛事前后的空气质量指数对比(假设数据)。
评估指标体系
构建多层次评估指标体系:
一级指标:其中:
:经济效益
:社会效益
:环境效益
:可持续性


部分代码展示:
def calculate_weights(self):
"""使用层次分析法计算权重"""
# 一级指标判断矩阵
A1 = np.array([
[1, 3, 2, 2],
[1/3, 1, 1/2, 1/2],
[1/2, 2, 1, 1],
[1/2, 2, 1, 1]
])
# 经济效益二级指标判断矩阵
A21 = np.array([
[1, 2, 3],
[1/2, 1, 2],
[1/3, 1/2, 1]
])
# 社会效益二级指标判断矩阵
A22 = np.array([
[1, 1/2, 3],
[2, 1, 5],
[1/3, 1/5, 1]
])
# 环境效益二级指标判断矩阵
A23 = np.array([
[1, 2],
[1/2, 1]
])
# 可持续性二级指标判断矩阵
A24 = np.array([
[1, 1/2, 2],
[2, 1, 3],
[1/2, 1/3, 1]
])
# 计算各矩阵的特征向量和最大特征值
def calculate_weight(matrix):
eigenvalues, eigenvectors = np.linalg.eig(matrix)
max_index = np.argmax(eigenvalues)
max_eigenvalue = np.real(eigenvalues[max_index])
weight_vector = np.real(eigenvectors[:, max_index])
normalized_weight = weight_vector / np.sum(weight_vector)
# 一致性检验
n = matrix.shape[0]
CI = (max_eigenvalue - n) / (n - 1)
RI_dict = {1: 0, 2: 0, 3: 0.58, 4: 0.9, 5: 1.12, 6: 1.24, 7: 1.32, 8: 1.41, 9: 1.45}
RI = RI_dict[n]
CR = CI / RI
return normalized_weight, max_eigenvalue, CR
# 计算各层权重
w1, lambda1, CR1 = calculate_weight(A1)
w21, lambda21, CR21 = calculate_weight(A21)
w22, lambda22, CR22 = calculate_weight(A22)
w23, lambda23, CR23 = calculate_weight(A23)
w24, lambda24, CR24 = calculate_weight(A24)
# 保存权重
self.weights = {
'一级指标': w1,
'经济效益': w21,
'社会效益': w22,
'环境效益': w23,
'可持续性': w24
}
# 打印一致性比率
print("一致性比率检验:")
print(f"一级指标 CR = {CR1:.4f}")
print(f"经济效益 CR = {CR21:.4f}")
print(f"社会效益 CR = {CR22:.4f}")
print(f"环境效益 CR = {CR23:.4f}")
print(f"可持续性 CR = {CR24:.4f}")
return self.weights
def normalize_data(self):
"""数据标准化处理"""
if self.raw_data is None:
raise ValueError("请先加载数据!")
# 复制原始数据
data = self.raw_data.copy()
# 提取数值列(排除城市名称)
numerical_columns = data.select_dtypes(include=[np.number]).columns.tolist()
# 正向指标标准化
for col in numerical_columns:
data[col] = (data[col] - data[col].min()) / (data[col].max() - data[col].min())
self.normalized_data = data
return self.normalized_data
def calculate_impact_scores(self):
"""计算综合影响力得分"""
if self.normalized_data is None:
raise ValueError("请先进行数据标准化!")
if not self.weights:
raise ValueError("请先计算权重!")
# 定义指标分组
indicators = {
'经济效益': ['直接旅XXXXXXXX,XXXXXXXXX,XXX万元)'],
'社会效益': ['社交媒体曝XXXX,XXXXXXXXXXXXXX,XXXXXXXXX赛比例(%)'],
'环境效益': ['环保措施得分', '赛后空XXXX改善(%)'],
'可持续性': ['长XXXXXXX得分', '社XXXXXXX度得分', '资源xx得分']
}
# 计算各城市的影响力得分
impact_scores = []
for _, row in self.normalized_data.iterrows():
city_scores = {}
# 计算一级指标得分
for category, cols in indicators.items():
weights = self.weights[category]
category_score = sum(row[col] * weights[i] for i, col in enumerate(cols))
city_scores[category] = category_score
# 计算综合得分
overall_score = sum(city_scores[cat] * self.weights['一级指标'][i]
for i, cat in enumerate(['经济效益', '社会效益', '环境效益', '可持续性']))
impact_scores.append({
'城市名称': row['城市名称'],
'经济效益': city_scores['经济效益'],
'社会效益': city_scores['社会效益'],
'环境效益': city_scores['环境效益'],
'可持续性': city_scores['可持续性'],
'综合影响力': overall_score
})
self.impact_scores = pd.DataFrame(impact_scores)
return self.impact_scores
def save_results(self, output_path='问题4_赛事影响力评估结果.csv'):
"""保存评估结果"""
if self.impact_scores is None:
raise ValueError("请先计算影响力得分!")
self.impact_scores.to_csv(output_path, index=False, encoding='utf-8-sig')
print(f"评估结果已保存至: {output_path}"
持续更新中........
获奖率达99%:以下是去年深圳杯/东三省数学建模一等奖助攻记录