赛题的【每问超级详细手把手思路教学➕详细数学模型建立求解文档 + 完美运行求解代码➕参考文献】（都会在第一时间更新上传的，所有的资料数据以及到最后更新的参考资料都是一次付费后续免费的。注意：（建议先下单占坑，因为随着后续我们更新资料数据的增多，会进行相应价格的提升！！！） 国一学长出品，定价稍高，请谅解！

持续更新到比赛结束，建议早点占坑享受早鸟优惠价。后续更新详细思路代码等相继出来后会涨至80!

质量非常高，一等奖水平！先到先得！具体可参考往期国赛、地区赛等资料，都是预定满，一票难求的！（https://mbd.pub/o/bread/mbd-ZJmYlZlq，https://mbd.pub/o/bread/mbd-ZJqalZxx，https://mbd.pub/o/bread/mbd-ZJqUlZ9p ，https://mbd.pub/o/bread/mbd-ZJmYl5du ）

已更新 B题45页高质量一等奖【完整成品论文】，国一团队出品

获取链接：https://mbd.pub/o/bread/mbd-ZpWWmJht

更新B题完整MATLAB配套求解代码+结果数据，可直接运行

已更新第三套 五一杯B题18页思路模型建立过程【内含代码】

已更新第二套 每问详细目标函数+约束条件+决策变量设置文档【15页纯数学符号+建模过程】

已更新  30页每问详细【思路分析+模型建立过程+算法代码求解】文档.





B题 未来新城背景下的交通需求规划与可达率问题

整体分析

问题1：小型交通网络的交通需求分配

• 目标：最大化期望可达率，即在任意一条路段出现故障时，从起点到终点的车辆到达率。
• 数学模型：线性规划（LP）或整数线性规划（ILP），目标函数是可达率的加权和，约束包括交通需求满足、路径选择数量限制和非负流量。

问题2：中等规模交通网络的交通需求分配

• 目标：同问题1，但考虑任意5条路段同时出现故障的情况。
• 数学模型：随机规划或鲁棒优化模型，需要考虑多种故障情况的组合，目标函数可能需要通过模拟来近似计算。

问题3：考虑路段容量限制的交通需求分配

• 目标：在满足路段容量限制条件下，最大化期望可达率。
• 数学模型：混合整数线性规划（MILP），在问题2的基础上加入路段容量限制作为额外的约束条件。

问题4：新路段建设的优化

• 目标：选择新建路段的方案以最大化改进后的网络在任意5条路段故障时的期望可达率。
• 数学模型：组合优化问题，可能需要使用图论中的算法来确定新路段的最佳位置，同时使用线性规划或动态规划来优化交通流量分配。

问题1分析与模型建立+代码求解

为了解决问题1，我们需要建立一个数学模型来优化交通需求的分配，以便在任意一条路段发生突发状况时，网络中所有交通需求的期望可达率最大。以下是详细的分析和数学模型的建立：

符号定义

数学模型建立

4. 求解算法1

4. 求解算法2

代码

# 问题1的算法设计
def traffic_demand_allocation(demands, network):  
    # 步骤1：预处理数据
    paths = find_all_paths(network)
    .............
    # 步骤2：建立MILP模型
    model = create_milp_model(demands, paths)
    ...............详见付费内容
    # 步骤3：求解MILP模型
    solution = milp_solver(model)
    
    # 步骤4：结果分析
    if solution.is_feasible():
        path_allocation = analyze_solution(solution, paths)
        expected_accessibility = calculate_expected_accessibility(path_allocation, network)
    
    # 步骤5：后处理与报告
    report = generate_report(path_allocation, expected_accessibility)
    return report
 ........................ ...............详见付费内容
# 辅助函数的实现将依赖于具体的数学建模库和MILP求解器。


 ...............详见付费内容

问题2分析与模型建立+代码求解

为了解决题目2，我们首先需要理解问题背景和要求，然后建立一个数学模型来优化交通需求的分配。题目2要求我们在一个更大的交通网络中进行规划，同时考虑到任意5条路段出现突发状况时的期望可达率。

1. 问题描述

在图3所示的交通网络中，我们需要为每对起点和终点之间的交通需求分配路径，使得在任意5条路段出现突发状况时，网络中所有交通需求的期望可达率最大。

2. 符号定义

N：网络中的节点集合

· A：网络中的路段（边）集合

· dij​：起点 i 到终点 j 的交通需求

· xa​：路段 a 上的交通流量

· ya​：路段 a 是否出现突发状况的二元变量，ya​=1 表示路段 a 发生故障，ya​=0 表示路段 a 正常

· k：表示考虑的路段故障数量，题目中 k=5

启发式算法代码设计

1. 初始化：随机生成一组路径分配方案。

2. 迭代：在每次迭代中，随机选择一个起点-终点对，尝试重新分配它的路径以提高期望可达率。

3. 评估：计算当前方案的期望可达率。

4. 接受准则：如果新方案的期望可达率高于当前方案，接受新方案；否则，以一定的概率接受新方案（模拟退火策略）。

5. 终止：达到预定迭代次数或期望可达率在一定次数的迭代中没有显著提升时停止。

Python代码

import random

import numpy as np


# 假设我们有以下数据和函数：

# network: 交通网络的图表示

# demands: 每对起点终点的交通需求 {(i, j): demand}

# paths_between(i, j): 返回起点i到终点j的所有可能路径

# accessibility(paths, blocked_edges): 计算在某些路段blocked_edges被阻塞时的可达率
..........................省略部分见付费内容
 
def initialize_paths(demands, paths_between):

    path_allocation = {(i, j): random.choice(paths_between(i, j)) for i, j in demands}

    return path_allocation

 ................省略部分见付费内容

def calculate_expected_accessibility(path_allocation, network, demands):

    total_accessibility = 0

    num_paths = {(i, j): len(paths_between(i, j)) for i, j in demands}

    

    for edge in network.edges():

        blocked_accessibility = 0

        for (i, j), path in path_allocation.items():

            if edge in path and num_paths[(i, j)] > 1:  # 如果该路径被阻塞，且有其他路径可选

                blocked_accessibility += demands[(i, j)]

        total_accessibility += blocked_accessibility

    return total_accessibility

 

def propose_new_allocation(path_allocation, demands, paths_between):

    i, j = random.choice(list(demands.keys()))

    current_path = path_allocation[(i, j)]

    alternative_paths = paths_between(i, j) - {current_path}

    if alternative_paths:  # 如果有其他路径可选

        new_path = random.choice(list(alternative_paths))

        path_allocation[(i, j)] = new_path

    return path_allocation

 

def simulated_annealing(path_allocation, network, demands, paths_between, T0=1.0, alpha=0.99, max_iter=1000):

    current_accessibility = calculate_expected_accessibility(path_allocation, network, demands)

    best_accessibility = current_accessibility

    best_allocation = path_allocation

    

    for iteration in range(max_iter):

        T = T0 / (1 + iteration * alpha)  # 降温

        new_allocation = propose_new_allocation(path_allocation, demands, paths_between)

        new_accessibility = calculate_expected_accessibility(new_allocation, network, demands)

        

        # 接受准则

        if new_accessibility > current_accessibility:

            path_allocation = new_allocation

            current_accessibility = new_accessibility

        elif np.exp((current_accessibility - new_accessibility) / T) > random.random():

            path_allocation = new_allocation
..........................................省略部分见付费内容
        

        # 更新最佳解

        if current_accessibility > best_accessibility:

            best_accessibility = current_accessibility

            best_allocation = path_allocation

  ......................................省略部分见付费内容

    return best_allocation

问题3分析与模型建立+代码求解

问题4分析与模型建立+代码求解

为了解决问题4，我们需要建立一个数学模型来确定新修建路段的方案，以最大化在任意5条路段出现突发事故时的网络中所有交通需求的期望可达率，同时满足各路段上的交通量不超过路段容量的要求。

（6）路径规划交通量约束：

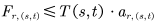
............详见付费内容