指数三角优化算法(Exponential-Trigonometric Optimization, ETO)是发表在中科院一区期刊“Computer Methods in Applied Mechanics and Engineering”的2024年智能优化算法
01.引言
指数三角优化算法(Exponential-Trigonometric Optimization,ETO) 算法是一种基于指数函数与三角函数融合的新型元启发式优化算法,专为复杂工程优化问题设计。该算法通过创新的数学机制平衡探索与开发阶段,引入约束搜索策略和动态转换机制,有效解决了传统算法易陷入局部最优、收敛速度慢等问题。ETO在CEC标准测试函数和压力容器设计、翼型优化等实际工程问题中展现出卓越性能,其核心创新点在于将指数衰减特性与三角函数周期性相结合,构建动态权重系数来指导搜索过程。
02.优化算法原理及流程(文末附代码)
算法原理
1.算法核心思想
ETO通过以下机制实现高效优化:
(1)指数-三角混合机制:利用指数函数的衰减特性和三角函数的周期性振荡,构建动态权重系数α₁、α₂、α₃,控制搜索步长。
(2)阶段转换机制:通过阈值T和转换系数CM动态切换探索与开发阶段,前期侧重全局搜索,后期增强局部挖掘。
(3)约束搜索策略:动态调整搜索空间边界,逐步缩小范围以提高收敛精度。
2.数学基础
- 权重系数计算:
alpha_1 = rand()*3*(t/Max_Iter-0.85)*exp(abs(d1/d2)-1); % 探索阶段权重
alpha_3 = rand()*3*(t/Max_Iter-0.85)*exp(abs(d1/d2)-1.3); % 开发阶段权重
alpha_2 = rand()*exp(tanh(1.5*(-t/Max_Iter-0.75) - rand())); % 第二阶段权重
- 阶段转换函数:
pCM = (sqrt(t/Max_Iter)^tan(d1/(d2)))*rand()*0.01; % 控制阶段转换
3.阶段划分
- 第一阶段(t ≤ T):全局探索为主,通过大范围随机扰动寻找潜在最优区域。
- 第二阶段(t > T):局部开发为主,围绕当前最优解精细搜索。
算法流程与代码解析
1. 初始化阶段
% 参数初始化
b = 1.55; CE = floor(1+(Max_Iter/b)); % 约束搜索周期
T = floor(1.2+Max_Iter/2.25); % 阶段切换阈值% 种群初始化
X = initialization(N, Dim, UB, LB); % 生成初始种群
Objective_values = Fobj(X); % 计算适应度
[Destination_fitness, idx] = min(Objective_values);
Destination_position = X(idx,:); % 全局最优解
2. 主循环流程
while t <= Max_Iter
for i = 1:N % 遍历每个个体
for j = 1:Dim % 遍历每个维度
% 计算动态参数d1/d2
d1 = 0.1*exp(-0.01*t)*cos(0.5*Max_Iter*(1 - t/Max_Iter));
d2 = -d1; % 对称参数 %
约束搜索策略激活
if t == CEi
UB_2 = ...; LB_2 = ...; % 动态调整边界
X = initialization(N,Dim,UB_2,LB_2); % 重新初始化种群
end
% 阶段判断与位置更新
if t <= T
if CM > 1 % 探索阶段
X(i,j) = ...; % 公式(8)
else % 开发阶段
X(i,j) = ...; % 公式(14)
end
else
if CM < 1 % 第二阶段开发
X(i,j) = ...; % 公式(16)
else % 第二阶段探索
X(i,j) = ...; % 公式(12)
end
end
end
end
% 适应度更新与排序
Objective_values = Fobj(X);
[~, sorted_idx] = sort(Objective_values);
Destination_position_second = X(sorted_idx(2),:); % 次优解
t = t + 1;
end
3.关键操作详解
动态边界调整:当迭代次数达到CEi时,根据当前最优解和次优解重新计算搜索边界,增强局部搜索能力。
UB_2 = Destination_position(j) + (1-t/Max_Iter)*abs(rand()*Destination_position(j)-...);
LB_2 = Destination_position(j) - (1-t/Max_Iter)*abs(rand()*Destination_position(j)-...);
- 位置更新策略:通过α系数控制移动幅度,tanh函数平滑过渡,exp函数调节衰减速度。
- 种群排序机制:每轮迭代后对种群排序,保留次优解用于后续边界计算。
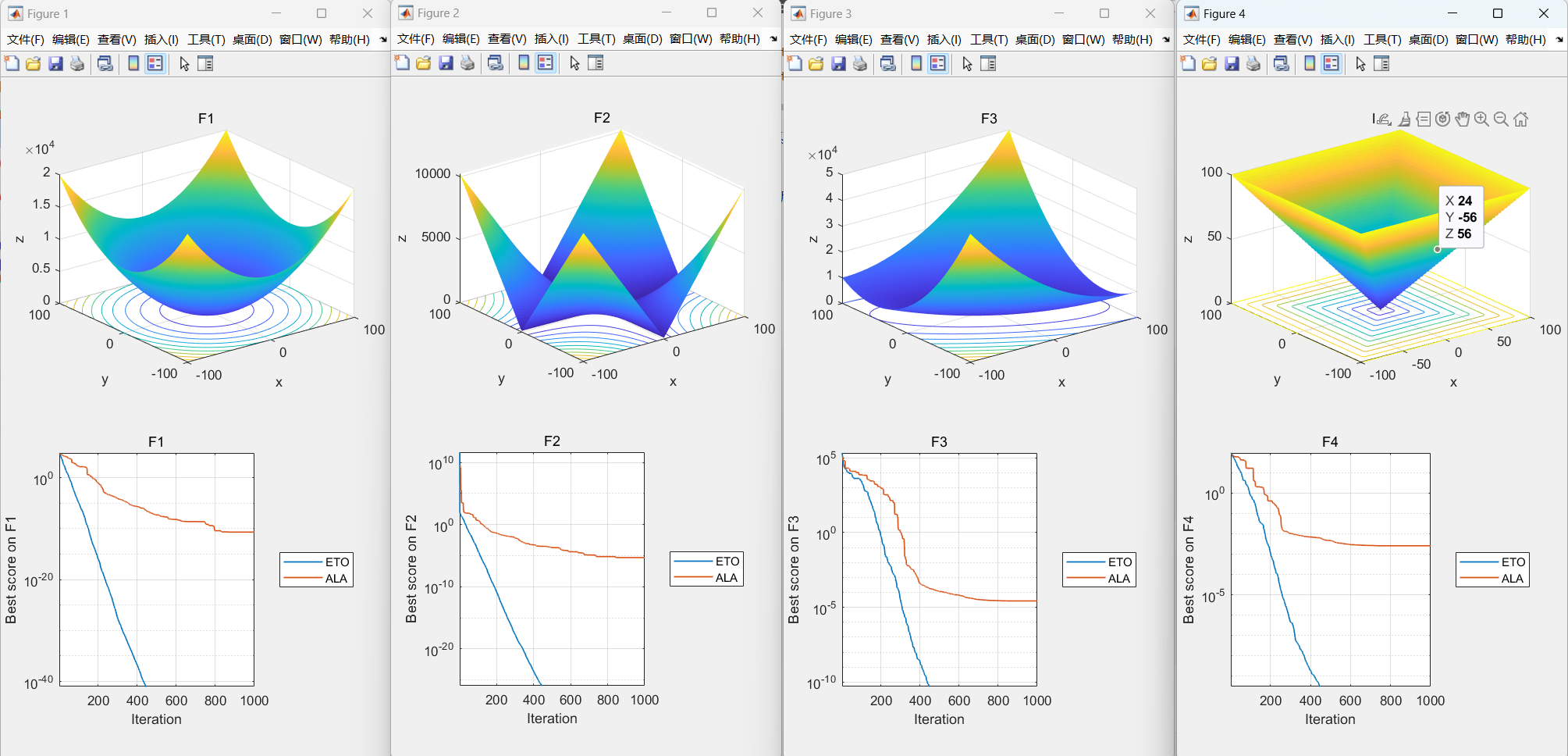
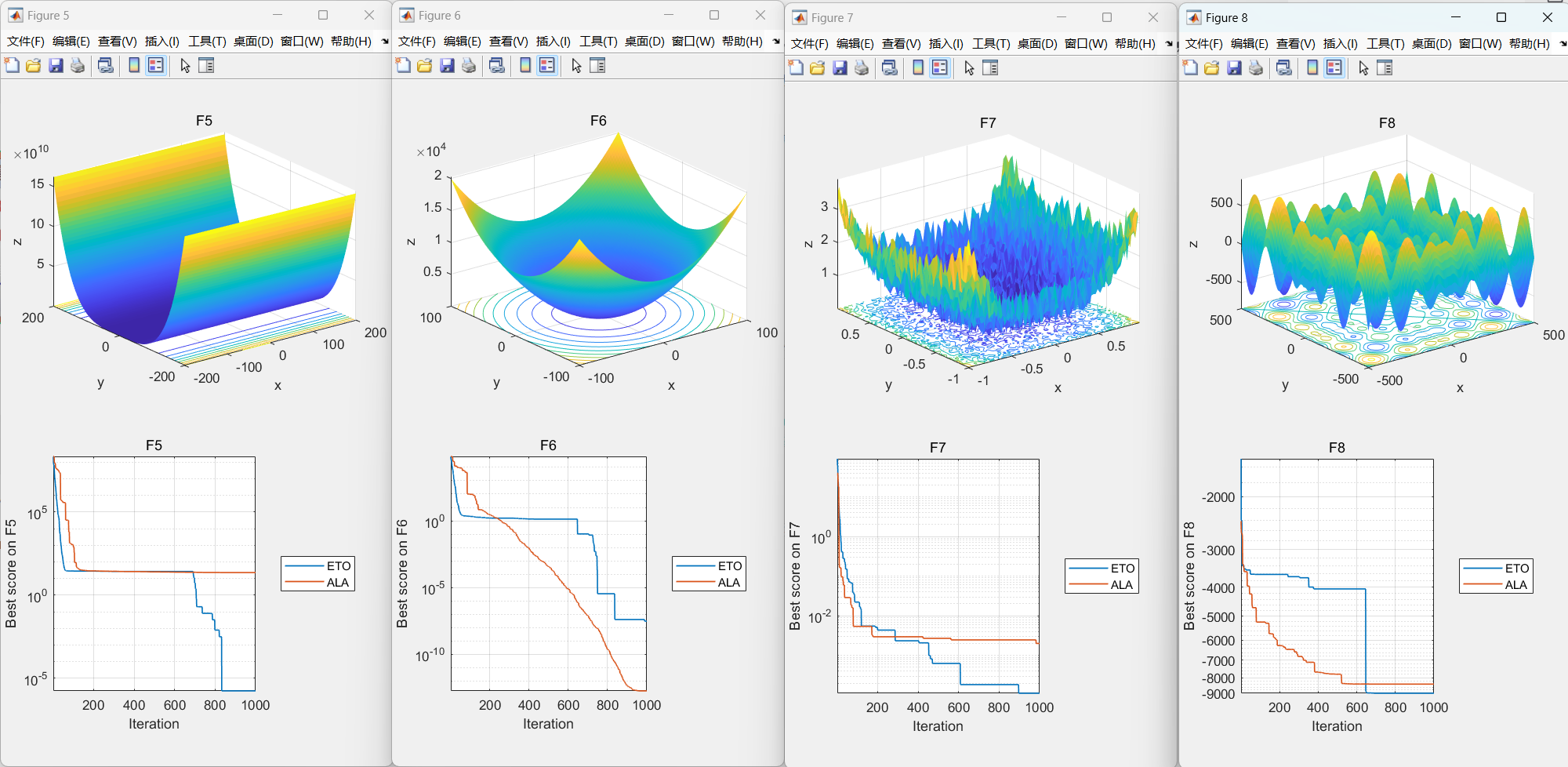
03优化算法测试函数效果图
✅作者简介:信号处理方向在校博士研究生,目前专研于MATLAB算法及科学绘图等,熟知各种信号分解算法、神经网络时序、回归和分类预测算法、数据拟合算法以及滤波算法。提供一个可以相互学习相互进步的平台
🚩技术信仰:知行合一,让每一行代码都成为解决问题的利器
🔍后台添加博主微信并备注个人需求(比如ETO-BP)定制以下ALA算法优化模型:
1.回归/时序/分类预测类:BP、RF、XGBoost、RBF、LSSVM、SVM、ELM、DELM、ESN、RELM等等均可,优化算法优化BP为例,可达到以下效果:
2.分解类:EEMD、VMD、REMD、CEEMDAN、ICEEMDAN、SVMD等分解模型均可,优化算法优化VMD/ICEEMDAN为例,可达到以下效果:
(2)基于改进天鹰优化算法(IAO)优化ICEEMDAN参数
3.去噪算法算法类:VMD/CEEMDAN/ICEEMDAN/SVMD+小波阈值/SVD去噪,可在去噪算法前加智能优化算法优化参数以VMD-WT/SVD为例,可达到以下效果:
关注"MATLAB科研小白"后联系博主私家定制