迭代自适应法 (Iterative Adaptive Approach,IAA)估计算法最早由美国的电气工程师和数学家Robert Schmidt和Roy A. Kuc在1986年的一篇论文"Multiple Emitter Location and Signal Parameter Estimation"中首次提出了这一算法, IAA DOA 估计算法是一种用于无线通信和雷达系统中估计信号到达方向的方法,对于信号处理和通信领域具有重要意义。
对于实际的雷达DOA估计来说,传统的延时相加方法(Delay-And-Sum, DAS)分辨率低,旁瓣干扰大。而ESPRIT2I和MUSIC等方法只有在传感器数大于源信号数,并且需要大量的快拍数,和高信噪比的情况下来获得高分辨率,但是在实际的工程应用中,收集大量的快拍是不切实际的,尤其是在快速的时变环境很难做到这一点,使得定位性能恶化。此外,由于对子空间正交性比较敏感,基于子空间的方法也不能处理相干源问题。
IAA是一种依赖数据,基于加权最小二乘方法(WLS)的非参数的迭代自适应算法,它可以在少量快拍(甚至是一个)、相干或非相千源、任意阵列的情况下得到很好的参数估计,相比于其他依赖于数据的方法,IAA可以大大地增加分辨率并且减小旁瓣,所以它的性能要比现有的空间稀疏信号重构算法好。
阵列信号经常遇到的问题是少量的快拍数和低信噪比。针对这个问题应用IAA算法就可以很好地减小这些不利因素对信号估计的影响。由于实际信号往往要比观测信号少得多,所以,将阵列信号处理问题转换到稀疏信号表示领域。因为稀疏信号表示方法可以处理少量快拍数的情况,甚至是一个。而这种基于稀疏表示的方法也被用在频谱估计、图像处理、阵列设计和其他很多领域。
IAA算法原理链接:
https://blog.csdn.net/Poulen/article/details/135296816
IAA算法代码:
IAA算法代码:
% IAA
% P = a'R^-1X/(a'R^-1a)
clc; clear; close all;
%% Initial signal
% IAA can work on one or more snapshots, this work just show one snapshot
T = 1;
snsrMap = [1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12];
tThetas = [5; 10];
[X, tA] = arrayModel(snsrMap, T, tThetas);
tS = pinv(tA' * tA) * tA' * X;
%% Initial scan grid
pThetas = -64:0.5:63.5;
pThetas = pThetas .';
pA = exp(1i * pi * (snsrMap - 1)* sind(pThetas).');
pA = pA ./ norm(pA(:, 1));
%% DBF
pDBF = zeros(size(pThetas));
for i = 1: length(pThetas)
pDBF(i) = pinv(pA(:, i)' * pA(:, i)) * pA(:, i)' * X(:, 1);
end
%% IAA
R = X * X' ./ T;
maxIter = 16;
P = diag(abs(pDBF).^2);
for i = 1: maxIter
Q = R - pA * P * pA';
invQ = pinv(Q);
aS = zeros(size(pThetas));
for j = 1: length(pThetas)
aS(j) = pA(:, j)' * invQ * X / (pA(:, j)' * invQ * pA(:, j));
end
figure(2);
plot(abs(aS));
P = diag(abs(aS) .^2);
end
%% Figure;
figure;
plot(pThetas, 20 * log10(abs(pDBF) / max(abs(pDBF))));
hold on;
plot(pThetas, 20 * log10(real(P) / max(real(P))));
for i = 1: length(tThetas)
xline(tThetas(i), '--g');
end
legend("DBF", "IAA", "Golden")
grid on;
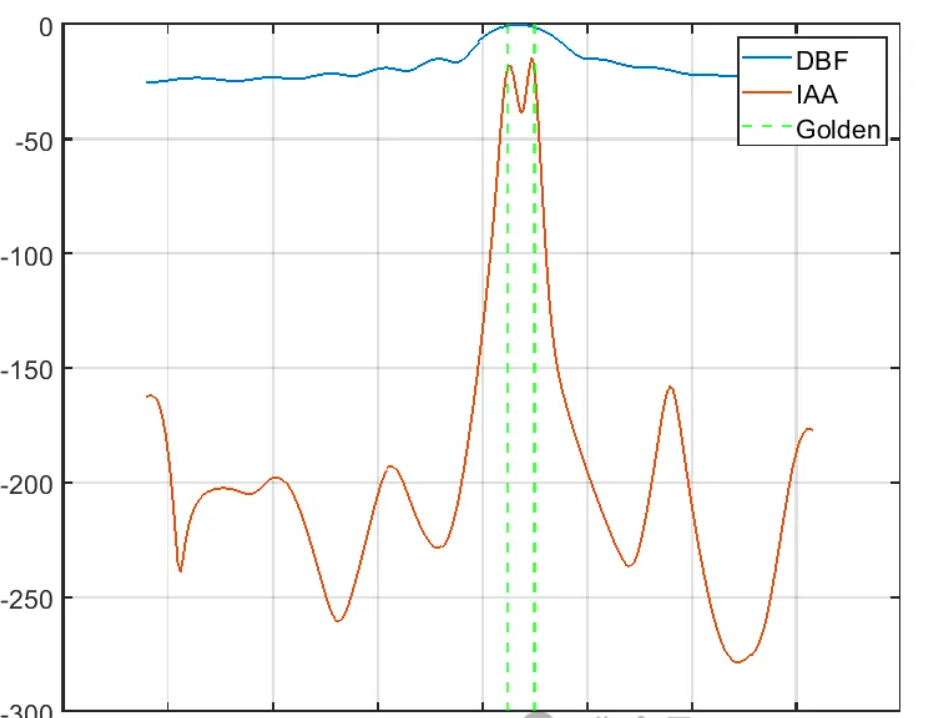
IAA仿真结果