模糊散布熵Fuzzy dispersion entropy 于2022发表在中科院1区SCI IEEE Transactions on Fuzzy Systems, 目前知道的人少，应用的文献更是少了，先用先发。

1. 自带测试数据，一键完美运行。更换数据简单方便。
2. 不提供代码讲解，代码售出不退，仅供参考学习，出现任何违反学术行为与本店无关。
3. 购买前，请您确认是否有matlab基础和阅读过相关文献

（本作品无下图，介意勿拍）

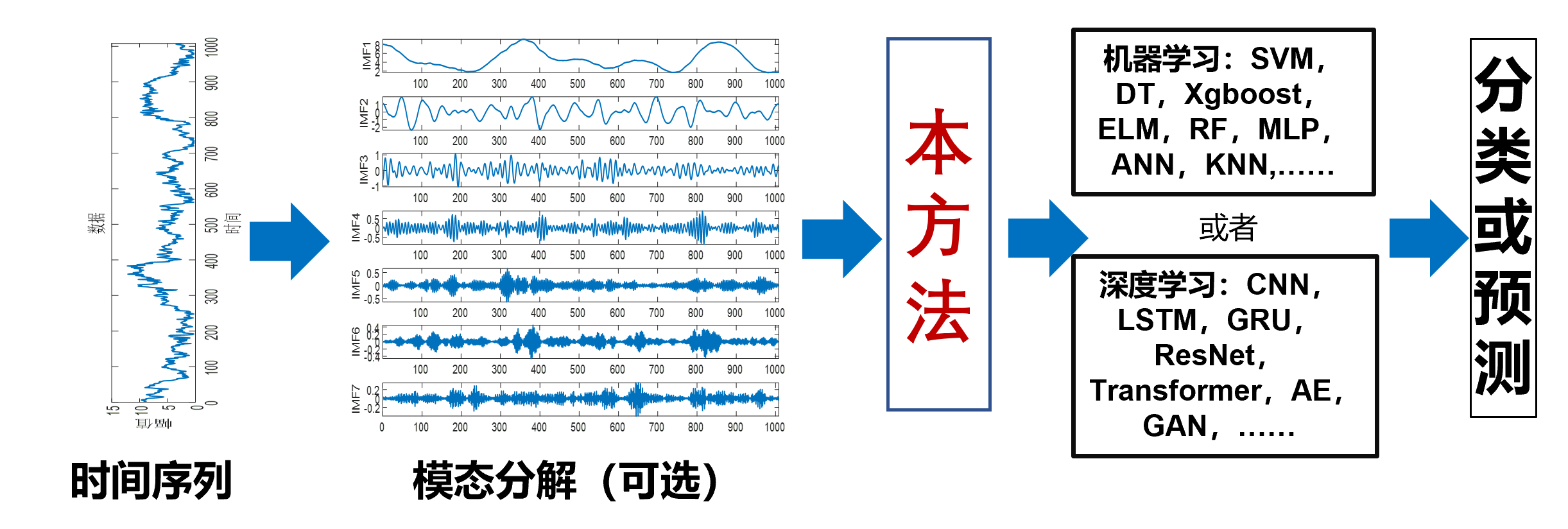
该算法非常简单，易于实现，作为特征提取方法可以与机器学习、深度学习结合，解决复杂的分类或预测问题，可用于生物医学、神经科学、电气、交通、气象、能源动力、水利、海洋科学、经济、土木、计算机科学、机械、工业工程等领域时间序列分析和特征提取。



参考文献：

[1] M. Rostaghi, M. M. Khatibi, M. R. Ashory, and H. Azami, “Fuzzy Dispersion Entropy: A Nonlinear Measure for Signal Analysis,” IEEE Transactions on Fuzzy Systems（一区）, vol. 30, no. 9, pp. 3785–3796, Sep. 2022, doi: 10.1109/TFUZZ.2021.3128957.

包括：

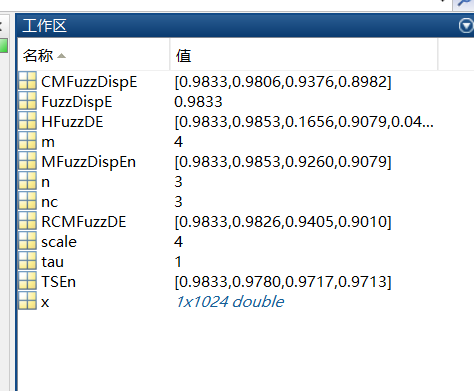
1.模糊散布熵（Fuzzy dispersion Entropy），

2.多尺度模糊散布熵（Multiscale Fuzzy dispersion Entropy），

3.复合多尺度模糊散布熵（composite multiscale Fuzzy dispersion entropy），

 4.精细复合多尺度模糊散布熵（refined composite multiscale Fuzzy dispersion entropy），

5.时移多尺度模糊散布熵（time-shift multiscale Fuzzy dispersion entropy），

6.层次模糊散布熵（Hierarchical Fuzzy dispersion entropy）