本文的主要参考文献:
Zeng B , Zhao L . Solving Two-stage Robust Optimization Problems by A Constraint-and-Column Generation Method[J]. Operations Research Letters, 2013, 41(5):457-461.
1.两阶段鲁棒优化问题的引入
鲁棒优化是应对数据不确定性的一种优化方法,但单阶段鲁棒优化过于保守。为了解决这一问题,引入了两阶段鲁棒优化(Two-stage Robust Optimization)以及更一般的多阶段鲁棒优化,其核心思想是将决策问题分为两个阶段。第一阶段是进行初步决策,第二阶段是根据第一阶段的决策结果制定更好的决策策略,应对数据不确定性的影响。这种方法可以降低保守性,提高鲁棒性。
假设一阶段和二阶段决策问题都是线性规划,并且不确定性集合U是一个有限的离散集合或者多面体集。使用y表示第一阶段决策变量,x表示第二阶段决策变量,表示不确定矢量。在此假设下的两阶段鲁棒优化的一般形式为:

其中:
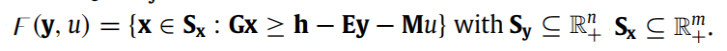
向量c,b,d,h和矩阵A , G , E , M都是确定性的数值,不确定性体现在向量u上。注意到第二阶段优化的约束条件F(y,u)是关于不确定性u的线性函数。
原文献中提供了以运输问题作为算例,具体如下:
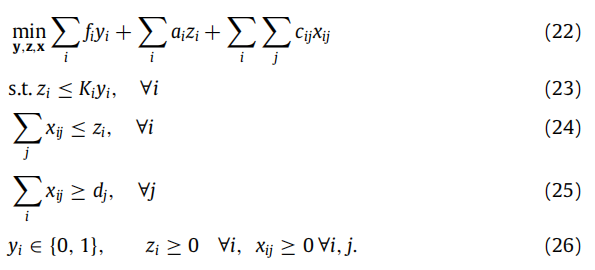
其中,yi为0-1变量,表示是否在i地建设仓库,zi表示仓库i储存的商品数量,xij表示从i仓库到j客户运送的商品数量,fi表示建设仓库i的固定成本,ai表示仓库i存储商品的单位成本,cij表示从i仓库到j客户运送单位商品的成本,ki表示仓库i的最大容量,dj表示客户j的需求。
不确定变量为客户的需求,表达方式如下:
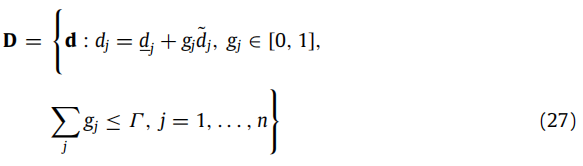
具体算例参数:

根据上面的公式,我们可以写出各个参数矩阵以及变量的表达式:
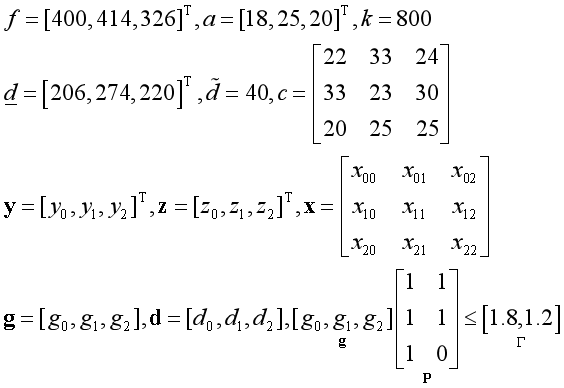
用matlab代码表示:
%% 参数矩阵
f = [400; 414; 326];
a = [18; 25; 20];
k = 800;
C = [22, 33, 24;
33, 23, 30;
20, 25, 27];
d_ = [206; 274; 220];
d_wave = 40;
gamma = [1.8,1.2];
P = [1 1;1 1;1 0];
%% 决策变量
y = binvar(3,1);
z = sdpvar(3,1);
x = sdpvar(3,3,’full’);
d = sdpvar(3,1);
g = sdpvar(3,1);
可以尝试求解一下这个确定性优化问题,和后面的两阶段鲁棒优化进行对比:
%% 目标函数
objective = f'*y + a'*z + sum(sum(C.*x));
%% 约束条件
Constraints = [];
Constraints = [Constraints , z >= 0 , x >= 0 , g >= 0 , g <= 1];
Constraints = [Constraints , z <= k*y];
Constraints=[Constraints , sum(x) <= z'];
Constraints=[Constraints ,sum(x,2) >= d];
Constraints=[Constraints ,d == d_ + g*d_wave];
Constraints=[Constraints ,g'*P <= gamma];
%% 设置求解器
ops=sdpsettings('verbose', 3, 'solver', 'gurobi');
sol=optimize(Constraints,objective,ops);
优化结果为:
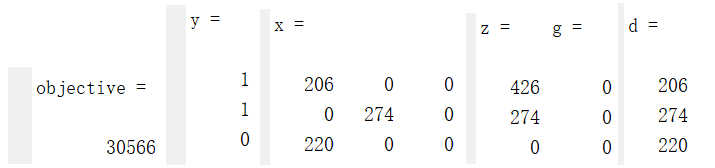
进一步把算例写成两阶段鲁棒优化的形式:
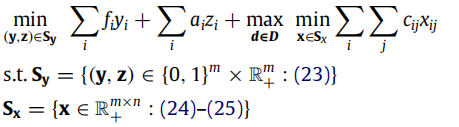
针对这个两阶段鲁棒优化问题,可以分别采用Benders对偶割平面法和C&CG算法进行求解。
2.Benders对偶割平面法
2.1基本原理
Benders对偶割平面法可以用于解决两阶段鲁棒优化问题,首先将两阶段鲁棒优化问题分解为两部分:主问题(Master Problem,MP)和子问题(Subproblem,SP)。主问题包含第一阶段的决策变量y以及仅与y有关的约束和子问题返回的割,还包括辅助变量η,用于评估第二阶段目标函数的取值。子问题包含第二阶段的决策变量x和不确定变量u,旨在给出第二阶段目标函数值的一个界限值。针对式(1)中描述的两阶段鲁棒优化问题,其主问题MP可以写成:
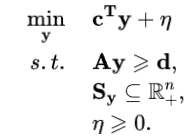
主问题是一个线性规划问题。子问题SP则为:
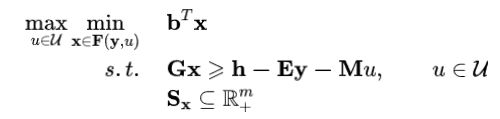
而子问题是一个双层线性规划问题(如果不知道双层规划的概念,可以去看看我之前的几篇博客双层优化入门-CSDN博客),其中上层优化的决策变量是u,下层优化的决策变量是x,而且在下层优化中,变量y和u的值都是确定的,可以视为参数。
对于双层优化形式的子问题的求解,主要有以下几种方式:
1.按原文献提供的方式,通过对偶变换将双层优化问题转为单层优化问题,再进行求解,可以使用智能优化算法、等价线性化、二次规划求解器(例如gurobi)等方式进行求解;
2.采用智能优化算法进行求解(可参考博客双层优化入门(3)—基于智能优化算法的求解方法);
3.采用KKT条件进行求解(可参考博客双层优化基本原理与求解方法、基于yalmip的双层优化求解)。
在这里我们使用KKT条件来求解子问题,可以将双层优化的子问题转换为下列单层优化的形式:
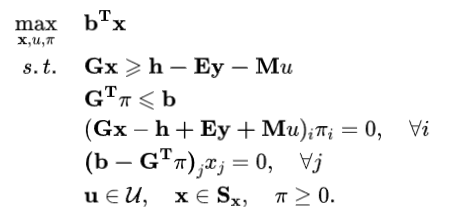
上面的约束存在非线性形式,可以使用大M法引入二进制中间变量进行线性化,将其转换为混合整数规划的形式:
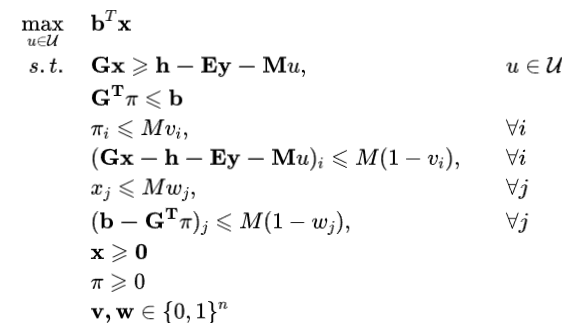
对于一般形式的两阶段鲁棒优化问题(如式(1)),Benders对偶切平面算法求解的流程如下:
步骤1:设定目标函数上界UB=+∞, 下界LB=-∞,迭代次数k=0。
步骤2:求解主问题MP:
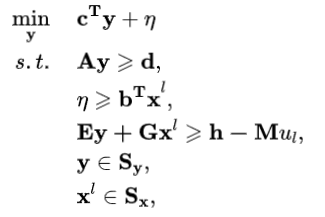
求出最优解(yk+1*,ηk+1*),并更新LB=max{LB,c T yk+1*+ηk+1*};
步骤3:求解子问题SP:
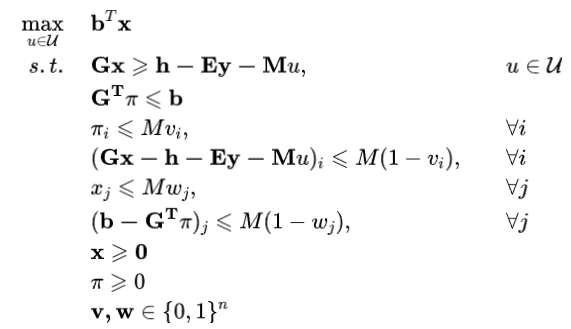
求出子问题的最优目标函数值Qk+1以及最优解(uk+1,xk+1*),并更新UB=min{UB,cT yk *+Q(yk*)}。
步骤4:如果UB-LB ≤ ε(事先设定的运行偏差),则输出优化结果,并退出循环。否则令k=k+1,将约束添加到主问题MP中并返回步骤2。
从上述步骤中可以看到,算法迭代的过程会不断向主问题添加约束条件,也就是割平面,因此被称为Benders对偶割平面法。
。。。。。