2023 国赛C题，高教社杯建模解析，小鹿学长带队指引全代码文章与思路

作品简介

小鹿学长来啦，我的目标是为广大建模爱好者提供深入和全面的数学建模资源，无论你是刚刚入门还是想进一步提高建模技能，我都可以提供一些建议呀。毕竟当年也是拿了国一的选手~~

小鹿学长联合20多位国二以上的好队友，共同提供了进阶版精华包呀，有兴趣的同学可以点击下面链接看看～～

link：（进阶版）2023 国赛C题，高教社杯建模解析，小鹿学长带队指引全代码文章与思路


在"小鹿学长"的世界中，你将会找到：

  1. 深刻的建模思路： "小鹿学长"会引导你深入理解数学建模的核心思想。他将教你如何将复杂的现实问题转化为数学模型，以及如何选择适当的数学工具来解决这些问题。这将帮助你在面对各种挑战时保持冷静和创造性。
  2. 精心编写的文章： 他的文章是深入且易于理解的。你将从中学到问题陈述、模型构建、参数估计、模拟和结果解释等各个方面的技巧。这些文章不仅仅是教程，更是指导你如何应对实际问题的宝贵资源。
  3. 实用的代码示例： 除了理论知识，"小鹿学长"会分享充满实用性的代码示例，帮助你将理论应用到实践中。无论你使用的是哪种编程语言，你都能在他的账号中找到有关数学建模的代码示例和技巧。
  4. 问题解答和指导： 如果你在建模过程中遇到问题，"小鹿学长"会及时回答你的疑问，并提供专业的建议。他的目标是确保你在建模项目中获得支持和帮助。

我已经把国赛C题呈现上来啦~有什么具体的想法也欢迎多交流！​

 我是小鹿学长，就读于上海交通大学，截至目前已经帮200+人完成了建模与思路的构建的处理了～

相信这回也能给大家一个非常好的帮助！！！

比赛的时候常规的数据分析办法 以及线性规划算法，一般来说在比赛中会经常考到～

所以要多多复习呀！

​编辑

问题一

  1. 销售量分布规律：首先，对于每个蔬菜品类，计算其销售量的平均值、方差、中位数等统计指标，以了解销售量的分布特点。这有助于确定销售量的稳定性和波动性。
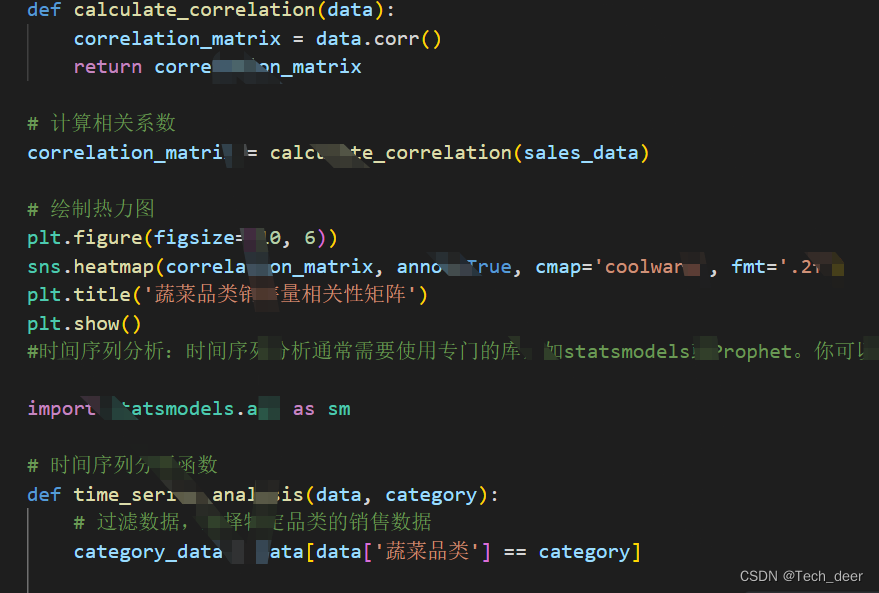
  2. 相关性分析：通过计算不同蔬菜品类之间的相关系数，可以确定它们之间是否存在相关性。正相关表示一种蔬菜的销售增加可能会导致另一种蔬菜销售增加，负相关表示相反情况，而无关系表示它们之间没有明显的关联。相关性分析可以帮助商超优化销售组合。
  3. 时间序列分析：对销售数据进行时间序列分析，可以检测销售量的季节性和趋势性变化。这有助于预测未来销售趋势，特别是在不同季节或假日期间。
  4. 特殊事件分析：查看销售数据是否受到特殊事件（例如促销、供应问题或天气影响）的影响。这些事件可能会导致销售波动，因此需要考虑它们。

具体来说：

相关性分析：

在进行相关性分析时，可以使用Pearson相关系数来度量不同蔬菜品类之间的线性关联程度。具体步骤如下：

  1. 计算相关系数：对于每对蔬菜品类，计算它们的Pearson相关系数。这可以通过公式计算：
  2. 相关系数​= \frac{\sum{(X_i - \bar{X})(Y_i - \bar{Y})}}{\sqrt{\sum{(X_i - \bar{X})^2} \sum{(Y_i - \bar{Y})^2}}}
  3. 其中，$X_i$和$Y_i$分别表示两个品类在不同时间点的销售量，$\bar{X}$和$\bar{Y}$分别表示两个品类销售量的平均值。
  4. 解释相关系数：相关系数的取值范围在-1到1之间。正相关系数接近1表示两个品类之间存在正向线性关系，即一个品类销售增加时，另一个品类销售也增加。负相关系数接近-1表示负向线性关系，而接近0表示两个品类之间没有线性关系。

时间序列分析：

时间序列分析可以使用ARIMA（Autoregressive Integrated Moving Average）模型，这是一种常用于预测时间序列数据的统计方法。步骤如下：

  1. 数据平稳性检验：首先，对销售数据进行检验，确保数据是平稳的。可以使用单位根检验（Augmented Dickey-Fuller测试）来判断是否需要进行差分操作以达到平稳性。
  2. 模型拟合：根据平稳的时间序列数据，使用ARIMA模型来拟合销售量的趋势、季节性和残差。ARIMA模型的参数通常是p（自回归阶数）、d（差分阶数）和q（移动平均阶数），这些参数可以通过观察自相关函数（ACF）和偏自相关函数（PACF）来确定。
  3. 模型评估：拟合模型后，使用历史数据进行模型的验证和评估，可以计算模型的预测误差（如均方根误差RMSE）来评估模型的准确性。
  4. 未来销售预测：使用拟合好的ARIMA模型对未来时间点的销售量进行预测，这可以帮助商超更好地计划补货。

​编辑

问题二

建模思路：

  1. 销售总量与成本加成定价的关系：首先，我们需要了解不同蔬菜品类的销售总量与其成本加成定价之间的关系。这可以帮助我们确定哪些品类的销售量高，哪些品类的成本加成定价效果好。
  2. 日补货总量和定价策略：基于销售总量和成本加成定价的关系，我们可以制定每个蔬菜品类的日补货总量和定价策略，以最大化商超的收益。这需要考虑销售波动、成本、品相变差等因素。
  3. 数学建模：我们可以使用数学建模来优化补货量和定价策略，以使商超的总收益最大化。这可能涉及到线性规划、优化算法或其他数学方法。

问题求解：

  1. 成本加成定价相关变量：
  • Pi​：品类 i 的成本加成定价。
  • Ci​：品类 i 的成本。
  • Qi​：品类 i 的补货总量。
  1. 销售相关变量：
  • Si​：品类 i 的销售总量。
  • Ri​：品类 i 的销售总收入。
  1. 总收益：
  • T：商超的总收益。
  1. 需求和市场相关变量：
  • Di​：品类 i 的市场需求量。
  1. 约束条件相关变量：
  • Li​：品类 i 的最小补货量。
  • Ui​：品类 i 的最大补货量。
  1. 其他参数和变量：
  • n：蔬菜品类的总数。
  • j：品类的索引（j=1,2,…,n）。

基于上述表示，你可以重新构建问题二的公式：

销售总量与成本加成定价关系：

Ri​=Si​⋅Pi​

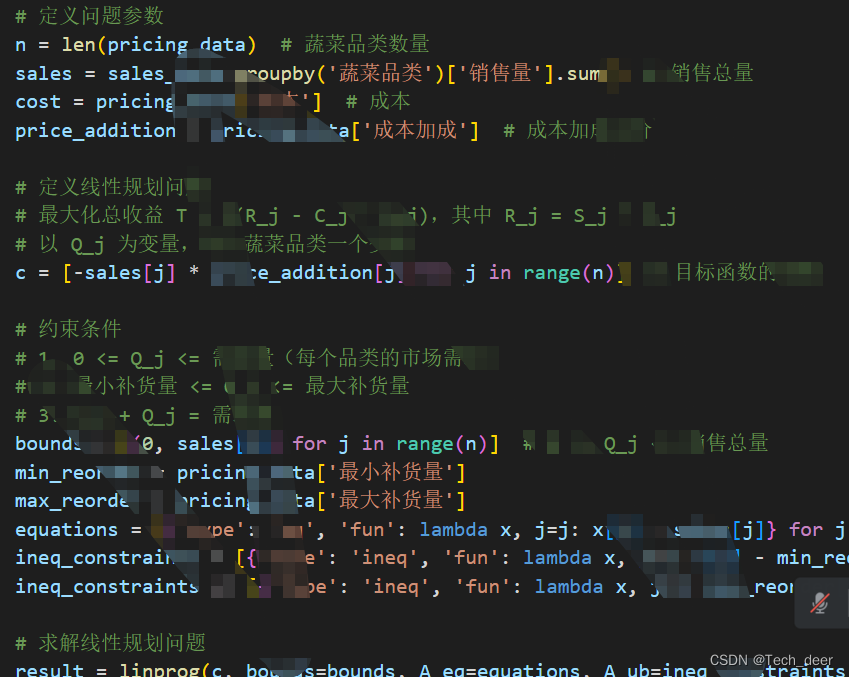
日补货总量和定价策略（优化问题）：

最大化总收益 T，其中：

T = \sum_{j=1}^{n} (R_j - C_j \cdot Q_j)

约束条件包括：

L_j \leq Q_j \leq U_j \quad \text{for } j = 1, 2,\ldots, n

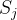
S_j + Q_j = D_j \quad \text{for } j = 1, 2, \ldots, n

​编辑

问题三

  1. 可售单品的选择：
  • 基于历史销售数据，计算每个单品的销售量和销售额。
  • 对单品进行排名，选择销售量和销售额最高的前33个单品（或根据具体要求选择数量）。
  • 确保所选单品的销售量满足市场需求。
  1. 补货计划和定价策略：
  • 对于每个可售单品，制定补货计划，以满足市场需求。这可以通过考虑历史销售趋势、市场需求波动性和销售季节性来实现。
  • 对于每个可售单品，制定定价策略，以最大化总收益。定价策略可以基于成本加成定价、市场需求弹性或其他定价模型。
  • 考虑商品的质量、品相、损耗率以及竞争对手的定价策略。
  1. 数学建模：
  • 使用整数规划（Integer Programming）或混合整数规划（Mixed Integer Programming，MIP）来建立数学模型。
  • 定义决策变量：
  • xi​：单品 i 是否选中销售，如果选中则为1，否则为0。
  • qi​：单品 i 的补货量。
  • pi​：单品 i 的定价。
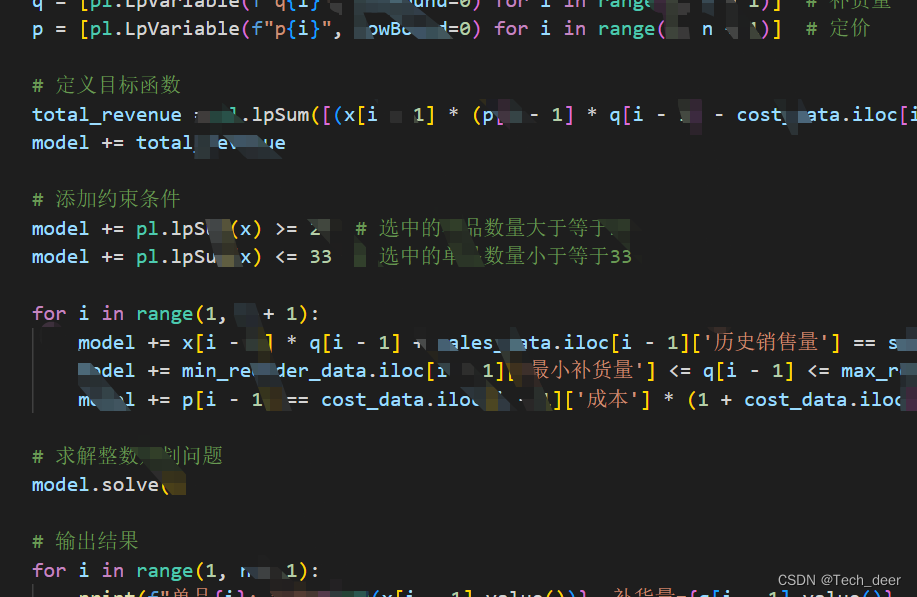
  • 定义目标函数：
  • 最大化商超的总收益 �T，其中 �T 可以表示为销售收入减去成本和损耗成本。
  • 目标函数可以表示为：T = \sum_{i=1}^{n} (x_i \cdot (p_i \cdot q_i - \cdot q_i - cdot q_i))
  • 约束条件包括：
  • 确保选中的单品数量在27-33个之间：\sum_{i=1}^{n} x_i \geq 27和\sum_{i=1}^{n} x_i \leq 33
  • 每个单品的销售量与补货量之和等于市场需求：x_i \cdot q_i + i =i \quad \text{for each } i
  • 补货量必须大于等于最小补货量，小于等于最大补货量：最小补货量i​≤qi​≤最大补货量i​（对于每个单品 i）
  • 定价策略的约束条件（例如，成本加成定价策略）：pi=成本⋅(1+加成比例)pi​=成本⋅(1+加成比例)（对于每个单品 i）
  1. 求解数学模型：
  • 使用数学优化工具（如PuLP、Gurobi、CPLEX等）来求解整数规划问题，找到最佳的补货计划和定价策略。
  • 获得最优解后，确定每个单品的补货量和定价策略，以满足市场需求并最大化商超的总收益。


​

创作时间：