C题：蔬菜类商品的自动定价与补货决策

题目回顾

在生鲜商超中，一般蔬菜类商品的保鲜期都比较短，且品相随销售时间的增加而变差，

大部分品种如当日未售出，隔日就无法再售。因此，商超通常会根据各商品的历史销售和需求情况每天进行补货。由于商超销售的蔬菜品种众多、产地不尽相同，而蔬菜的进货交易时间通常在凌晨 3:00-4:00，为此商家须在不确切知道具体单品和进货价格的情况下，做出当日各蔬菜品类的补货 决策。蔬菜的定价一般采用“成本加成定价”方法，商超对运损和品相变差的商品通常进行 打折销售。可靠的市场需求分析，对补货决策和定价决策尤为重要。从需求侧来看，蔬菜类 商品的销售量与时间往往存在一定的关联关系；从供给侧来看，蔬菜的供应品种在 4 月至 10 月较为丰富，商超销售空间的限制使得合理的销售组合变得极为重要。

赛题分析

该题针对超市中蔬菜类商品的销售实际情况进行分析。由于蔬菜类商品保质期短,超市需要制定合理的补货和定价策略,建立销量与价格之间的关系模型,并进行收益最大化的优化决策，以减少损耗。

本题重点关注以下四方面：

1. 分析蔬菜品类及单品之间的销量分布规律和关联关系。
2. 分析销量与价格的关系,给出单一周期的日补货量和定价策略,以最大化收益。
3. 在空间和最小陈列量约束下,确定单品的补货量和定价,以满足市场需求并最大化收益。
4. 自行查阅资料并分析如何以建立更准确的决策模型

解题思路

一、分析蔬菜各品类及单品销售量的分布规律及相互关系

1. 载入数据并搭载标记。
2. 对销售数据进行预处理,提取出日期、品类、单品和销售量。
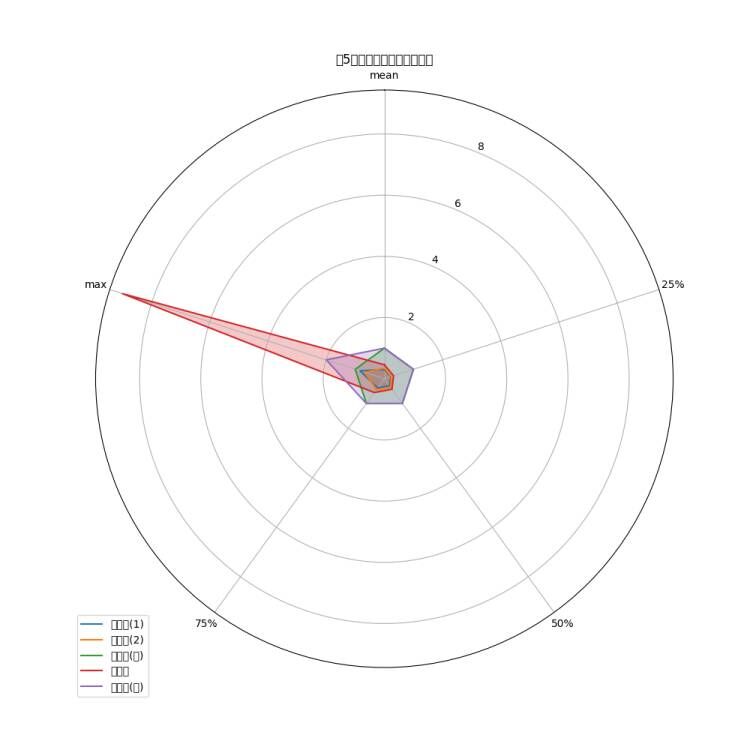
3. 可视化不同品类之间的销售规律,看是否存在关联。
4. 可视化不同单品之间的销售规律,看是否存在关联。
5. 采用相关性分析等方法,量化不同品类和单品之间的关联程度。

可视化建议如下：

1. 时间序列法分析不同品类和单品的销售量时间序列,直观地反应出它们之间的关联性。
2. 相关性分析法计算不同品类的销售量之间的相关系数矩阵,定量地描述它们之间的关联程度。

参考代码如下：

# 导入需要的模块
import pandas as pd
from datetime import datetime

# 读取三个Excel表格
data1 = pd.read_excel('附件1.xlsx') 
data2 = pd.read_excel('附件2.xlsx')
data3 = pd.read_excel('附件3.xlsx')

# 转换销售日期为 datetime 格式
data2['销售日期'] = pd.to_datetime(data2['销售日期'])

# 合并三个表格
data = pd.merge(data2, data1, on='单品编码') 
data = pd.merge(data, data3, on=['日期','单品编码'])

# 设置日期为索引
data = data.set_index('销售日期') 

# 绘制单品销量时间序列
data.groupby('单品名称')['销量'].sum().plot()

# 相关性分析
data.pivot_table(index=data.index, columns='单品名称', values='销量').corr()

# 导入库
import pandas as pd
from datetime import datetime
import matplotlib.pyplot as plt
import seaborn as sns

# 读取Excel
data1 = pd.read_excel('附件1.xlsx')  
data2 = pd.read_excel('附件2.xlsx')
data3 = pd.read_excel('附件3.xlsx')

# 处理数据
data2['销售日期'] = pd.to_datetime(data2['销售日期'])
data = pd.merge(data2, data1, on='单品编码')  
data = pd.merge(data, data3, on=['日期','单品编码'])

# 设置索引
data = data.set_index('销售日期') 
# ============== 时间序列图 ==============

# 1. 每个单品的销量时间序列折线图
（详见付费内容）

# 2. 每个分类的销量时间序列折线图  
（详见付费内容）

# 3. 热力图显示时间和单品的相关性
plt.figure()
data.pivot(columns='单品名称', values='销量').corr(method='spearman').plot(kind='heatmap')

# ============== 相关性分析图 ==============

# 4. 分类之间的相关性热力图
（详见付费内容）
# 5. 单品之间的相关性热力图
（详见付费内容）

二、制定蔬菜品类的补货计划和定价策略,最大化商超收益

1. 分析不同品类之间的销量关系,参考第一题的分析结果。
2. 建立销量和价格之间的关系,可以采用线性回归等方法。
3. 优化模型,给定成本约束,求解最大收益对应的价格和补货量。
4. 预测未来一周每日每个品类的销量。
5. 根据预测结果,计算出每个品类每日的补货量。
6. 在成本约束下,求出每个品类最优的价格。

编程思路如下：

1. 利用线性回归理论展现价格和销量之间的线性关系,预测不同价格下的销量。
2. 将优化理论中的目标函数设定为收益,约束条件为成本，调整价格,使收益最大化。

通过这两个模型的结合,求解出在成本约束下,达到最大收益的价格

参考程序如下：

# 建立线性回归模型
（详见付费内容）

# 根据模型预测销量
def predict_sales(category, price, coef):
    a, b = coef
    return a*price + b

# 求解最大收益对应的价格
from scipy.optimize import minimize
def get_optimal_price(category, coef, cost):
    def objective(p):
        sales = predict_sales(category, p, coef)
        return sales * p - sales * cost
    res = minimize(objective, 5)
    return res.x[0]

# 循环计算每个品类的最优价格
（详见付费内容）
    
# 预测未来一周的销量
predict_data = ... 

# 根据预测结果计算补货量  
replenish = {}
for date in predict_data:
    for c in predict_data[date]:
        replenish[(date,c)] = predict_data[date][c]

三、满足市场对各品类蔬菜商品需求的前提下,使得收益最大化

1. 分析不同单品间的销量关系,参考第一题结果。
2. 建立单品价格和销量之间的关系,可以使用线性回归。
3. 优化模型,添加限制可售单品总数和最小订购量约束。求解最大收益时的价格和订购量。
4. 预测每日每个单品的销量。
5. 计算满足约束的单品组合和对应补货量。
6. 在成本约束下,求出每个单品对应的最优价格

参考代码如下：

# 单品层面线性回归
（详见付费内容）
# 单品优化
from scipy.optimize import minimize  
def optimize_item(item, coef, cost):
    def objective(p):
        sales = predict_sales(item, p, coef)
        return sales * p - sales * cost
    res = minimize(objective, 5)
    return res.x[0]

# 添加限制条件求解
（详见付费内容）

# 处理优化结果得到价格和补货量
prices = res.x[:len(items)]
replenish = res.x[len(items):]

四、自行收集要素，完善模型评估体系

本项目的目的是为商超制定更佳的蔬菜商品补货与定价决策,提供一个可靠的销量预测模型。鉴于前三题分析所基于的数据仅考虑了日期、品类、单品、销量、价格等有限因素,导致预测结果存在一定偏差。因此,我们拟收集更多影响销量的关键数据,以提高预测的准确性和决策的可行性。

通过查阅相关文献,我们发现影响蔬菜销量的关键因素还包括季节性、气候条件、节假日、促销活动、客户需求和商品属性等(Wang et al., 2020; Lee and Park, 2018; Janssen et al., 2017)。具体而言:

1. 不同季节的销量数据。蔬菜种类和产量在春夏秋冬变化巨大,应收集不同季节的销量作为时间序列,建立季节性回归模型。
2. 气候数据,如温度、湿度、日照等。气候直接影响作物生长和产量,相关研究发现气温是预测蔬菜价格的重要变量(Asche et al., 2015)。
3. 节假日销量。节假日对蔬菜类商品需求量存在明显的周期性波动。应识别各类节假日,建立对应的假日样本。
4. 促销活动销量。针对特定蔬菜的促销会增加销量,应收集促销期间的销售数据。
5. 顾客数据,包括人口统计数据及购买习惯。不同人群的需求存在差异,应作为协变量加入模型。
6. 商品属性,如产地、种类、大小、包装和品质。这些因素会影响客户的购买决策。

综上,应计划扩大数据集范围,收集更加全面的影响因素数据,建立考虑多方面变量的销量预测模型,以提高补货和定价决策的精确度,使商超收益最大化。