KAN作为这两年最新提出的机制，目前很少人用，很适合作为预测的创新点，可以结合常规的网络加上个优化方法做创新。KAN（Kolmogorov–Arnold Networks）的模型，它对标的是MLPs（多层感知机），这个模型由数学定理Kolmogorov–Arnold启发得出的。该模型最重要的一点就是把激活函数放在了权重上，也就是在权重上应用可学习的激活函数，这些一维激活函数被参数化为样条曲线，从而使得网络能够以一种更灵活、更接近Kolmogorov-Arnold 表示定理的方式来处理和学习输入数据的复杂关系。

KAN通过将可学习的单变量函数置于网络边上，结合Kolmogorov-Arnold定理的数学保证，实现了高效高维函数逼近、参数效率与强可解释性统一、科学发现自动化，其突破性在于将神经网络从“黑盒”转变为“白盒”工具，为AI与科学计算的融合提供新范式。随着Wavelet-KAN、量子KAN等变体发展，KAN有望成为下一代深度学习基础架构。

代码主要功能

该MATLAB代码实现了一个基于Kolmogorov-Arnold Network (KAN) 的回归预测模型，核心功能包括：

1. 数据预处理：导入数据、划分训练/测试集、归一化处理

2. KAN模型训练：通过多项式函数逼近构建轻量级神经网络

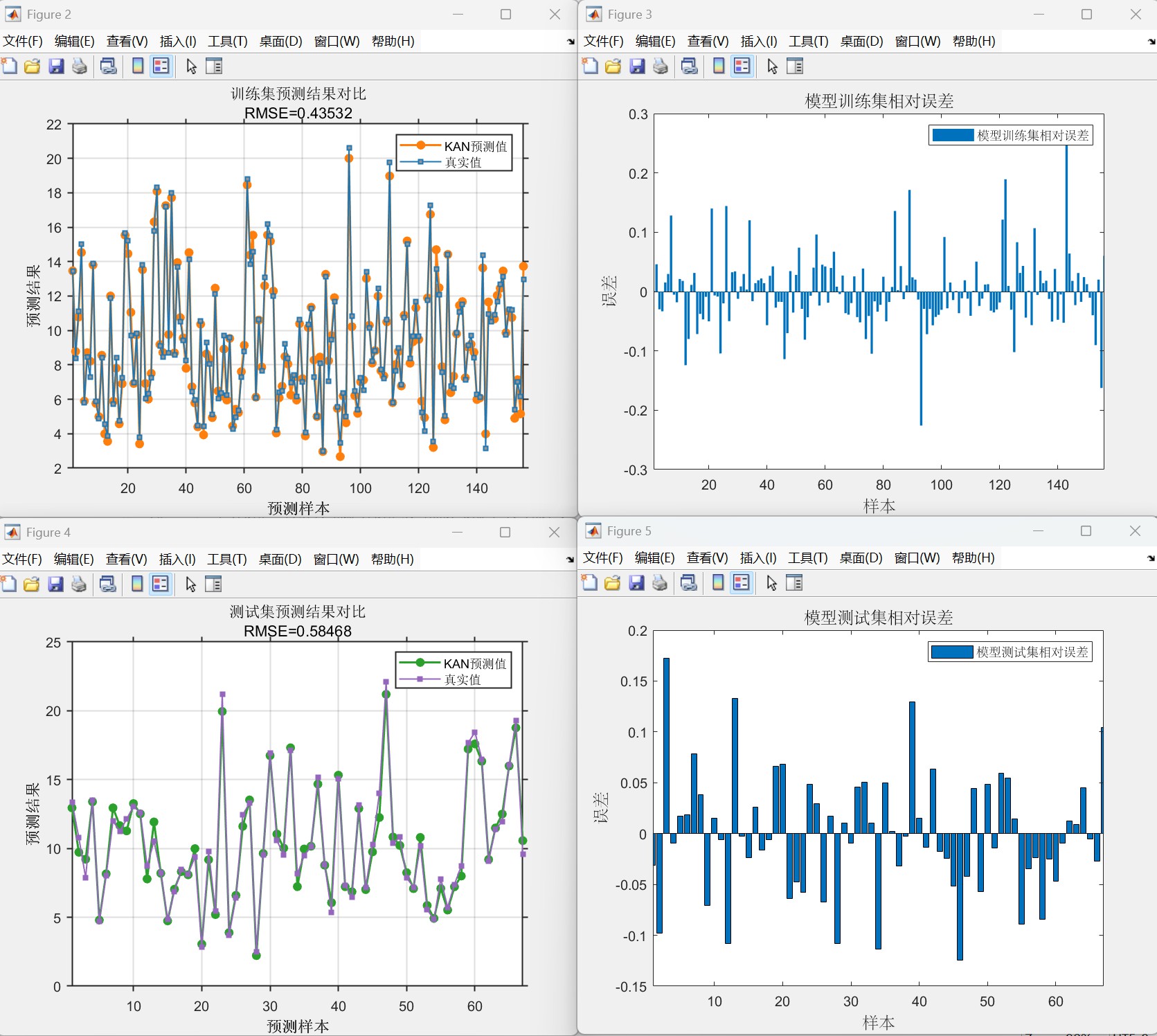
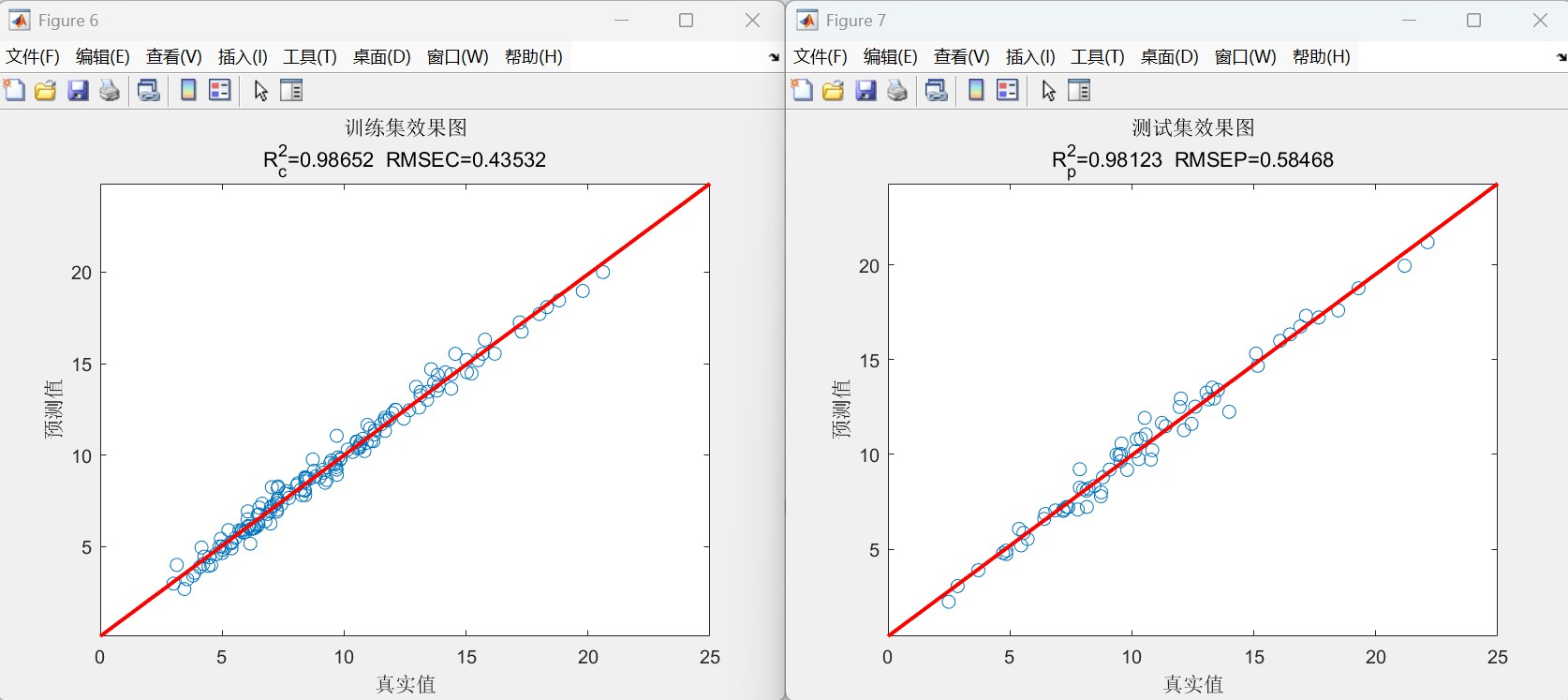
3. 预测与评估：输出回归预测结果，计算6大评估指标（R2、MAE、MAPE、MBE、MSE、RMSE）

4. 可视化分析：绘制预测对比图、误差分布图、线性拟合图

算法步骤

1. 初始化环境

• 清空变量/图窗/命令行，设置随机种子

2. 数据预处理

• 从Excel导入数据 (data.xlsx)

• 随机打乱数据集（可选）

• 按7:3划分训练/测试集

• 数据归一化到[0,1]区间 (mapminmax)

3. KAN模型构建

• 网络结构：输入层 → 多项式基函数层（φ） → 隐藏层 → 多项式基函数层（ψ） → 输出层

• 参数初始化：随机小数值初始化权重

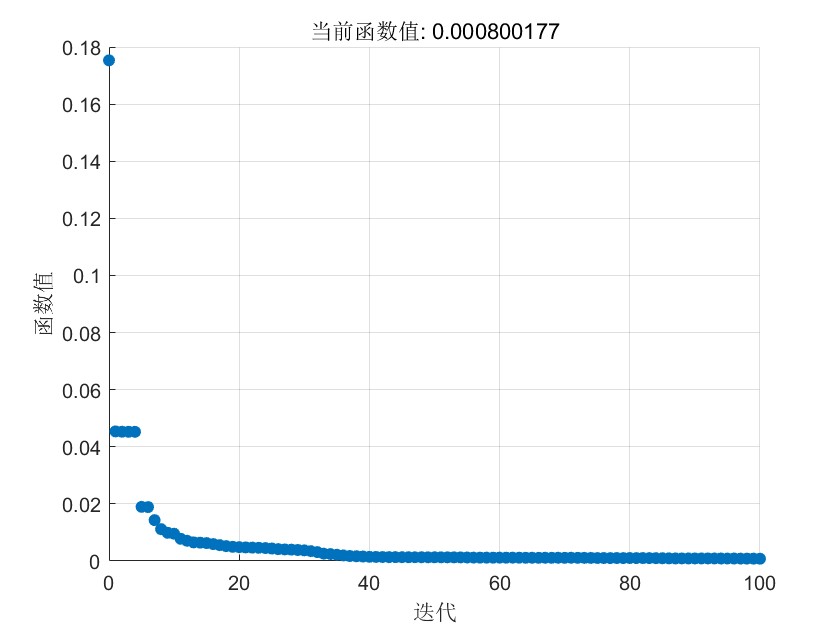
4. 模型训练

• 损失函数：均方误差 + L1/L2正则化项Loss = MSE + λ*L2 + α*L1

• 优化器：拟牛顿法 (fminunc)

5. 预测与反归一化

• 将预测结果还原到原始数据量纲

6. 性能评估

• 计算多个回归评价指标

• 绘制多类分析图表