粒子群优化算法是1995年发表在“Proceedings of ICNN'95 - International Conference on Neural Networks”的优化算法,至今直接引用3w+,是最经典的优化算法之一
01.引言
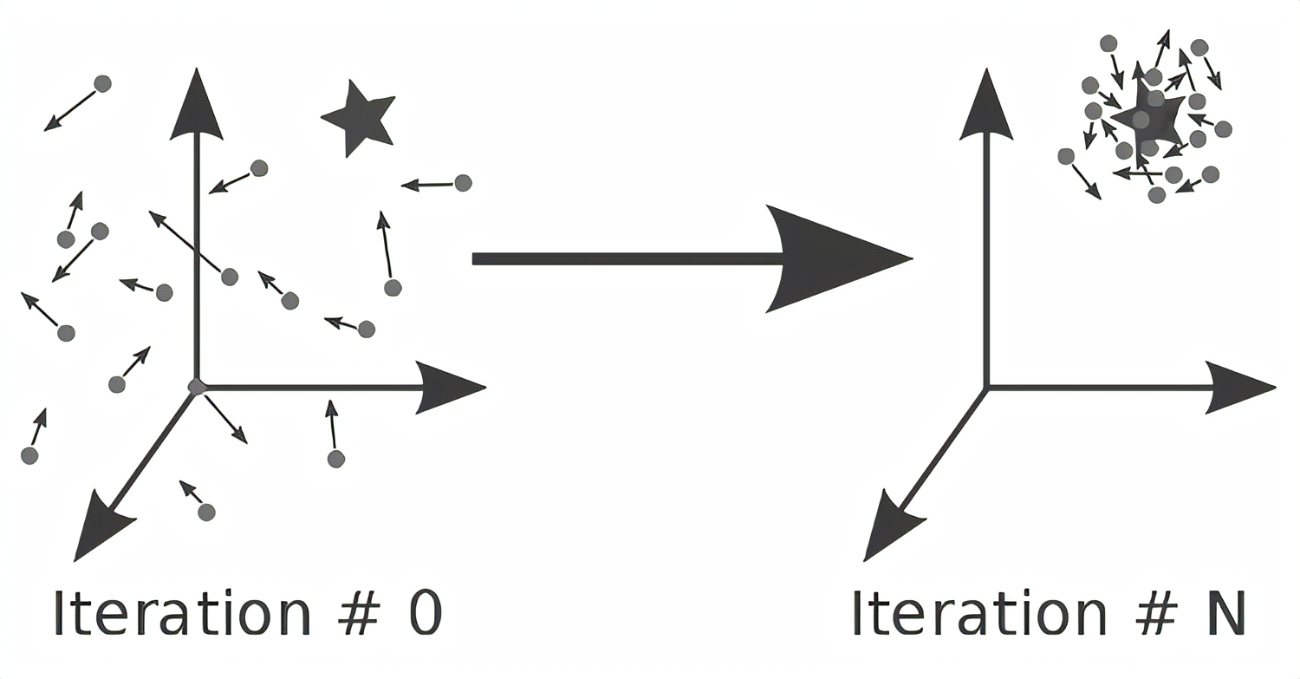
粒子群优化(Particle Swarm Optimization, PSO)由James Kennedy和Russell Eberhart于1995年提出,灵感源于鸟群、鱼群等群体行为的模拟。其核心思想是通过个体(粒子)间的社会信息共享(个体经验与群体经验)实现对非线性函数的优化。PSO结合了进化计算和群体智能的特点,具有以下优势:
1.简单性:仅需位置、速度、个体最优和全局最优(四个核心变量)。
2.低计算成本:无需复杂数学运算,适用于高维优化问题。
3.广泛适用性:成功应用于神经网络训练、函数优化等领域。

02.结合代码的算法的流程(文末附代码)
1.初始化参数
% 参数定义
N = 粒子数量; iter = 迭代次数; dim = 变量维度;
lb/ub = 变量上下界; y = 目标函数;
Vmax = 0.15*(ub-lb); % 速度最大值约束
w = 0.85; c1 = 1.2; c2 = 1.2; % 惯性权重与加速因子
% 粒子位置初始化
pos = lb + rand(N,dim).*(ub-lb);
vel = zeros(N,dim); % 初始速度为0
pBest = pos; % 个体最优初始化
gBest = zeros(1,dim);
gBestScore = inf; % 全局最优适应度(最小化问题)
- 位置与速度初始化:粒子在解空间内随机分布,速度初始为0。
- 参数设置:惯性权重w控制历史速度的影响;c1和c2分别调节个体与群体经验的权重。
2. 迭代优化过程
for l = 1:iter
% 边界处理:超出边界的粒子位置被拉回边界
pos = max(min(pos,ub), lb);
% 适应度计算与最优更新
for i = 1:N
fitness = y(pos(i,:));
if fitness < pBestScore(i)
pBest(i,:) = pos(i,:); % 更新个体最优
end
if fitness < gBestScore
gBest = pos(i,:); % 更新全局最优
end
end
% 速度与位置更新
for i = 1:N
vel(i,:) = w*vel(i,:) + c1*rand*(pBest(i,:)-pos(i,:)) + c2*rand*(gBest - pos(i,:));
vel(i,:) = min(max(vel(i,:), -Vmax), Vmax); % 速度限幅
pos(i,:) = pos(i,:) + vel(i,:);
end
cg_curve(l) = gBestScore; % 记录收敛曲线
end
- 边界处理:通过钳制位置确保搜索在可行域内(文档中提及的“避免碰撞”)。
- 适应度评估:计算目标函数值,更新个体与全局最优。
- 速度更新公式:
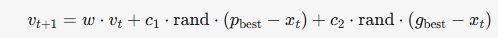
- 体现个体经验(c1项)与群体经验(c2项)的平衡。
3.收敛性分析
- 收敛曲线:cg_curve记录每次迭代的全局最优值,反映算法收敛速度与稳定性。
- 参数影响(文档中讨论):
- 高c1(个体倾向):粒子过度依赖自身经验,可能导致发散。
- 高c2(群体倾向):粒子过早收敛至局部最优。
- 平衡参数(如代码中c1=c2=1.2)有助于兼顾探索与开发。
4.代码与理论的对应关系
- 个体与群体经验:pBest和gBest分别对应文档中的“简单怀旧”和“群体规范”。
- 速度更新机制:代码中的w、c1、c2直接对应理论模型,省略了早期版本中的“疯狂”扰动。
- 边界处理:通过强制位置在[lb, ub]内模拟真实群体行为的空间约束。
- 自适应调整:通过bound动态约束搜索空间,确保解的可行性。
PSO通过简洁的群体智能模型实现高效优化,代码实现直观体现了理论核心。其成功依赖于参数调优与问题特性的匹配,未来可通过混合策略进一步提升性能
03.近年来相关论文发表
粒子群优化算法算法依旧活跃
04.本文代码效果图
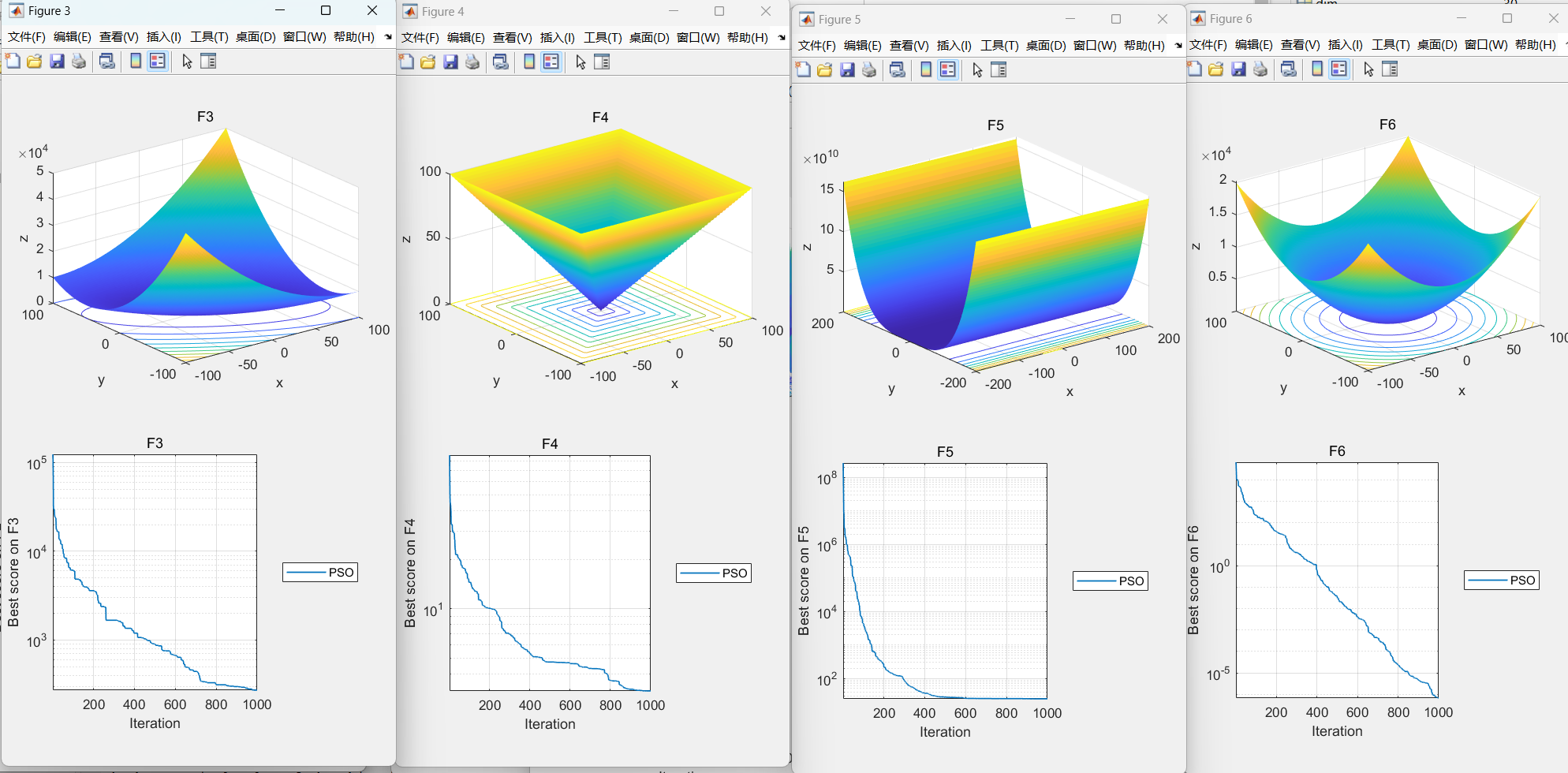
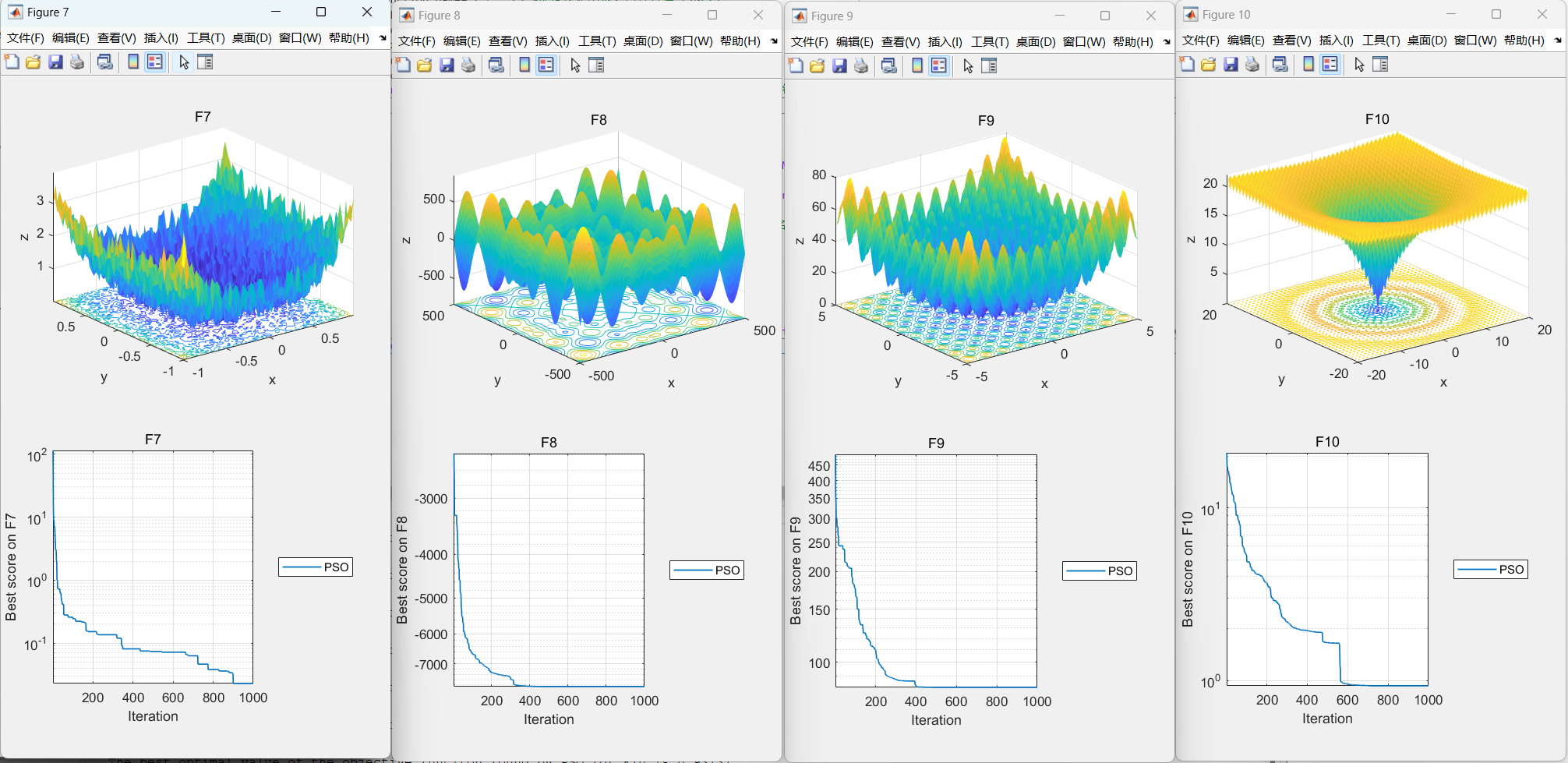
05.部分代码
% Particle Swarm Optimization
function [gBestScore,gBest,cg_curve]=PSO(N,iter,lb,ub,dim,y)
%PSO Infotmation
Vmax=ones(1,dim).*(ub-lb).*0.15; %速度最大值
noP=N;
w=0.85;
c1=1.2;
c2=1.2;
% Initializations
vel=zeros(noP,dim);
pBestScore=zeros(noP);
pBest=zeros(noP,dim);
gBest=zeros(1,dim);
cg_curve=zeros(1,iter);
% Random initialization for agents.
lb=ones(1,dim).*(lb); % Lower limit for variables
ub=ones(1,dim).*(ub); % Upper limit for variables
%% Initialization
for i=1:dim
pos(:,i) = lb(i)+rand(N,1).*(ub(i) - lb(i)); % Initial population
end
for i=1:noP
pBestScore(i)=inf;
end
% Initialize gBestScore for a minimization problem
gBestScore=inf;
for l=1:iter
% Return back the particles that go beyond the boundaries of the search space
for i=1:size(pos,1)
Flag4ub=pos(i,:)>ub;
Flag4lb=pos(i,:):)=(pos(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
end
for i=1:size(pos,1)
%Calculate objective function for each particle
fitness= y(pos(i,:) );
if(pBestScore(i)>fitness)
pBestScore(i)=fitness;
pBest(i,:)=pos(i,:);
end
if(gBestScore>fitness)
gBestScore=fitness;
gBest=pos(i,:);
end
end
%Update the W of PSO
%Update the Velocity and Position of particles
for i=1:size(pos,1)
for j=1:size(pos,2)
vel(i,j)=w*vel(i,j)+c1*rand()*(pBest(i,j)-pos(i,j))+c2*rand()*(gBest(j)-pos(i,j));
if(vel(i,j)>Vmax(j))
vel(i,j)=Vmax(j);
end
if(vel(i,j)<-Vmax(j))
vel(i,j)=-Vmax(j);
end
pos(i,j)=pos(i,j)+vel(i,j);
end
end
cg_curve(l)=gBestScore;
end
end
✅作者简介:信号处理方向在校博士研究生,目前专研于MATLAB算法及科学绘图等,熟知各种信号分解算法、神经网络时序、回归和分类预测算法、数据拟合算法以及滤波算法。提供一个可以相互学习相互进步的平台
🚩技术信仰:知行合一,让每一行代码都成为解决问题的利器
🔍后台添加博主微信并备注个人需求(比如 GA-BP)定制以下ALA算法优化模型:
1.回归/时序/分类预测类:BP、RF、XGBoost、RBF、LSSVM、SVM、ELM、DELM、ESN、RELM等等均可,优化算法优化BP为例,可达到以下效果:
2.分解类:EEMD、VMD、REMD、CEEMDAN、ICEEMDAN、SVMD等分解模型均可,优化算法优化VMD/ICEEMDAN为例,可达到以下效果:
(2)基于改进天鹰优化算法(IAO)优化ICEEMDAN参数
3.去噪算法算法类:VMD/CEEMDAN/ICEEMDAN/SVMD+小波阈值/SVD去噪,可在去噪算法前加智能优化算法优化参数以VMD-WT/SVD为例,可达到以下效果:
关注"MATLAB科研小白"后联系博主私家定制