算法思路介绍：

费舍尔线性判别分析（Fisher's Linear Discriminant Analysis，简称 LDA），用于将两个类别的数据点进行二分类。以下是代码的整体思路：

1. 生成数据：

• 使用 randn 函数生成随机数，构建两个类别的合成数据点。
• 第一个类别的数据点分布在以 (2,2) 为中心的正态分布中。
• 第二个类别的数据点分布在以 (-2,-2) 为中心的正态分布中。

1. 计算类别均值和散布矩阵：

• 计算每个类别的数据点的均值（类别中心）。
• 计算每个类别的散布矩阵（类别内离散度矩阵）。

1. 计算费舍尔线性判别：

• 计算费舍尔判别向量 W，它是使类间散布与类内散布的比值最大化的向量。
• 计算类内散布矩阵的总和 Sw。
• 利用线性代数中的求逆和乘法，计算出判别向量 W。

1. 生成测试样本 (x)：
2.    使用 randn 函数生成一个随机测试样本。
3. 对测试样本进行分类：
4.    将测试样本投影到判别向量 W 上，并与预先设定的阈值比较以进行分类。
5. 绘图：

• 绘制两个类别的数据点，以红色和蓝色表示。
• 标记测试样本点，并根据分类结果用不同的颜色表示。
• 绘制费舍尔判别线，表示分类的决策边界。
• 绘制判别线上的阈值点。
• 绘制测试样本在判别线上的投影点，并画出测试样本与其投影点之间的连线。

通过这些步骤，代码能够实现费舍尔线性判别分析，并对新的测试样本进行分类和可视化。

结果展示：

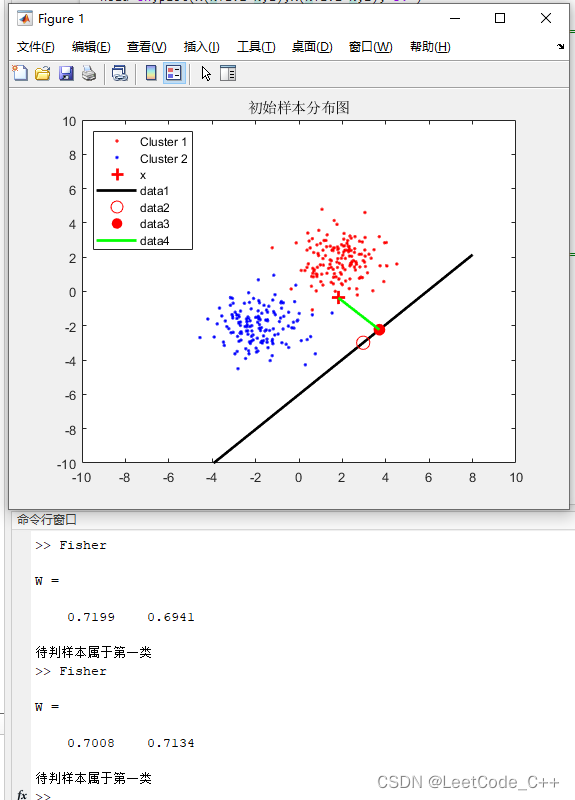
​​编辑​