代码介绍：https://zhuanlan.zhihu.com/p/700048609

压缩后，运行MyLSTM即可

介绍回顾：

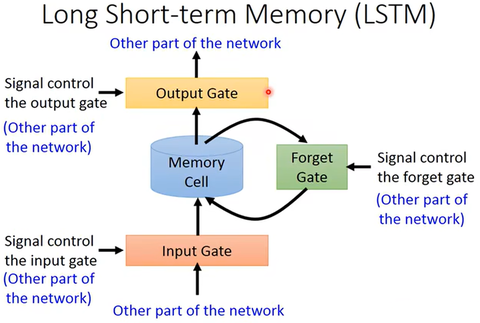
上一篇我们介绍了LSTM的理论框架

卷心菜：LSTM模型（1）：理论简介到混沌系统预测0 赞同 · 0 评论文章

不过原理是原理，不会用还是不行。这篇文章教你用Matlab实现一个LSTM来预测混沌系统的时间序列。

数据说明

我们这里用LSTM来拟合一个经典的混沌系统 - Lorenz系统。它由气象学家Edward Lorenz于1963年提出，这个系统由三个简单的非线性微分方程组成，但它们的行为却极其复杂，能够产生不可预测的混沌动态。它也是蝴蝶效应的经典例子。

首先，加载我们的数据是这个系统的 维坐标变化的时间序列，如下图所示

数据导入

% 导入数据
clear; clc; close all
data = load('Lorenz.mat').y(1,:)';
data = data';
figure(); 
plot(data, 'LineWidth',1)
grid on; box on;
xlim([1, length(data)])
xlabel('step'); ylabel('x')

接着，对我们的数据进行切分。将90%的数据用来训练，10%的数据用来测试。

train_num = floor(0.9*numel(data));
data_train = data(1:train_num+1);
data_test = data(train_num+1:end);

数据预处理

对训练数据进行归一化

mu = mean(data_train);
sig = std(data_train);
dataTrainStandardized = (data_train - mu) / sig; 
data_norm = (data - mu) / sig;

从数据中定义特征与标签

XTrain = dataTrainStandardized(1:end-1);
YTrain = dataTrainStandardized(2:end);

训练设置

接下来，是定义你所需要的网络结构了

layers = [
    sequenceInputLayer(1,"Name","input")    % 序列层，表示我们输入的是一维时间序列
    lstmLayer(64,"Name","lstm")             % 将上面的序列传递给LSTM层，这里我们用64个LSTM进行训练
    fullyConnectedLayer(1,"Name","fc")      % 输出层我们用一个全连接，而且输出的维数为1
    regressionLayer];                       % 这里可选标签是用来分类还是回归，因为是连续信号，所以选回归

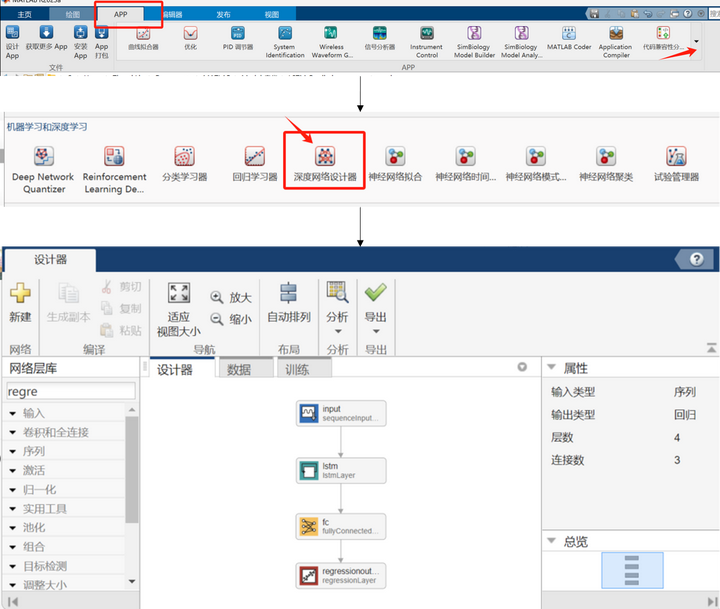
注：上面的网络结构可以在Matlab自带的网络设计器中打开和设计。设计路径如下

设计完成后，进行导出即可

定义训练参数并开始训练

options = trainingOptions('adam', ...       % 选择 Adam 优化器，可以避免过拟合
    'MaxEpochs',250, ...                    % 最大训练次数为 250 次
    'GradientThreshold',1, ...              % 梯度阈值，用于控制梯度的最大范数，超过该值会被裁剪
    'InitialLearnRate',0.005, ...           % 初始学习率为 0.005
    'LearnRateSchedule','piecewise', ...    % 使用分段学习率调度策略
    'LearnRateDropPeriod',125, ...          % 学习率下降周期为 125
    'LearnRateDropFactor',0.2, ...          % 学习率下降因子为 0.2
    'Verbose',0, ...                        % 关闭训练过程中的详细输出信息
    'Plots','training-progress');           % 显示训练进度图

net = trainNetwork(XTrain,YTrain,layers,options);   % 开始训练

此时会弹出一个预测进度框，可以实时看到训练的进度。

预测阶段

训练完成之后，我们训练好的模型存储在net变量中。我们用的预测方法是，先从 t 预测 t+1 的数据，然后将 t+1 的结果带回模型预测 t+2 的数据。

% 测试集数据处理
dataTestStandardized = (data_test - mu) / sig;
XTest = dataTestStandardized(1:end-1);
% 预测
net = predictAndUpdateState(net,XTrain);
[net,YPred] = predictAndUpdateState(net,YTrain(end));   % 先预测下一刻的数据

numTimeStepsTest = numel(XTest);
for i = 2:numTimeStepsTest
    % 不断迭代进行预测
    [net,YPred(:,i)] = predictAndUpdateState(net,YPred(:,i-1),'ExecutionEnvironment','cpu');
end

展示结果与画图

% 训练数据归一化
mu = mean(YTrain);
sig = std(YTrain);
dataTrainStandardized = (YTrain - mu) / sig; 

% 绘图
figure;
plot(dataTrainStandardized(1:end-1))
hold on
idx = train_num:(train_num+numTimeStepsTest);
plot(idx,[data_norm(train_num) YPred],'k.-'),hold on
plot(idx,data_norm(train_num:end-1),'r'),hold on
hold off
xlabel("Step")
ylabel("Value")
legend(["Observed" "Forecast"])

可以看到，在未来的100步时，预测的效果还算不错，但过了这个范围效果就变差了。毕竟每一步的预测都存在误差，而这种迭代的预测会造成误差的快速累加。以至于后期变得完全不一样了