蚱蜢优化算法(Grasshopper Optimization Algorithm,GOA)是期刊“IEEE Access”(IF 3.9)的2021年智能优化算法

01.引言
蚱蜢优化算法(Grasshopper optimization algorithm, GOA),并将其应用于结构优化中的挑战性问题。该算法在数学上模拟和模拟了自然界中蚱蜢群的行为,以解决优化问题。首先在包括CEC2005在内的一系列测试问题上对GOA算法进行基准测试,对其性能进行定性和定量的测试和验证。然后,利用该方法对52杆桁架、3杆桁架和悬臂梁进行了优化设计,验证了该方法的适用性。结果表明,与文献中已知的和最新的算法相比,所提出的算法能够提供更好的结果。实际应用的结果也证明了GOA在解决具有未知搜索空间的实际问题方面的优点。
02.优化算法的流程
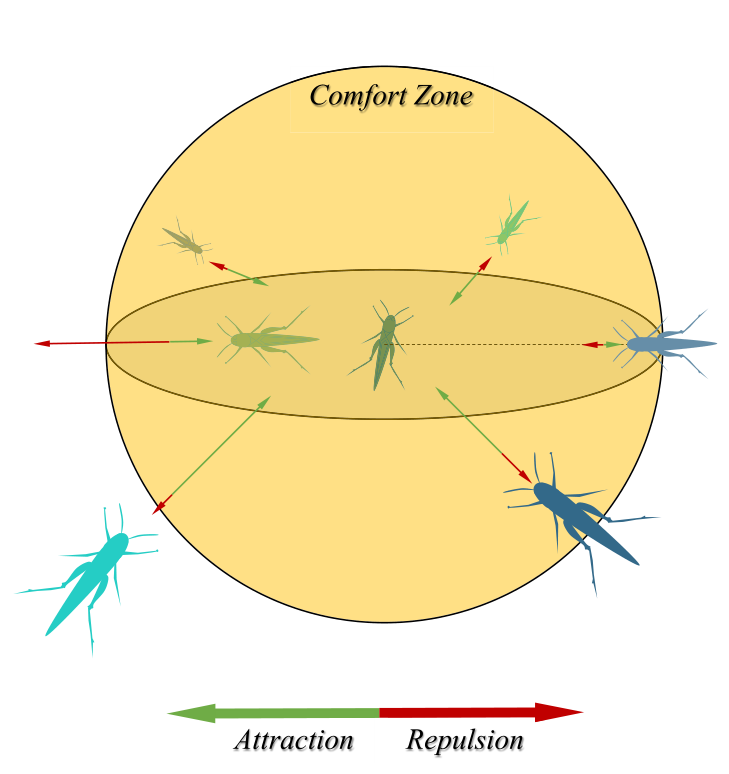

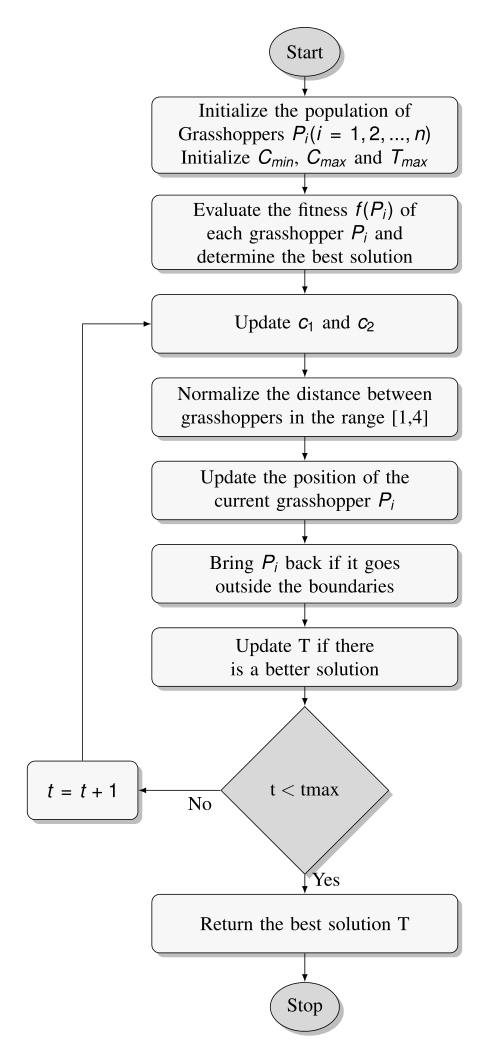
03.论文中算法对比图
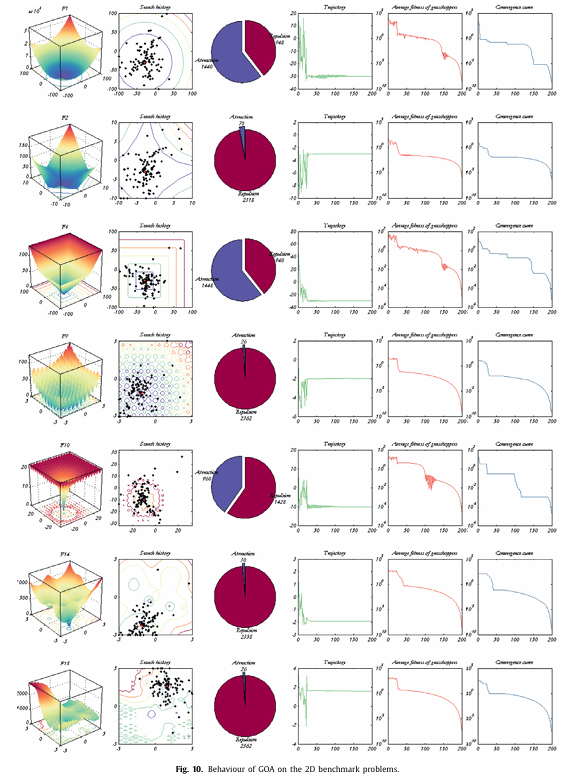

04.部分代码
% The Grasshopper Optimization Algorithm
function [TargetFitness,TargetPosition,Convergence_curve,Trajectories,fitness_history, position_history]=GOA(N, Max_iter, lb,ub, dim, fobj)
disp('GOA is now estimating the global optimum for your problem....')
flag=0;
if size(ub,1)==1
ub=ones(dim,1)*ub;
lb=ones(dim,1)*lb;
end
if (rem(dim,2)~=0) % this algorithm should be run with a even number of variables. This line is to handle odd number of variables
dim = dim+1;
ub = [ub; 100];
lb = [lb; -100];
flag=1;
end
%Initialize the population of grasshoppers
GrassHopperPositions=initialization(N,dim,ub,lb);
GrassHopperFitness = zeros(1,N);
fitness_history=zeros(N,Max_iter);
position_history=zeros(N,Max_iter,dim);
Convergence_curve=zeros(1,Max_iter);
Trajectories=zeros(N,Max_iter);
cMax=1;
cMin=0.00004;
%Calculate the fitness of initial grasshoppers
for i=1:size(GrassHopperPositions,1)
if flag == 1
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,1:end-1));
else
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,:));
end
fitness_history(i,1)=GrassHopperFitness(1,i);
position_history(i,1,:)=GrassHopperPositions(i,:);
Trajectories(:,1)=GrassHopperPositions(:,1);
end
[sorted_fitness,sorted_indexes]=sort(GrassHopperFitness);
% Find the best grasshopper (target) in the first population
for newindex=1:N
Sorted_grasshopper(newindex,:)=GrassHopperPositions(sorted_indexes(newindex),:);
end
TargetPosition=Sorted_grasshopper(1,:);
TargetFitness=sorted_fitness(1);
% Main loop
l=2; % Start from the second iteration since the first iteration was dedicated to calculating the fitness of antlions
while l1
c=cMax-l*((cMax-cMin)/Max_iter); % Eq. (2.8) in the paper
for i=1:size(GrassHopperPositions,1)
temp= GrassHopperPositions';
for k=1:2:dim
S_i=zeros(2,1);
for j=1:N
if i~=j
Dist=distance(temp(k:k+1,j), temp(k:k+1,i)); % Calculate the distance between two grasshoppers
r_ij_vec=(temp(k:k+1,j)-temp(k:k+1,i))/(Dist+eps); % xj-xi/dij in Eq. (2.7)
xj_xi=2+rem(Dist,2); % |xjd - xid| in Eq. (2.7)
s_ij=((ub(k:k+1) - lb(k:k+1))*c/2)*S_func(xj_xi).*r_ij_vec; % The first part inside the big bracket in Eq. (2.7)
S_i=S_i+s_ij;
end
end
S_i_total(k:k+1, :) = S_i;
end
X_new = c * S_i_total'+ (TargetPosition); % Eq. (2.7) in the paper
GrassHopperPositions_temp(i,:)=X_new';
end
% GrassHopperPositions
GrassHopperPositions=GrassHopperPositions_temp;
for i=1:size(GrassHopperPositions,1)
% Relocate grasshoppers that go outside the search space
Tp=GrassHopperPositions(i,:)>ub';Tm=GrassHopperPositions(i,:)';GrassHopperPositions(i,:)=(GrassHopperPositions(i,:).*(~(Tp+Tm)))+ub'.*Tp+lb'.*Tm;
% Calculating the objective values for all grasshoppers
if flag == 1
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,1:end-1));
else
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,:));
end
fitness_history(i,l)=GrassHopperFitness(1,i);
position_history(i,l,:)=GrassHopperPositions(i,:);
Trajectories(:,l)=GrassHopperPositions(:,1);
% Update the target
if GrassHopperFitness(1,i)In iteration #', num2str(l), ' , target''s objective = ', num2str(TargetFitness)])
l = l + 1;
end
if (flag==1)
TargetPosition = TargetPosition(1:dim-1);
end
end
function d = distance(a,b)
d=sqrt((a(1)-b(1))^2+(a(2)-b(2))^2);
end
function o=S_func(r)
f=0.5;
l=1.5;
o=f*exp(-r/l)-exp(-r); % Eq. (2.3) in the paper
end
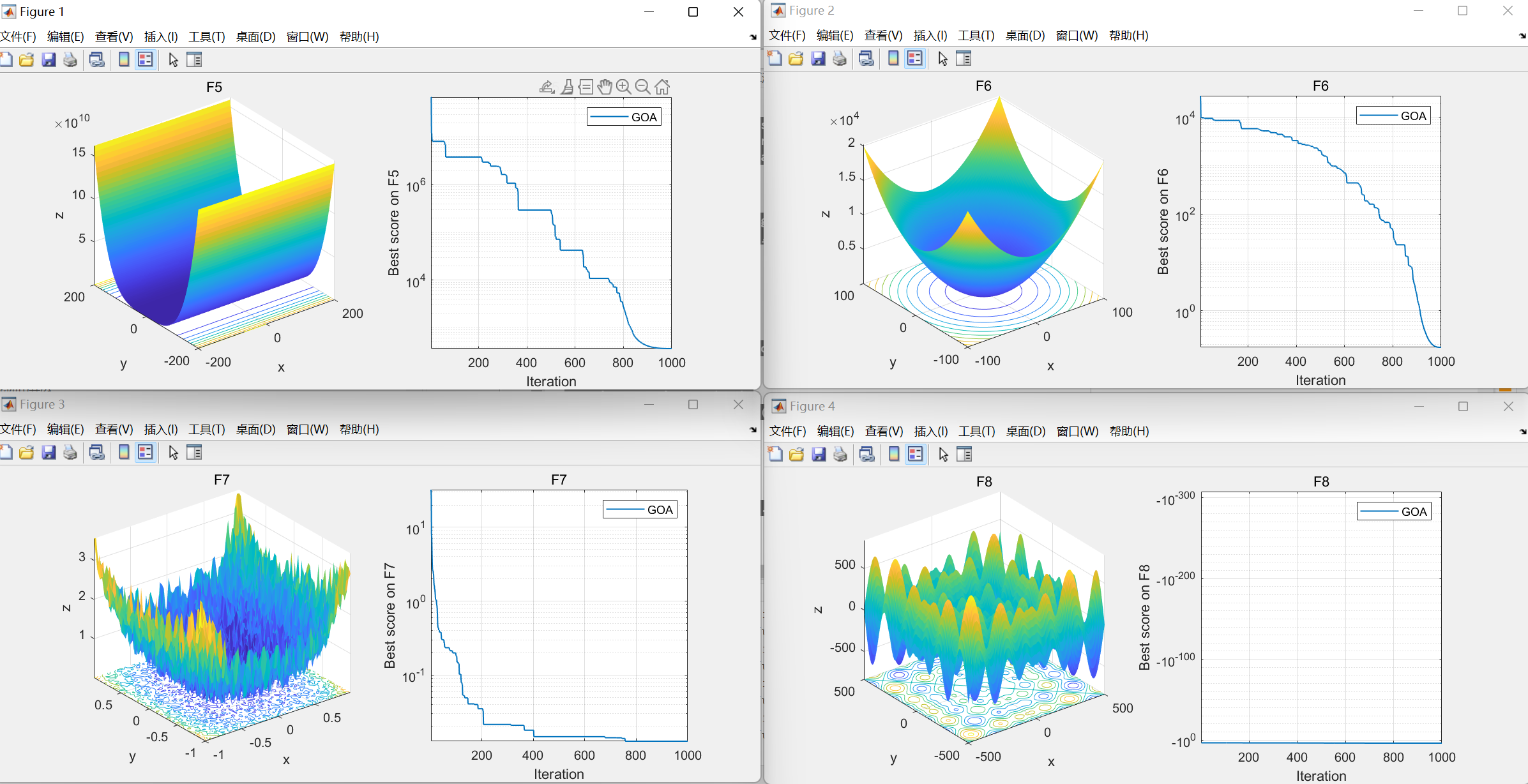
04.本代码效果图