1主要内容

该程序复现文章《A Fully Adaptive DRO Multistage Framework Based on MDR for Generation Scheduling under Uncertainty》，程序实现了一种基于混合决策规则（MDR）的完全自适应分布鲁棒多阶段框架，用于风电不确定性条件下的调度，以适应快速启动机组状态决策和调度过程中考虑非预期性的风力发电。与现有的多阶段模型相比，该框架引入了改进的MDR来处理所有的决策变量，以扩展可行区域。因此，该模型可以为解决传统模型中不可行的一些问题找到可行的解决方案，同时为可行的问题找到更好的解决方案，从而更好地利用风能，从而降低化石燃料的消耗。此外，采用先进的优化方法对该模型进行了重新表述，并将MDR改进为混合整数线性规划（MILP），以解决计算困难的问题。通过对IEEE案例研究，验证了该模型的有效性和优越性。程序采用matlab+cplex/mosek进行求解，注释清晰，方便学习！

• 不确定性设置

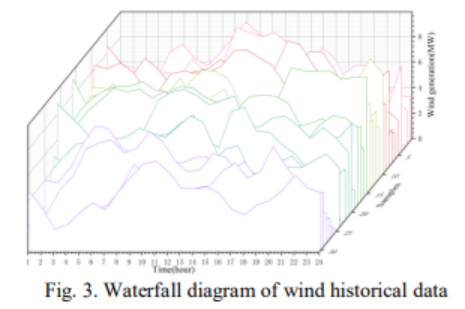
文章中不确定性采用如下设置方式，首先通过风电历史数据建立了风电运行集合，然后计算风电出力均值，从而计算得到风电出力历史值与均值差值，最后，构造出风电出力波动量的范围。通过与代码进行对比，能够看出，模型和程序的对应性很好，非常方便学习。 

该部分程序代码如下：

% 计算 uncertainty set
PW = []; % 将风力发电整合到一个大矩阵中，每列按先变t后i排列
for i = 1:W
    PW = [PW; Wind_data{1,i}];
end
PW = [PW(1:T,:);PW(24+1:24+T,:)];
% for i = 1:W
%     PW = [PW; 0.05*ones(24,30)];
% end
% 风力发电均值
PW_miu = zeros(W*T,1);
for i = 1:M
    PW_miu = PW_miu + PW(:,i);
end
PW_miu = PW_miu / M;
% 风电偏差
VW = zeros(W*T,M);
for j = 1:M
    VW(:,j) =  PW(:,j) - PW_miu;
end
VW_positive =  max(VW,[],2);
VW_negative =  min(VW,[],2);
% ksi 支撑集
ksi_positive = [1;VW_positive];
ksi_negative = [1;VW_negative];
% end of 计算 uncertainty set

2部分代码

% 连续变量定义 每个时段变量数不同，在用到时定义
YG = sdpvar(G,T+W*bN*leng_k); %火力机组出力决策变量，系数矩阵按Y0,分段，风电机组，时段排列
% YG = 1:64;
% YG = [YG;YG;YG;YG;YG;YG];
Ytheta = sdpvar(N,T+W*bN*leng_k); %节点相角决策变量，每个节点都有theta，不止发电机节点有，所以有N行
Yz = sdpvar(G,T+W*bN*leng_k); % 火力机组出力费用决策变量
YS = sdpvar(G,T+W*bN*leng_k); % 火力机组开机费用决策变量
YPw = sdpvar(W,T+W*bN*leng_k); %W行，W个风电机组
Yl = sdpvar(N,T+W*bN*leng_k); %切负载决策变量
% 整型变量
% 是取值为-1，0，1的整型变量，不是0，1binary变量
Xu = intvar(G,T+W*bpN*leng_k); %机组状态决策变量
Xs = intvar(G,T+W*bpN*leng_k); %开机动作决策变量
Xd = intvar(G,T+W*bpN*leng_k); %关机动作决策变量
​
% 开始约束构造
cons = [];
cons = [cons, -1 <= Xu <= 1]; % 将整型决策变量约束在-1，0，1
cons = [cons, -1 <= Xs <= 1];
cons = [cons, -1 <= Xd <= 1];
​
% 参考节点
%每个模型都只设定第一个节点为参考节点？
Ytheta(1,:) = zeros(1,T+W*bN*leng_k); %每个节点都有theta，不止发电机节点有，所有有N行
% end of 参考节点
​
% 初始状态保持
for g = 1:G % 设置了开始都是关机，所以这里保持关机状态。没考虑初始是开机情况
    for t = 1:(U0(g)+L0(g))
        Xu(g,T+1+Sumt(t-1)*W*bpN:T+Sumt(t)*W*bpN) = zeros(1,t*W*bpN); %将需要保持关机态时段Xu的决策变量系数置零
        Xu(g,t) = 0; %Xu0 也要置零
    end
end
% end of 初始状态保持
​
% 不等式约束统一构造
% 构造通用的U矩阵，h向量 公用常量
Uc_l = []; %迭代生成顶点矩阵
Uc_c = []; %lamda系数矩阵
Uc = [];
Uconstant_0 = []; %顶点系数lamda组合为1约束的系数矩阵 for ksi0
Uconstant_0 = blkdiag(1, Uconstant_0);%在最开始为Uconstant矩阵补上系数1 for ksi0 常数项
Uconstant_0 = blkdiag(1, Uconstant_0);%在最开始为Uconstant矩阵补上系数1 for ksi_hat0 常数项
Uconstant_0 = blkdiag(1, Uconstant_0);%在最开始为Uconstant矩阵补上系数1 for ksi_tine0 常数项
Ulamda_0 = [];
Ulamda_0 = blkdiag(-1, Ulamda_0); %在最开始为Ulamda矩阵补上系数-1 for ksi0 常数项
Ulamda_0 = blkdiag(-1, Ulamda_0); %在最开始为Ulamda矩阵补上系数-1 for ksi_hat0 常数项
Ulamda_0 = blkdiag(-1, Ulamda_0); %在最开始为Ulamda矩阵补上系数-1 for ksi_tine0 常数项
for t = 1:T
    Uconstant = []; %顶点系数lamda组合为1约束的系数矩阵
    for w = 1:W
        Uconstant = blkdiag(Uconstant,ones(1,vN));
    end
    Ulamda = blkdiag(-verts(:,1+(t-1)*2*vN:vN+(t-1)*2*vN),-verts(:,1+vN+(t-1)*2*vN:2*vN*t)); %顶点凸组合表示ksi约束的系数矩阵
    Uc_l = blkdiag(Ulamda_0,Uc_l); % U矩阵上部分，由凸包顶点构成
    Uc_l = blkdiag(Uc_l,Ulamda); % U矩阵上部分，由凸包顶点构成
    Uc_c = blkdiag(Uconstant_0,Uc_c); %U矩阵下部分，由1组成实现顶点系数求和为1
    Uc_c = blkdiag(Uc_c,Uconstant); %U矩阵下部分，由1组成实现顶点系数求和为1
    Uc = [Uc_l;Uc_c]; %凸包等式约束U矩阵
    Wc_l = diag(ones(t*W*kl+3*t,1)); %W矩阵上部分，单位阵
    Wc_c = zeros(t*W+3*t,t*W*kl+3*t); %W矩阵下部分，0矩阵
    Wc = [Wc_l;Wc_c];
    hc = [zeros(t*W*kl + 3*t,1);ones(t*W+3*t,1)]; %构造常数项向量 = 两倍的Z向量长度
    for n = 1:N %遍历所有节点
        % 功率切割上界约束
        Lamda_lup = [sdpvar(t*W*kl + 3*t,1); sdpvar(t*W + 3*t,1)]; %构造等式对偶乘子lamda向量 = h向量维度
        Lamda2_lup = sdpvar((t*W)*vN + 3*t,1); %构造不等式对偶乘子lamda向量 = verts维度
        Zlup = -Zhat(Yl,t,T,W,n,Lup(n,1),bpN,bN);
        cons = [cons, Wc'* Lamda_lup == Zlup'];
        cons = [cons, Uc'* Lamda_lup + Lamda2_lup == 0];
        cons = [cons, hc'* Lamda_lup >= 0];
        cons = [cons, Lamda2_lup >= 0];
        % 功率切割下界约束

3部分程序结果

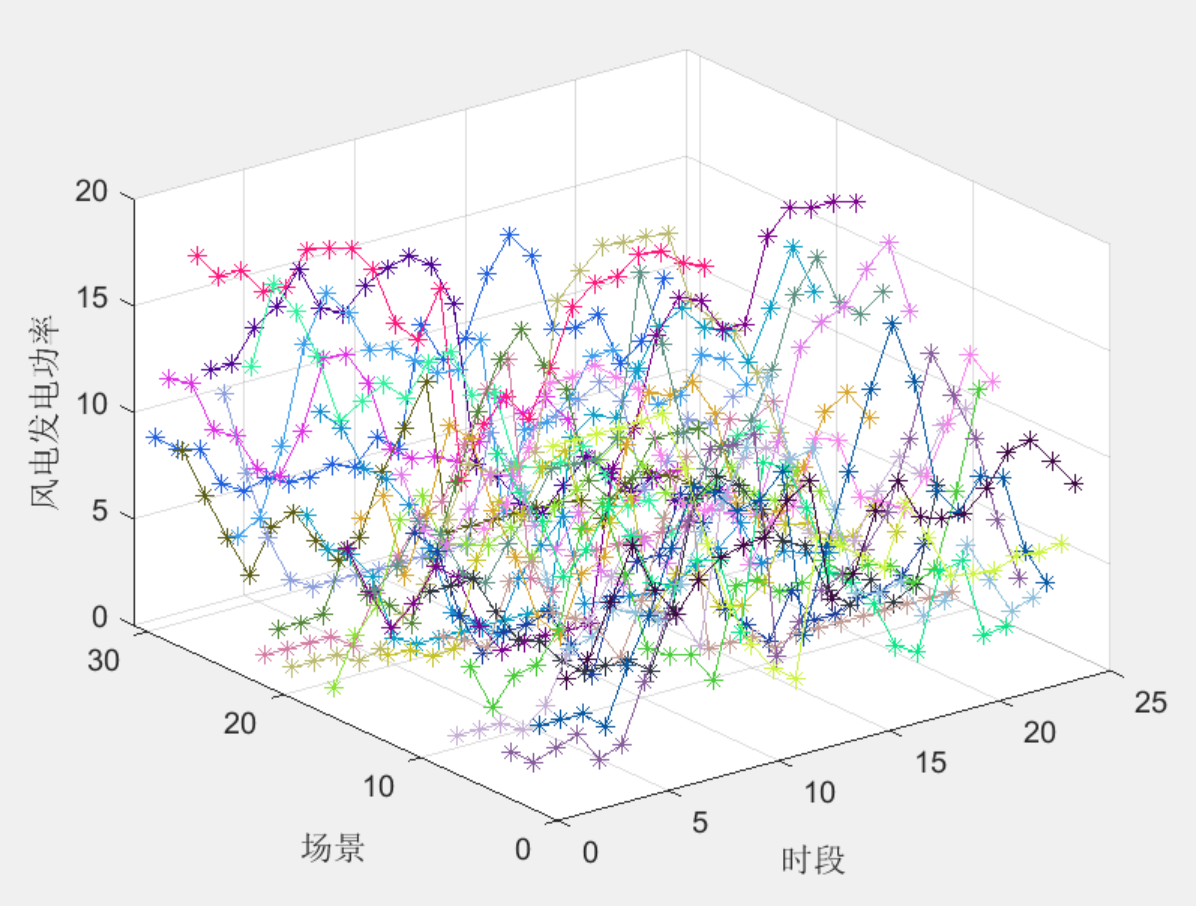
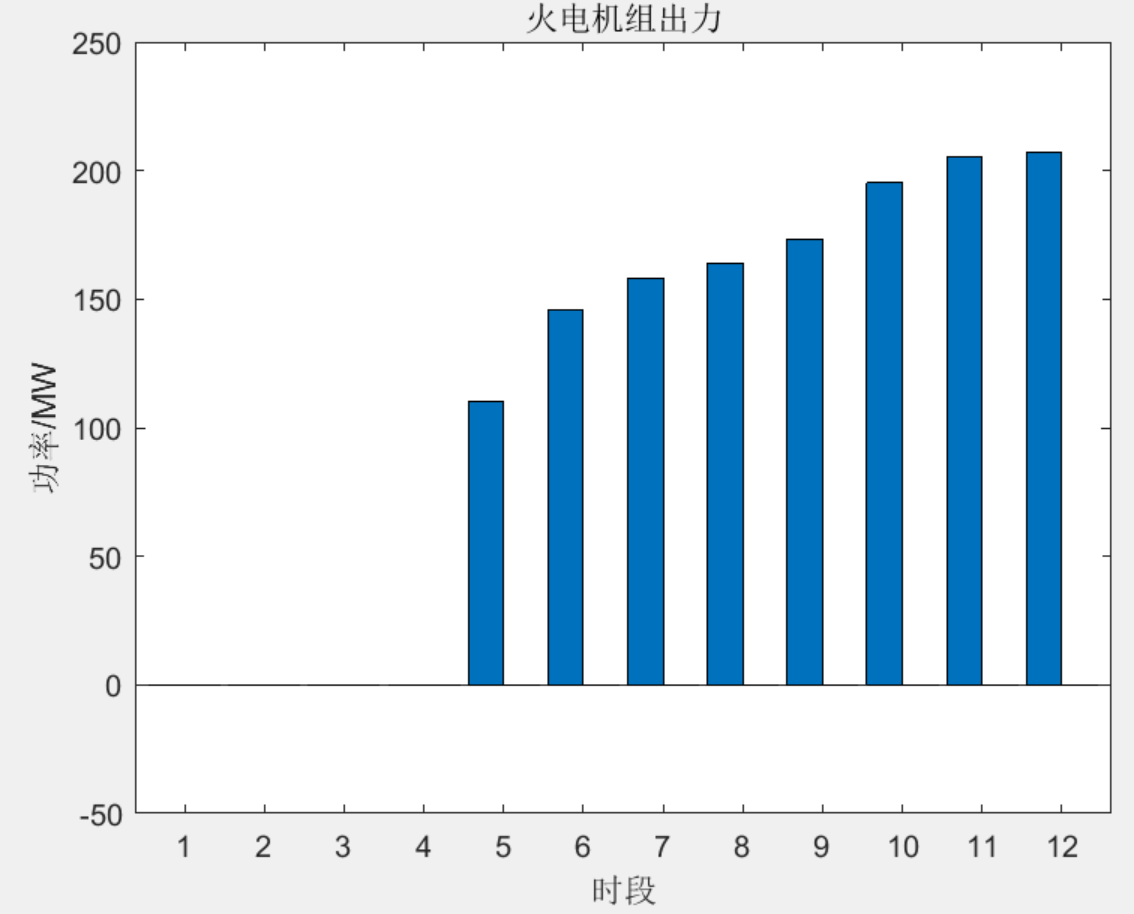
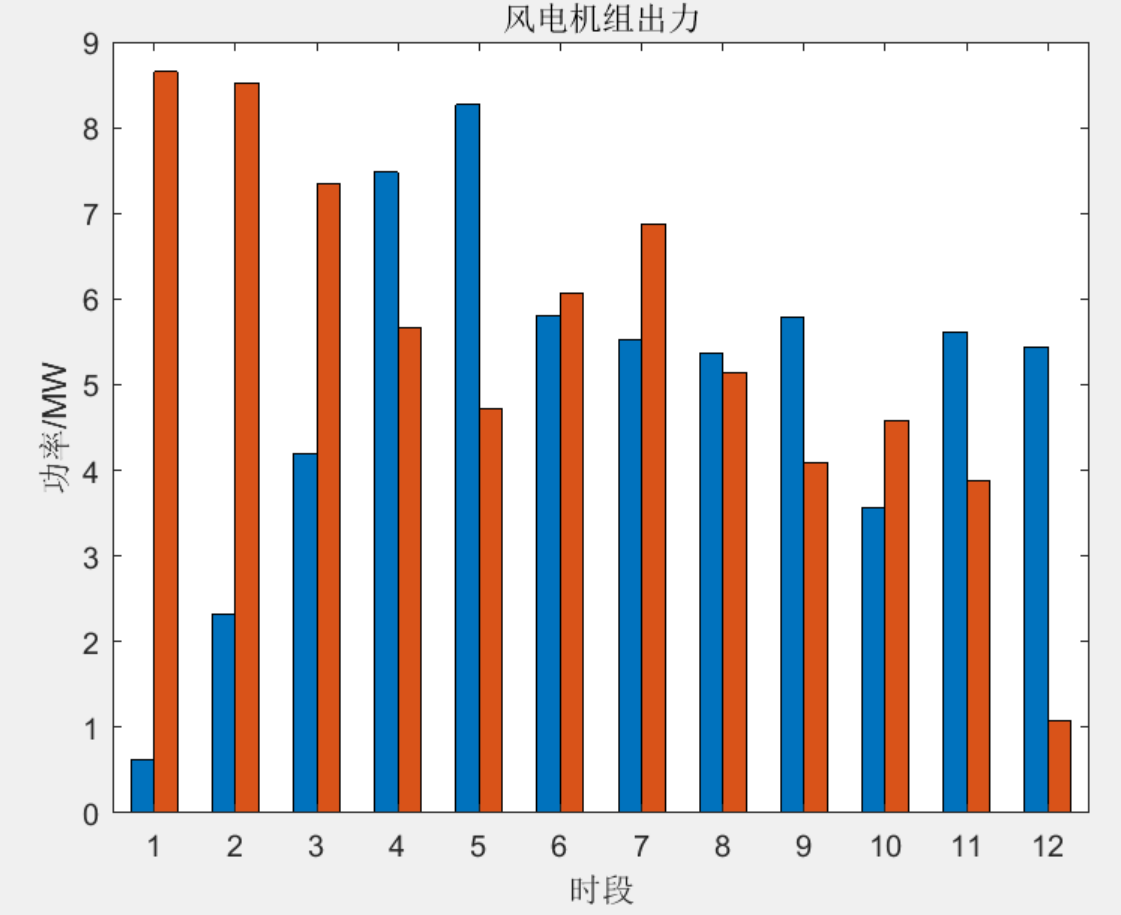
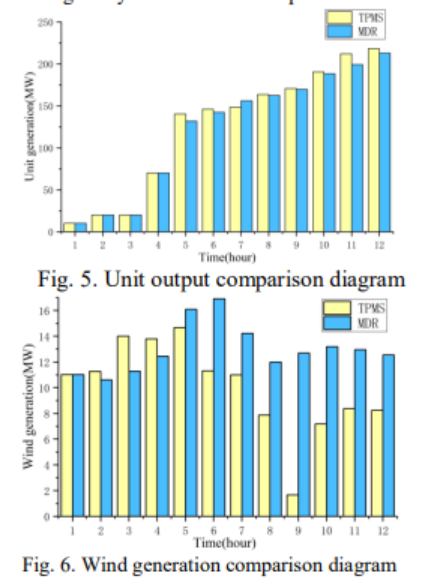
原文结果如下：