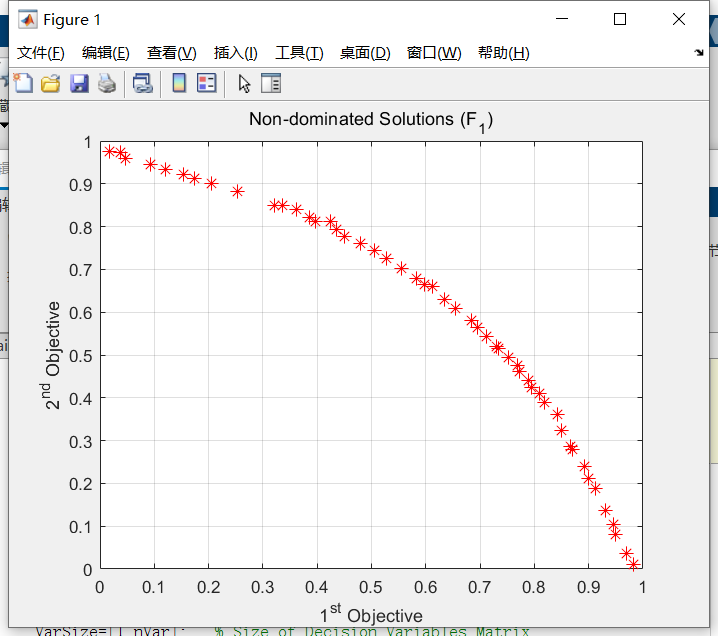
非支配性排序多目标遗传算法II(Non-dominated Sorting Genetic Algorithm II,简称NSGA-II)是一种用于解决多目标优化问题的经典算法。NSGA-II是基于遗传算法的一种演化算法,它通过模拟自然选择和遗传进化的过程,搜索出 Pareto 最优解集合,以提供多个非支配解的选择。
NSGA-II的实现原理如下:
- 初始化种群: 随机生成初始种群,其中每个个体都是一个可能的解决方案。
- 评估适应度: 对初始种群中的个体进行适应度评估,这意味着对每个个体应用目标函数,以确定它们在目标空间中的性能。
- 非支配性排序: 对种群中的个体进行非支配性排序。首先,计算每个个体的被其他个体所支配的个数(即支配该个体的个体数量),并将其分类为不同的 Pareto 前沿中的层级。这些层级中的个体不被任何其他个体所支配,因此它们构成 Pareto 最优解的第一层。然后,将这些个体从种群中移除,并重复该过程以找到下一层 Pareto 最优解,直到所有个体都被分类为 Pareto 前沿。
- 计算拥挤度: 在每个 Pareto 前沿中,对个体按照其在目标空间中的密度进行排序。这可以通过计算个体之间的距离来实现。通常使用欧氏距离或其他距离度量来衡量个体之间的相对位置。
- 选择操作: 通过结合非支配性排序和拥挤度计算,从当前种群中选择优良的个体作为下一代种群的父代。具体来说,NSGA-II倾向于选择 Pareto 前沿中较低层级的个体,同时在同一层级中选择拥挤度较低的个体,以保持多样性和收敛性。
- 交叉和变异: 对选定的父代进行交叉和变异操作,生成新的个体。这些操作有助于增加种群的多样性,并在每一代中引入新的解决方案。
- 替换操作: 将新生成的个体与当前种群进行替换,以形成下一代种群。
- 重复进化过程: 重复以上步骤,直到达到预定义的停止条件,例如达到最大迭代次数或找到满意的 Pareto 最优解。