本作品包括数据集、代码、模型、项目介绍等内容,并对传统的wknn算法进行了改进!!!!
实验环境
实验环境是使用Python编程语言,在Python环境中运行。此外,该程序还使用了多个Python第三方库,包括:
1. Pandas:用于数据读取和处理。
2. NumPy:用于数据处理和数学计算。
3. sklearn:用于机器学习模型的训练和评估。
4. Matplotlib:用于数据可视化。
在程序中使用了KNN和WKNN回归算法,分别用于预测三维空间中的位置坐标。程序使用了CSV格式的数据集文件,并使用Pandas库读取和处理数据。程序还使用了joblib库来保存训练好的模型。
程序介绍
1、导入必要的库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import joblib
这里导入了需要用到的库,包括pandas用于数据处理,numpy用于数组处理,sklearn中的KNeighborsRegressor用于KNN回归模型的构建,matplotlib用于数据可视化,joblib用于模型保存。
2、加载数据集
data = pd.read_csv('dataset1.csv', sep=';')
这里使用pandas库中的read_csv()函数读取csv文件,并将分隔符设置为';'。读取后的数据保存在data变量中。
3、处理特征向量
X = data.iloc[:, 13:44].replace('null', np.nan).astype(float).fillna(0).values
这里选取了data中的第13列到第43列的数据作为特征向量,用于训练模型。由于有些数据缺失,使用replace()函数将其替换为np.nan,然后使用astype()函数将数据类型转换为float,最后使用fillna()函数将缺失值替换为0
4、获取标签x、y、z
y_xyz = data.iloc[:, 2:5].astype(float).values
这里选取了data中的第2列到第4列的数据作为标签,即三维坐标的x、y、z值。同样使用astype()函数将数据类型转换为float。
5、将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y_xyz, test_size=0.2, random_state=42)
这里使用sklearn库中的train_test_split()函数将数据集分为训练集和测试集。其中,X和y_xyz分别作为特征向量和标签,test_size表示测试集的大小比例,random_state表示随机种子,保证每次运行的结果一致。
6、创建KNN回归器
knn = KNeighborsRegressor(n_neighbors=5)
这里创建了一个KNN回归器,并将n_neighbors参数设置为5,表示使用最近的5个邻居来进行预测。
7、在训练集上训练回归器
knn.fit(X_train, y_train)
这里使用fit()函数在训练集上训练KNN回归器。
8、在测试集上评估回归器性能
y_pred = knn.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_test, y_pred)
print("KNN均方误差 Root Mean Squared Error: ", rmse)
print("KNN平均绝对误差 Mean Absolute Error: ", mae)
这里使用predict()函数在测试集上进行预测,并使用mean_squared_error()和mean_absolute_error()函数计算预测结果与真实结果之间的均方误差和平均绝对误差,输出评估结果。
9、定义不同权重函数
def inverse_distance(distances):
return 1 / distances
def inverse_distance_squared(distances,epsilon=1e-8):
distances = np.maximum(distances, epsilon)
return 1 / distances**2
def distance_weight(distances):
return 1 / (1 + distances)
这里定义了三个不同的权重函数,用于WKNN回归器的构建。其中,inverse_distance()函数返回距离的倒数作为权重,inverse_distance_squared()函数返回距离的倒数平方作为权重,distance_weight()函数返回距离的倒数加1的倒数作为权重。
我们首先使用inverse_distance()、inverse_distance_squared()和distance_weight()函数创建了三个不同的WKNN回归器,并分别命名为wknn_id、wknn_ids和wknn_dw。然后,我们在训练集上对这三个回归器进行了训练。
接着,我们使用predict()函数在测试集上进行预测,并使用mean_squared_error()和mean_absolute_error()函数分别计算了预测结果和真实结果之间的均方误差和平均绝对误差,并将评估结果输出到控制台中。最后,我们可以根据输出结果进行模型选择和调整。
可视化展示
三维空间分布图,用于展示预测结果和真实结果在三维空间中的分布情况,其中蓝色的点表示真实结果,红色的点表示预测结果。这个图形化展示可以帮助我们直观地了解预测结果和真实结果的分布情况,以及模型是否能够准确地预测三维空间中的结果
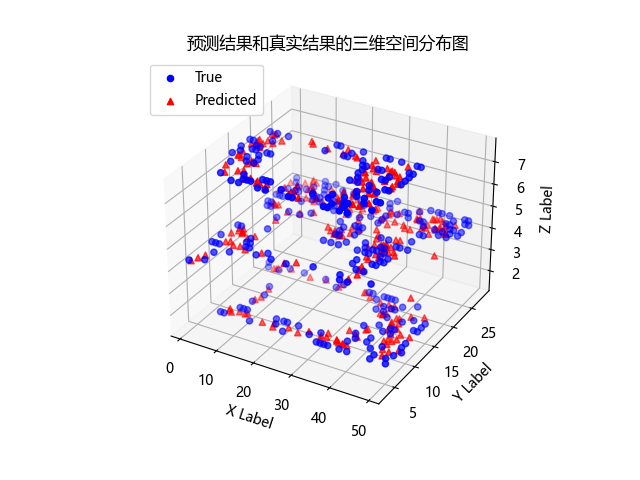
散点图,用于展示预测结果和真实结果在二维平面上的分布情况,其中蓝色的点表示真实结果,红色的点表示预测结果。这个图形化展示可以帮助我们直观地了解预测结果和真实结果在二维平面上的分布情况,以及模型是否能够准确地预测二维平面上的结果。
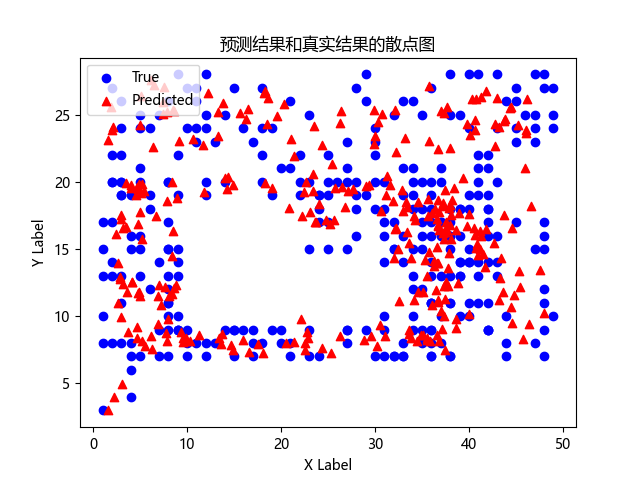
误差分布图,用于展示预测结果和真实结果之间的误差分布情况。这个图形化展示可以帮助我们直观地了解模型的误差分布情况,以及模型是否能够准确地预测结果。
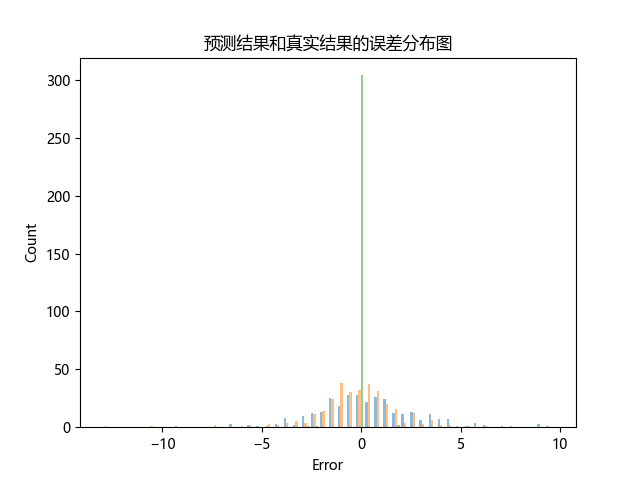
动态可视化,用于展示预测结果和真实结果在三维空间中的实时动态分布情况。这个图形化展示可以帮助我们更好地理解模型的性能和预测结果的准确性,以及模型在预测过程中的实时表现。
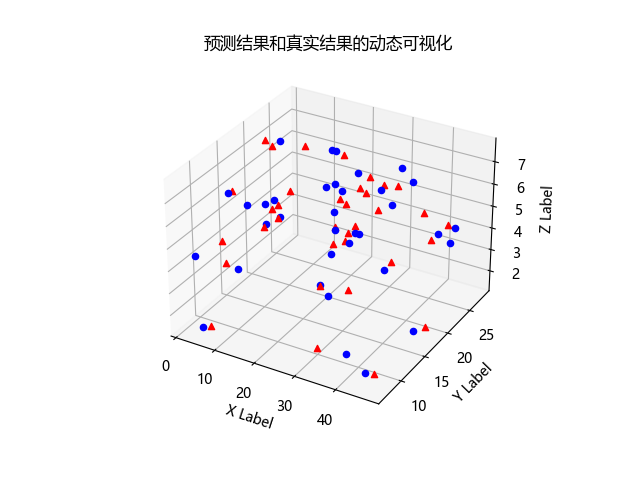
knn和wknn两者精确度对比
KNN均方误差 Root Mean Squared Error: 1.9911102213137062
KNN平均绝对误差 Mean Absolute Error: 1.1835281385281382
WKNN权重为inverse_distance均方误差 Root Mean Squared Error: 1.9736306217976498
WKNN权重为inverse_distance平均绝对误差 Mean Absolute Error: 1.1677008251607548
WKNN权重为inverse_distance_squared均方误差 Root Mean Squared Error: 1.9641521326399896
WKNN权重为inverse_distance_squared平均绝对误差 Mean Absolute Error: 1.1536246973899613
WKNN权重为distance_weight均方误差 Root Mean Squared Error: 1.9742903443363213
WKNN权重为distance_weight平均绝对误差 Mean Absolute Error: 1.1685954537506553
结论
wknn比knn更加精确!!!!!