当大家面临着复杂的数学建模问题时，你是否曾经感到茫然无措？作为2021年美国大学生数学建模比赛的O奖得主，我为大家提供了一套优秀的解题思路，让你轻松应对各种难题。

我的解题思路是基于数学建模领域的前沿理论和实践研究，具有极强的创新性和实用性。我深入分析了各种数学建模问题，并总结出了一套行之有效的解决方案，帮助大家在竞赛中脱颖而出，或在实际情景中解决问题。我们的团队既注重理论分析，又重视实际应用。在此次美赛中，我们依据实际问题出发，结合数学建模理论进行分析，并给出可行的解决方案。通过我的解题思路，你可以快速理解各种数学建模问题，并有效地解决它们。

我的解题思路的实用性得到了众多用户的认可，许多人已经使用我的方法成功地解决了各种问题，了解了各种思路和技巧。通过使用我的解题思路，大家可以快速理解和掌握数学建模问题，并且取得更好的成绩和效果。

希望这些想法对大家的做题有一定的启发和借鉴意义。

问题重述：

A题: 电采暖负荷参与电力系统功率调节的技术经济分析。

典型住户电采暖负荷用电行为分析： a) 分析典型房间温变过程微分方程稳态解的性态，包括制热功率、室内温度和墙体温度的变化特点，并分析模型参数对稳态解变化规律的影响。 b) 在给定室外温度的情况下，计算并绘制一日24小时的室内温度变化和电采暖设备开关状态曲线，并统计相关特征量。

典型住户电采暖负荷参与功率调节的能力分析： a) 以单个住户电采暖负荷为对象，计算在室外温度为-15℃、室内初始温度为20℃，电采暖设备开关初始状态为开启的情况下，每日24小时内功率上调和下调的可持续时间，并绘制计算结果。 b) 对于给定的不同室外温度，计算电采暖负荷功率上调和下调的可持续时间，并分析室外温度对功率调节特性的影响。

多个电采暖负荷的调节能力分析： a) 以6个电采暖住户为例，计算室外温度为-20℃、室内初始温度在温控区间内均匀分布的情况下，每日24小时内各时点电采暖设备的开关状态和总用电功率曲线。 b) 基于总用电功率曲线，计算每日24小时内各时点的电采暖负荷可参与上调和下调的总功率，并绘制计算结果。 c) 在给定的不同室外温度下，重新分析上述情况，并分析室外温度对电采暖设备可调节能力的影响。

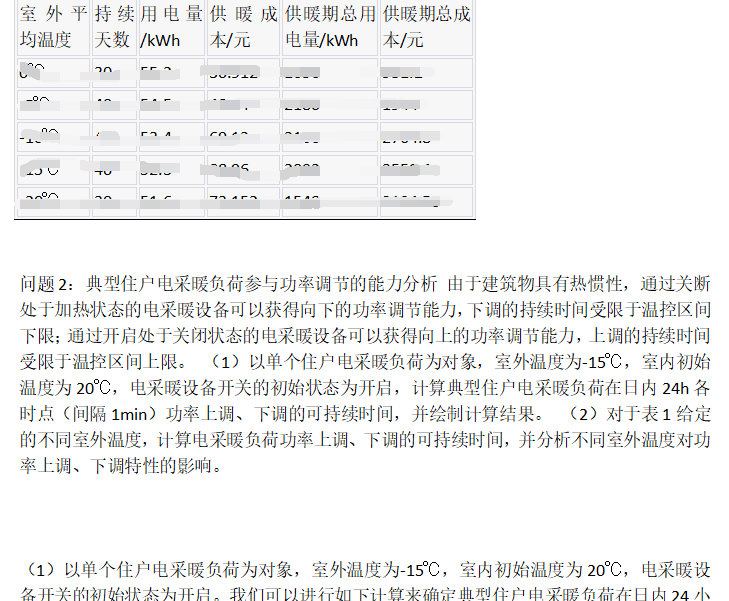
住宅区电采暖负荷参与电网调节的能力分析： a) 以600个住户为分析对象，计算在给定各室外平均温度下，每日24小时内住宅区电采暖设备的开关状态和总用电功率曲线。 b) 基于总用电功率曲线，计算每日24小时内住宅区电采暖负荷可参与上调和下调的总功率曲线。

住宅区电采暖负荷参与电网削峰填谷的收益分析： a) 计算600户电采暖负荷在削峰时段可持续提供的最大向下调节功率值。 b) 计算600户电采暖负荷在填谷时段可持续提供的最大向上调节功率值。 c) 统计各时点由于参与电网调节导致开关状态发生变化的电采暖设备数量，并绘制所有住户的室内温度曲线，检验参与调节后温度变化是否满足温控区间约束。 d) 估算在供暖期为180天，室外平均温度及持续天数已给出的情况下，住宅区电采暖负荷参与削峰填谷的上调和下调功率，并根据辅助服务补偿价格计算全年该住宅区电采暖负荷参与削峰填谷的总收益、平均每户收益以及节省的供热成本百分比。

温控型负荷参与电网调节展望： a) 分析基于600户电采暖负荷参与电网调节的计算结果，展望面积为4000万平方米的省级区域电采暖负荷参与电网调节的潜能，并讨论可能遇到的问题，并提出建议和解决方案。 b) 分析南方省份的温控型负荷主要是空调的特点，探讨展望空调负荷参与电网调节的潜能，并讨论可能遇到的问题。

 为了刻画电采暖负荷参与电网调节的功率/电量特性，并进行经济收益评价，我们可以按照以下步骤进行分析和计算。

典型住户电采暖负荷用电行为分析

(1) 在满足温控区间约束条件下，分析典型房间温变过程微分方程稳态解的性态，包括制热功率Pheat(t)、室内温度qin(t)和墙体温度qwall(t)的变化特点，并分析模型参数对稳态解变化规律的影响。

根据附件A中给出的典型住户模型参数，可以使用常微分方程模拟室内温度的变化过程。根据稳态解的性态，可以计算出制热功率Pheat(t)、室内温度qin(t)和墙体温度qwall(t)的变化特点。

为了分析典型房间温变过程的微分方程稳态解，我们可以利用能量守恒定律和热传导定律建立方程。

首先，我们可以建立室内空气的能量守恒方程：

其中，C_in是 室内空气的等效热容，qin(t)是室内温度，qwall(t)是墙体温度，P_heat(t)是电采暖设备的制热功率，R_1是室内空气和墙体内侧的等效热阻。

接下来，我们可以建立墙体的能量守恒方程：

其中，C_wall是墙体的等效热容，q_out(t)是室外温度，R_2是墙体外侧和室外空气的等效热阻。

一些内容show~