1 基本定义

添加积分约束的多项式拟合算法是一种基于多项式拟合的方法，它通过添加积分约束，得到一条更加平滑的拟合曲线，以达到更好的拟合效果。该算法的主要思想是通过在多项式系数中添加积分项，使得拟合曲线在一定程度上满足平滑性的约束条件。 具体来说，添加积分约束的多项式拟合算法的步骤如下：

1. 给定一组数据点{(x1, y1), (x2, y2), ..., (xn, yn)}。
2. 假设拟合曲线为y = f(x)，其中f(x)为一个n次多项式。
3. 在多项式系数中添加积分项，得到一个新的目标函数： ∑(yi-f(xi))^2 + λ∫(f''(x))^2dx 其中，f''(x)为拟合曲线的二阶导数，λ为平滑参数，用于调节拟合曲线的平滑程度。
4. 求解 n+1 个未知系数 a0, a1, ..., an，使得目标函数最小。添加积分约束的多项式拟合算法的优点是可以在一定程度上满足平滑性的约束条件，保留数据的整体趋势，同时对于一些具有明显曲率的数据也有较好的拟合效果。缺点是需要选择合适的平滑参数，以达到最优的拟合效果。此外，该算法对于一些存在极端值的数据也可能会对拟合结果产生较大的影响。

2 定义和出图效果

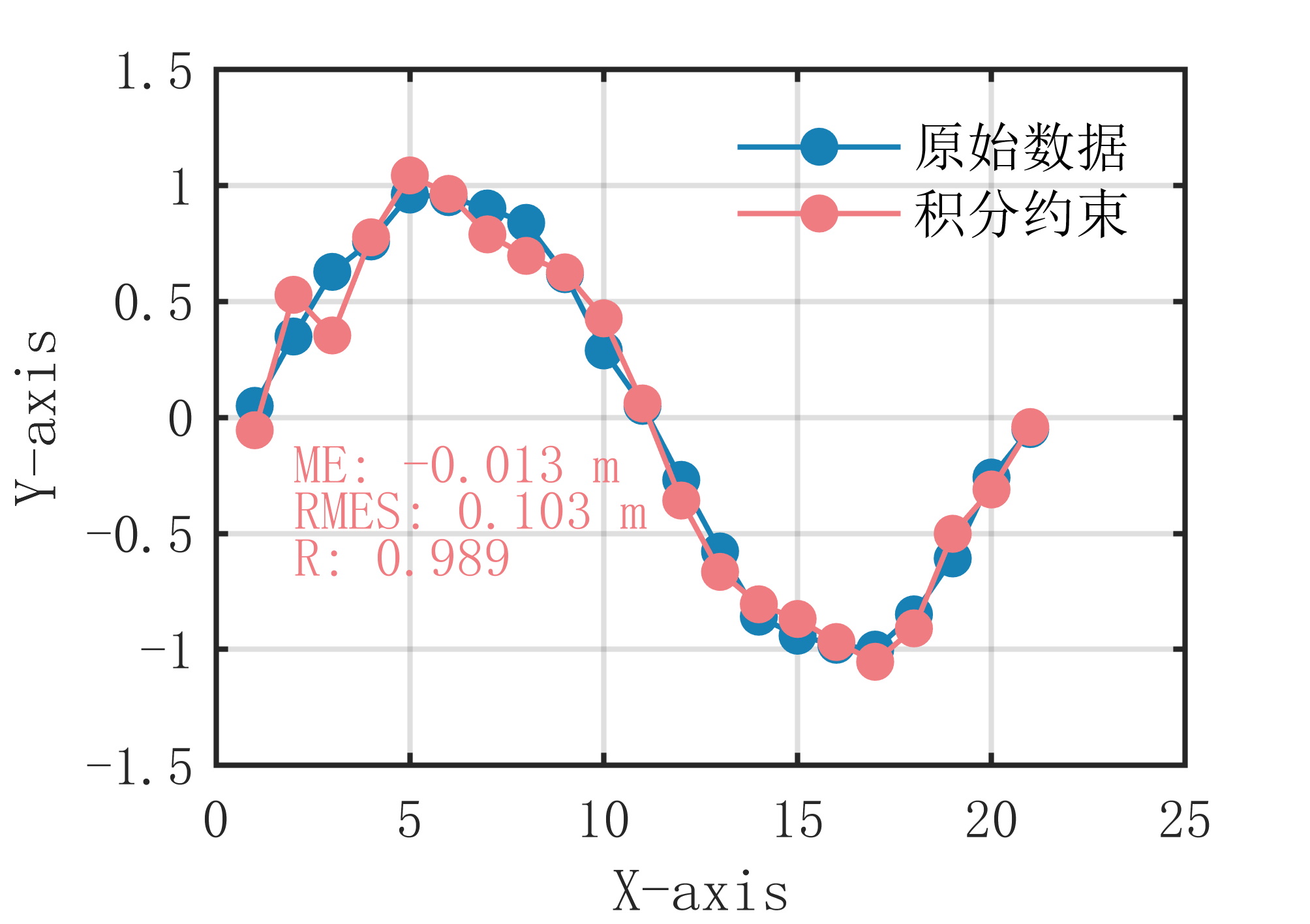
附出图效果如下：

附视频教程操作：