一、背包问题

背包问题模型及测试集简介_IT猿手的博客-CSDN博客

参考文献：

[1]耿亚,吴访升.基于粒子群-模拟退火算法的背包问题研究[J].控制工程,2019,26(05):991-996.

二、能量谷优化算法

能量谷优化算法（Energy valley optimizer，EVO）是MahdiAzizi等人于2023年提出的一种新颖的元启发式算法，其灵感来自关于稳定性和不同粒子衰变模式的物理原理。点击下方链接查看EVO原理：

能量谷优化算法（Energy valley optimizer，EVO）

三、能量谷优化算法求解背包问题

部分Matlab代码：

% 背包问题，共包含9个数据集，修改Function_name即可测试不同数据集
close all
clear 
clc
SearchAgents_no=30; % 种群大小
Function_name='F1'; %F1-F9
Max_iteration=100; % 最大迭代次数
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);%获取数据集信息
[fMin,bestX,curve]=EVO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%算法求解
ShowResult;%显示结果

部分结果：

3.1数据集1求解结果

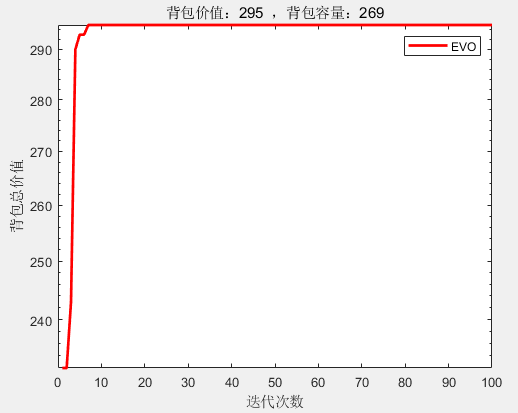
所求得的背包总价值 : 295

背包的理论最大容量 : 269

所求得的背包的容量 : 269

算法选取的物品序号 : 2  3  4  8  9 10

算法选取的物品质量 : 4 60 32 62 65 46

算法选取的物品价值 : 10 47  5 61 85 87

3.2数据集2求解结果

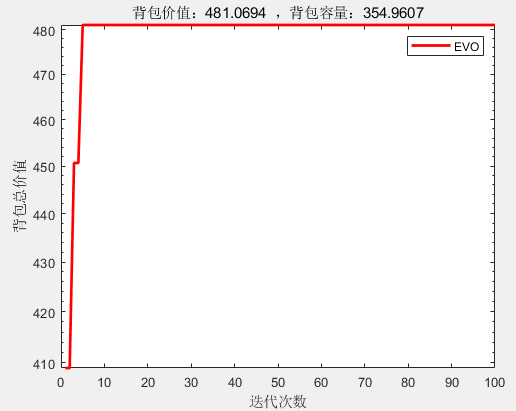
所求得的背包总价值 : 481.0694

背包的理论最大容量 : 375

所求得的背包的容量 : 354.9607

算法选取的物品序号 : 3  5  7  8 10 11 12 14 15

算法选取的物品质量 : 47.9873   74.6605   51.3535   1.49846   16.5899   44.5692    0.4669   57.1184   60.7166

算法选取的物品价值 : 58.5009    82.284   71.0501   30.3995   14.7313   98.8525   11.9083   53.1663   60.1764

3.3数据集3求解结果

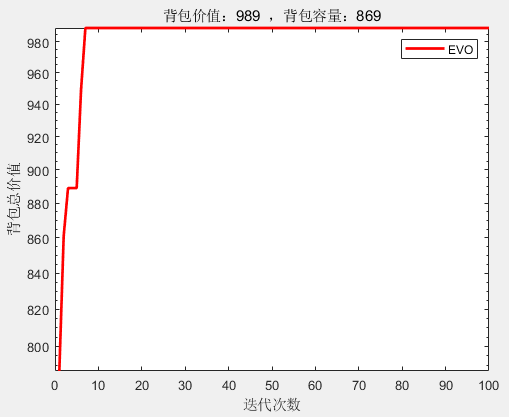
所求得的背包总价值 : 989

背包的理论最大容量 : 878

所求得的背包的容量 : 869

算法选取的物品序号 : 2  3  4  5  6  7  8 10 11 12 13 15 16 17 19 20

算法选取的物品质量 : 4 43 83 84 68 92 82 44 32 18 56 25 96 70 14 58

算法选取的物品价值 : 46 90 72 91 40 75 35 54 78 40 77 61 17 75 75 63

四、参考代码

文件夹内包含9个背包问题的所有Matlab代码，点击main.m即可运行。