一、珍鲹优化算法

珍鲹优化算法（Giant Trevally Optimizer，GTO）由HAVAL TARIQ SADEEQ和ADNAN MOHSIN ABDULAZEEZ于2022年提出，该算法模拟珍鲹狩猎海鸟时的独特行为，思路新颖。

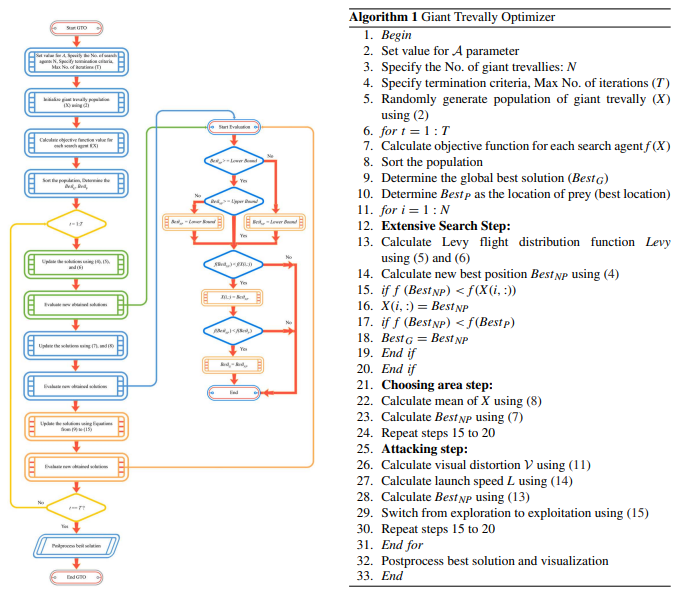
参考文献：H. T. Sadeeq and A. M. Abdulazeez, "Giant Trevally Optimizer (GTO): A Novel Metaheuristic Algorithm for Global Optimization and Challenging Engineering Problems," in IEEE Access, vol. 10, pp. 121615-121640, 2022, doi: 10.1109/ACCESS.2022.3223388.

二、小波神经网络WNN

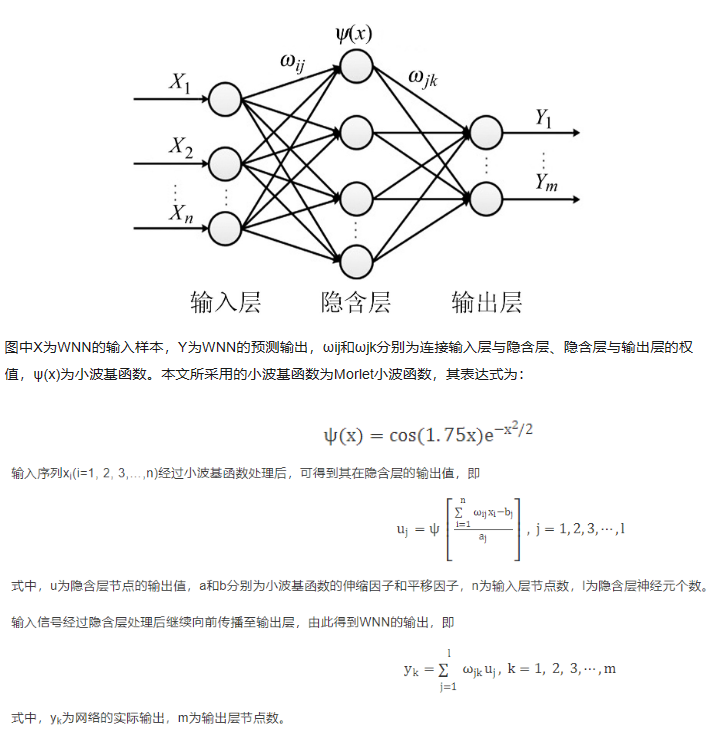
WNN是一种以小波基函数为隐含层节点、激励函数误差反向传播的神经网络，如下图所示：

三、数值实验

小波神经网络WNN中待优化参数为：输入层与隐含层的权值、小波基函数的伸缩因子、小波基函数的平移因子、隐含层与输出层的权值。珍鲹优化算法GTO的个体由WNN中输入层与隐含层的权值、小波基函数的伸缩因子、小波基函数的平移因子、隐含层与输出层的权值构成，目标函数为均方误差MSE。构建结构为5-8-2的小波神经网络WNN，通过GTO优化WNN结构参数，使其MSE最小。

部分数据如下：前5列为输入，后2列为输出

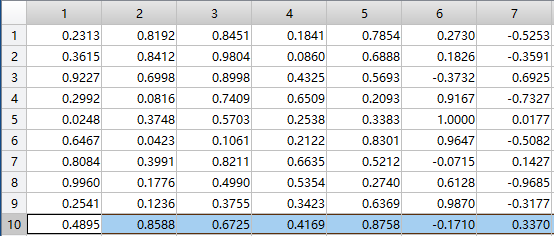
部分代码如下：WNN隐藏层神经元个数可以自己修改

close all
clear
clc
global inputnum hiddennum outputnum TrainNum 
inputnum=5;%神经网络输入层神经元个数（输入样本维度）
hiddennum=8;%神经网络隐藏层神经元个数（可以自己修改） 
outputnum=2;%神经网络输出层神经元个数（输出样本维度）
TrainNum=100;%训练集数目 
%% GTO优化小波神经网络WNN，目标函数是均方误差MSE
SearchAgents_no=30; %  种群大小（可以修改）
Function_name='F1'; 
Max_iteration=100; %  最大迭代次数（可以修改）
[lb,ub,dim,fobj]=fun_info(Function_name);% 在fun_info.m中可以查看上下限及目标函数
[fMin,bestX,curve]=GTO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);  %bestX是WNN的最优参数
save bestX bestX %保留算法优化WNN得到的最佳参数
%%
save curve curve %保留曲线
%% 画出算法优化WNN的均方误差随迭代次数的图
figure
semilogy(curve,'Color','g')
title('Objective space')
xlabel('Iteration');
ylabel('MSE');
%axis tight
grid on
box on
legend('GTO')
%%
display(['The best solution obtained is : ', num2str(bestX)]);
display(['The best optimal value of the objective funciton   is : ', num2str(fMin)]);%fMin越小说明算法优化WNN效果越好

求解结果如下：

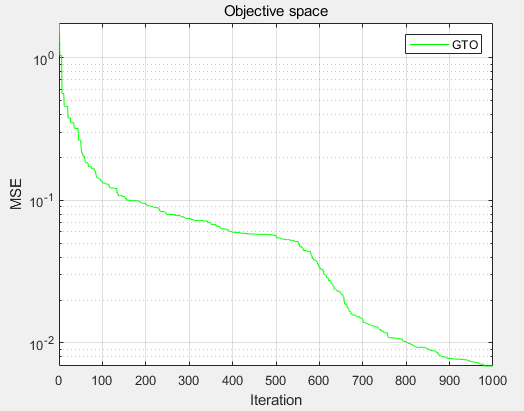
MSE收敛图：

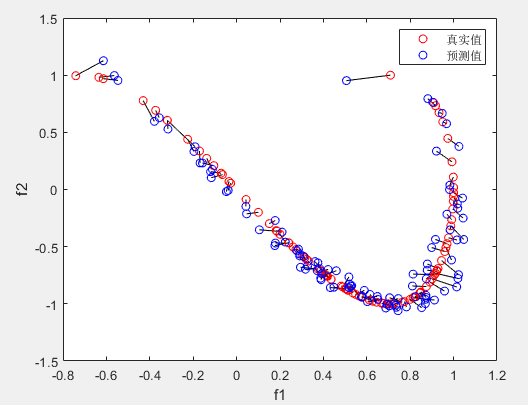
两个目标真实值与预测值：红色为真实值，蓝色为预测值，真实值与预测值用黑线连接，一一对应。

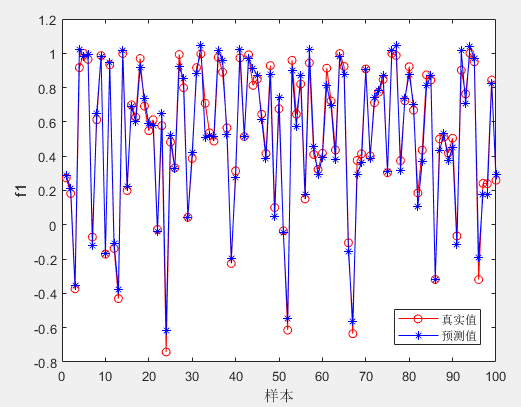
目标1真实值与预测值：

目标2真实值与预测值：

两个目标真实值与预测值的绝对误差MAE：

由此可见珍鲹优化算法GTO优化WNN用于数据预测效果十分不错，设置合适的隐藏层神经元个数，加大种群规模和迭代次数效果更佳。

四、参考代码