两天没更,除了吃吃喝喝,那就是复现了一下这篇文章的创新点,本身是传统工科-测绘学科,自然也是对高等测量平差等数据处理理论比较感兴趣,阅读文献过程中,恰好看到了这样一篇文章,于是就花了两天时间尽力复现了一下。
1 文章简介
文章 DOI: 10.1016/j. Asr.2022.10.014
链接: https://www.sciencedirect.com/science/article/abs/pii/S0273117722009358?via%3Dihub
该篇文章讲的是一种遥感反演雪深的新方法,在对每日诸多雪深反演值进行取值的过程中,应用了抗差估计的新算法获取抗差估计值,同时抗差估计值与中值以及平均值等方法进行对比。虽然相关作者没有开源抗差估计算法的代码,但是其理论讲解的很清晰完善,完全可以做到复现。
2、什么是抗差估计算法呢?
抗差估计算法(Robust Estimation)是在存在数据异常值的情况下,通过一定的统计方法来估计数据的真实值的方法。常见的抗差估计算法包括:最小二乘估计、中位数估计、M估计、LMS估计等。 最小二乘估计是一种常见的线性回归方法,它通过最小化数据的残差平方和来估计数据的真实值,但是在存在数据异常值的情况下,最小二乘估计容易受到影响。 中位数估计是一种基于数据的中位数来估计数据的真实值的方法,它对数据异常值的影响相对较小,但是在数据分布不均匀的情况下,中位数估计也容易受到影响。 M估计是一种基于极大似然估计的方法,通过对数据的似然函数进行最大化来估计数据的真实值,可以较好地抵抗数据异常值的影响。 LMS估计是一种基于最小绝对误差的方法,通过最小化数据的绝对误差来估计数据的真实值,对于存在数据异常值的情况下,LMS估计也可以得到较为准确的结果。 总的来说,抗差估计算法可以有效地提高数据的鲁棒性,提高数据分析的准确性和可靠性。
3、其应用的学科领域有哪些呢?
通常情况下,各个学科都是适用的。比如 10 个测量值,要求平均值,中值作对比的话,那也可以求抗差估计值用于对比。
应用途径:一组测雪深的20个测量值,用中值、平均值和抗差估计值三种方法对比不同方法的精度。抗差估计算法需要预先输入初始值,初始值为中值或者平均值(目前只有这两种选项哦)进行抗差估计算法研究的。
4、复现效果
原作者用的雪深值,那这里代码我也自己制作了几个雪深值用于数据处理和分析。主要是用抗差 M 估计进行复现的。
假设一组测雪深的数据 snow 为:
14.6 cm、16.8 cm、9.4 cm、9.5 cm、9.8 cm
10.7 cm、10.9 cm、9.4 cm、9.9 cm、10.8 cm
10.9 cm、10.2 cm、10.4 cm、10.5 cm、9.5 cm
10.3 cm、10.1 cm、9.6 cm、9.2 cm、10.6 cm
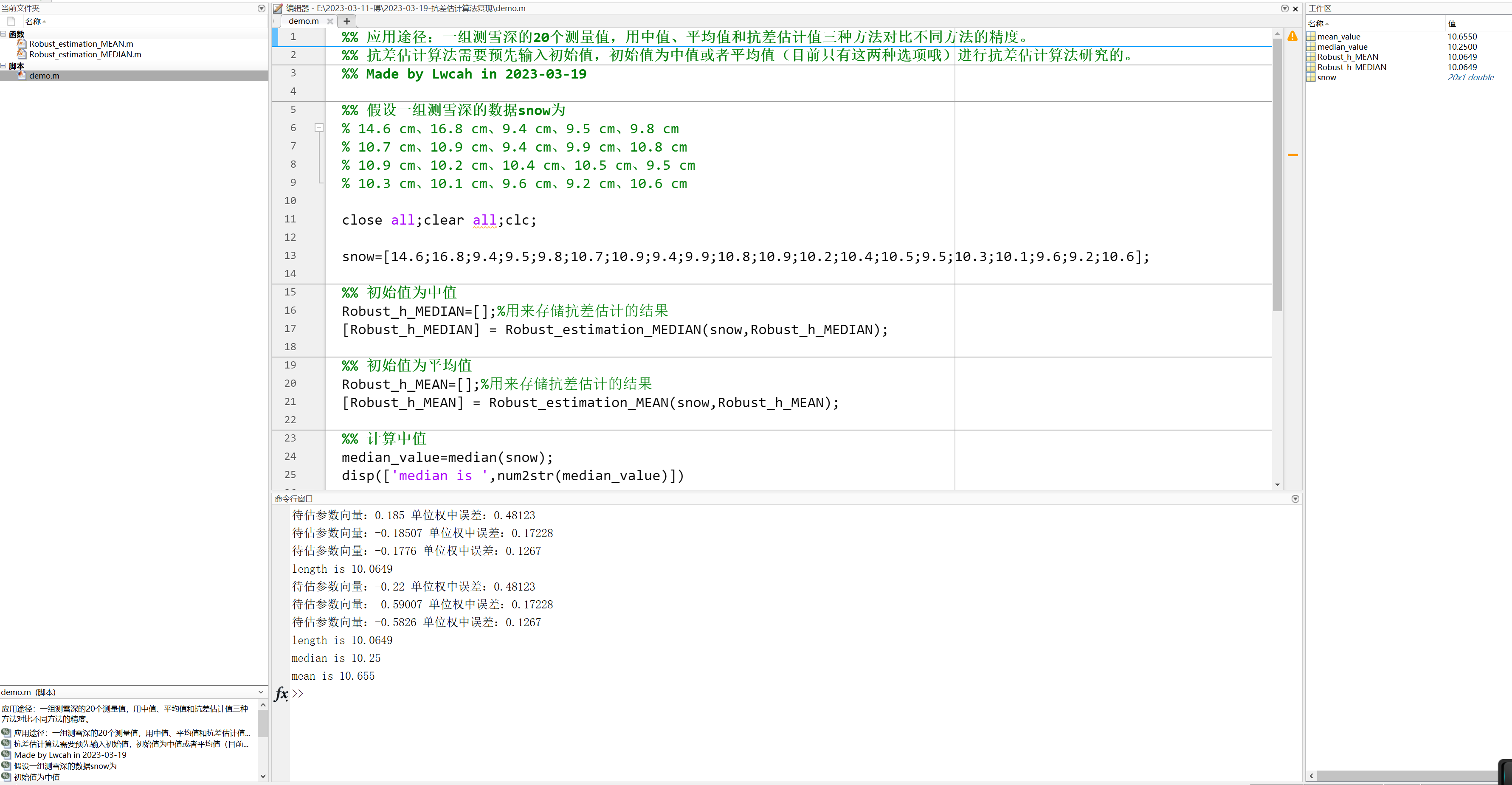
通过下方命令行输出内容可以发现:
初始值为中值和平均值的抗差估计算法求得的值为 10.0649 和 10.0649
该组雪深数据的中值为 10.25
该组雪深数据的平均值为 10.655
注:抗差估计值的目的是为了抵抗粗差的存在,当原始序列数据中存在偏差较大的数据的时候,他的应用效果会偏好。
5 附视频教程