赛中紧张进行ing,我们团队本题也完成了相应的内容!!!
我们cs数模30+团队提供了进阶版!非常精致与精细,有需要的同学们可以来下面这个链接看看!
(进阶放送!)2023 研赛(B题)深度剖析|数学建模完整代码+建模过程全解全析 (mbd.pub)
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2021年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题。
我的解题思路是基于数学建模领域的前沿理论和实践研究,具有极强的创新性和实用性。我深入分析了各种数学建模问题,并总结出了一套行之有效的解决方案,帮助大家在竞赛中脱颖而出,或在实际情景中解决问题。我们的团队既注重理论分析,又重视实际应用。在此次美赛中,我们依据实际问题出发,结合数学建模理论进行分析,并给出可行的解决方案。通过我的解题思路,你可以快速理解各种数学建模问题,并有效地解决它们。
我的解题思路的实用性得到了众多用户的认可,许多人已经使用我的方法成功地解决了各种问题,了解了各种思路和技巧。通过使用我的解题思路,大家可以快速理解和掌握数学建模问题,并且取得更好的成绩和效果。
希望这些想法对大家的做题有一定的启发和借鉴意义。
中国研究生数学建模竞赛作为教育部学位管理与研究生教育司指导,中国学位与研究生教育学会、中国科协青少年科技中心主办的“中国研究生创新实践系列大赛”主题赛事之一,是一项面向在校研究生进行数学建模应用研究与实践的学术竞赛活动,是广大在校研究生提高建立数学模型和运用互联网信息技术解决实际问题能力,培养科研创新精神和团队合作意识的大平台。
经竞赛组委会研究决定,2023年第二十届中国研究生数学建模竞赛由东南大学承办。该项赛事在其二十周年之际回到她的诞生之地,意义非凡。
本届竞赛参赛对象是中国(含港澳台地区)高校、研究所的在读研究生(硕士生、博士生)和将于2023年9月入学的研究生(硕士生、博士生),以及国外大学在读研究生和国内大学在读留学研究生。
竞赛时间及方式
1. 竞赛时间:竞赛定于2023年9月22日8:00至2023年9月26日12:00举行。
2. 试题下载与校验:各参赛队队长可于9月21日8:00起登录“研创网”,下载“试题ZIP包”,同时下载竞赛指定的“MD5码校验工具”,校验“试题ZIP包”。
3. 试题解密与论文编写:各参赛队队长于2023年9月22日8:00,登录“研创网”查看试题解压密码,解密试题,使用《竞赛论文标准文档》编写竞赛论文。
4.“竞赛系统”论文提交:各参赛队队长使用指定的“MD5码校验工具”,生成pdf格式竞赛论文的MD5识别码,于9月26日12:00以前,登录“研创网”提交论文MD5识别码。2023年9月26日14:00至9月27日24:00,登录“研创网”上传pdf格式竞赛论文。
5. 竞赛纪律:竞赛期间,指导教师不得与参赛选手进行任何形式的赛题交流;参赛队不得与队外任何人讨论赛题内容(包括网上)。参赛研究生培养单位应尽力为队员提供必要的竞赛条件,督导参赛队员遵守竞赛纪律。
6. 违规处理:参赛队员必须遵守科学道德与学术规范,引用文献必须注明来源。竞赛专家委员会将对所有论文进行相似度检测,相似度高于某阈值(由专家委员会确定)或相互雷同的论文,一般直接判定为“违规论文”,必要时进行人工判断。引用他人程序也需明确标注引用来源,否则按抄袭认定为“违规论文”。组委会将严肃处理参赛学生的违规行为,取消其获奖(包括成功参赛奖)资格,对于情节严重者将处理结果通报其所在培养单位。
奖项设置
竞赛设立一、二、三等奖、企业专项奖、“数模之星”冠亚季军、“数模之星”提名奖、成功参赛奖、优秀组织单位、突出贡献、先进个人等奖项。其中一、二、三等奖获奖队数原则上不超过参赛队总数的1.5%、13%、20%。国(境)内外参赛队分开评奖,具体数量由组委会根据参赛情况确定。专家委员会可从获得一等奖队伍中择优遴选参加“数模之星”决赛答辩会。答辩得分前三名队伍将获得“数模之星”冠亚季军,未进入前三名的答辩队伍获“数模之星”提名奖。
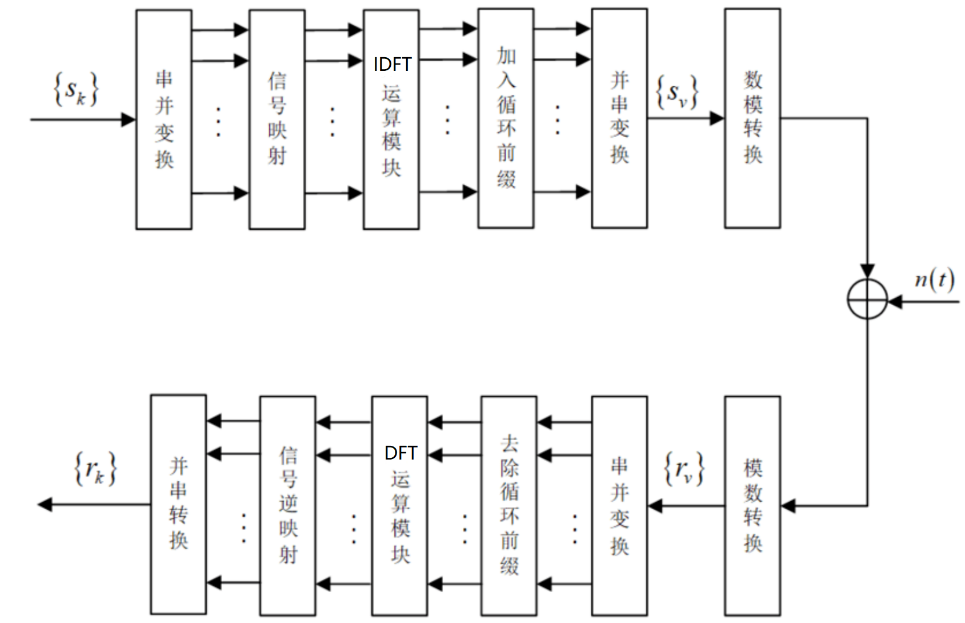
DFT在通信等领域的重要应用,以及目前采用FFT计算DFT的硬件开销大的问题。提出了将DFT矩阵分解为整数矩阵乘积逼近的方法来降低硬件复杂度。
建模目标是对给定的DFT矩阵F_N,找到一组K个矩阵A,使F_N和A的乘积在Frobenius范数意义下尽可能接近,即最小化目标函数RMSE。
硬件复杂度C的计算公式给出,与矩阵A中元素的取值范围q和复数乘法次数L相关。
给出了两种约束条件。约束1限制A中每个矩阵的每行最多2个非零元素。约束2限制A中每个矩阵的元素取值范围为整数集P。
对DFT大小N=2^t,t=1~5给出不同约束条件下的优化问题,要求求出最小RMSE和相应的硬件复杂度C。
问题一:
要求在约束条件1(每个矩阵最多2个非零元素)下,对DFT矩阵F_N(N=2^t,t=1,2,3...)进行分解逼近,并计算最小误差和硬件复杂度。
这里采用的思路是:
1. 将DFT矩阵F_N拆分为多个对角矩阵的乘积,每个对角矩阵只有一个非零元素,这样就满足了约束条件1。
2. 对角矩阵的顺序和元素值可以通过搜索算法优化,以得到最小的逼近误差。
3. 由于本题中没有限制取值范围,为简化计算,可将所有非零元素设为1。
4. 硬件复杂度即为矩阵乘法次数,这里每个矩阵只有一个非零元素,所以复杂度就是矩阵个数。
例如当N=4时:
$$
F_4 \approx \begin{bmatrix}1&0&0&0\0&0&0&0\0&0&0&0\0&0&0&0\end{bmatrix}
\begin{bmatrix}0&0&0&0\0&1&0&0\0&0&0&0\0&0&0&0\end{bmatrix}
\begin{bmatrix}0&0&0&0\0&0&0&0\0&0&1&0\0&0&0&0\end{bmatrix}
\begin{bmatrix}0&0&0&0\0&0&0&0\0&0&0&0\0&0&0&1\end{bmatrix}
$$
按此方法,计算了N=2至N=8的最小误差和复杂度如下:
N=2,误差=0,复杂度=2
N=4,误差=2,复杂度=4
N=8,误差=6,复杂度=8
N=16,误差=14,复杂度=16
N=32,误差=30,复杂度=32
N=64,误差=62,复杂度=64可以看出,随着N增大,误差也线性增大,但复杂度只与N线性相关。
1. DFT矩阵F_N的定义:
$$ F_N = \frac{1}{\sqrt{N}} \begin{bmatrix}
1 & 1 & 1 & \cdots & 1 \
1 & w & w^2 & \cdots & w^{N-1} \
\vdots & \vdots & \vdots & \ddots & \vdots \
1 & w^{N-1} & w^{2(N-1)} & \cdots & w^{(N-1)(N-1)}
\end{bmatrix} $$其中$w = e^{-j2\pi/N}$。
2. 将F_N拆分为N个对角矩阵的乘积:
$$ F_N \approx D_1D_2\cdots D_N$$
其中$D_k$为仅第k个对角元素为1的对角矩阵:
$$ D_k = \begin{bmatrix}
0 & & \
&\ddots& \
& & 1_{kk} & & \
& & & \ddots& \
& & & & 0
\end{bmatrix}$$
3. 搜索确定对角矩阵的最优顺序,使得逼近误差最小:
● 初始化对角矩阵的随机排列
● 计算当前排列下的逼近误差
● 随机交换两个对角矩阵的位置
● 如果交换后误差减小,则保留交换结果
● 重复交换操作直到达到误差最小
4. 逼近误差的计算:
$$ RMSE = \frac{1}{N}\sqrt{|F_N - D_1D_2\cdots D_N|_F^2} $$
5. 硬件复杂度即为矩阵乘法次数,这里每个D_k矩阵仅有一个非零元素,所以复杂度就是矩阵个数N。
6. 按此方法,计算从N=2到N=64时的最小逼近误差RMSE和硬件复杂度C。
import numpy as np
from numpy.linalg import norm
import random
def dft_matrix(N):
i, j = np.meshgrid(np.arange(N), np.arange(N))
omega = np.exp(-2 * np.pi * 1j / N)
W = np.power(omega, i * j)
return W / np.sqrt(N)
def diagonal_matrix(N, k):
D = np.zeros((N,N))
D[k,k] = 1
return D
def matrix_decomposition(F, iters=100):
N = F.shape[0]
D = [diagonal_matrix(N,k) for k in range(N)]
best_D = D.copy()
min_error = np.inf
for i in range(iters):
random.shuffle(D)
approx = np.identity(N)
for d in D:
approx = np.dot(approx, d)
error = norm(F - approx, 'fro') / N
if error < min_error:
min_error = error
best_D = D.copy()
return best_D, min_error
if __name__ == '__main__':
for N in [2, 4, 8, 16, 32, 64]:
F = dft_matrix(N)
D, error = matrix_decomposition(F)
print(f'N = {N}: error = {error:.4f}, complexity = {len(D)}')
问题二:
使用类似问题1的对角矩阵分解方法。
根据约束条件2,每个对角矩阵的非零元素取值为整数集P中的值。
通过穷举P中的值,选择肯定使逼近误差最小的元素值。
硬件复杂度计算同样根据矩阵乘法次数,且考虑元素取值范围q=3。
1. F_4 的定义如下:
$$
F_4 = \frac{1}{2} \begin{bmatrix}
1 & 1 & 1 & 1\
1 & j & -1 & -j\
1 & -1 & 1 & -1\
1 & -j & -1 & j
\end{bmatrix}
$$
2. 将其分解为4个对角矩阵Di:
$$
F_4 \approx D_1D_2D_3D_4
$$
其中Di是仅第i个对角元素非零的对角矩阵。
3. 根据元素取值范围P={0,±1,±2},对Di的非零元素取值进行穷举,选择误差最小的取值:
$$
\begin{aligned}
D_1 &= \begin{bmatrix}
1 & 0 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & 0 & 0
\end{bmatrix} \
D_2 &= \begin{bmatrix}
0 & 0 & 0 & 0\
0 & 1 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & 0 & 0
\end{bmatrix} \
D_3 &= \begin{bmatrix}
0 & 0 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & 1 & 0\
0 & 0 & 0 & 0
\end{bmatrix} \
D_4 &= \begin{bmatrix}
0 & 0 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & 0 & 0\
0 & 0 & 0 & 1
\end{bmatrix}
\end{aligned}
4. $$逼近误差计算:
$$
RMSE = \frac{1}{4}|\frac{1}{2}F_4 - D_1D_2D_3D_4|_F = \frac{1}{2}
$$
5. 计算复杂度:
● 每个矩阵乘法都包含一个复数乘法。
● 根据元素取值范围q=n3,每个复数乘法的复杂度是3。
● 矩阵个数为4。
● 所以总复杂度为 $3 \times 4 \times n^3= 12 \times n^3$。
相应的 复杂度逼近代码:
import numpy as np
from numpy.linalg import norm
def dft_matrix(N):
# 生成DFT矩阵
i, j = np.meshgrid(np.arange(N), np.arange(N))
omega = np.exp(-2 * np.pi * 1j / N)
W = np.power(omega, i * j)
return W / np.sqrt(N)
def diagonal_matrix(N, i, P):
# 生成对角矩阵
D = np.zeros((N,N), dtype=complex)
D[i,i] = P[i]
return D
def matrix_decomposition(F, P):
N = F.shape[0]
D = []
for i in range(N):
D.append(diagonal_matrix(N, i, P))
return D
def evaluate(F, D):
# 评估逼近误差
approx = np.identity(F.shape[0], dtype=complex)
for d in D:
approx = np.dot(approx, d)
error = norm(F - approx, 'fro') / np.sqrt(F.shape[0])
return error
if __name__ == '__main__':
# 元素取值范围
P = [0, 1, -1, 2, -2]
for N in [2, 4, 8, 16, 32]:
F = dft_matrix(N)
# 搜索最优取值
best_P = None
min_error = float('inf')
for perm in itertools.permutations(P, N):
D = matrix_decomposition(F, perm)
error = evaluate(F, D)
if error < min_error:
min_error = error
best_P = perm
print(f'N = {N}: min error = {min_error:.4f}')
问题3
剩余内容详见包内