0.引言
上一篇博客介绍了使用Yalmip工具箱求解单阶段鲁棒优化的方法。这篇文章将和大家一起继续研究如何使用Yalmip工具箱求解两阶段鲁棒优化(默认看到这篇博客时已经有一定的基础了,如果没有可以看看我专栏里的其他文章)。关于两阶段鲁棒优化与列与约束生成算法的原理,之前的博客已经详细地介绍过了,这里就不再过多介绍,主要是结合实例来讲解编程思路。这篇博客用到了两个算例,1个是两阶段鲁棒优化问题和列与约束生成算法的开山鼻祖[1],另一个是电气专业中两阶段鲁棒优化问题最热门的文章之一[2],相信大家在网上见到过无数号称完美复现的代码,但实际上大部分都是有问题的(包括我自己早期写的代码,也是被网上的代码带歪了,后面理解慢慢深入才发现问题所在)。
求解两阶段鲁棒优化问题一共有两个难点,一是求解max-min或者min-max形式的子问题,其实就是求解一个单阶段鲁棒优化,上一篇博客我已经非常详细地介绍了求解方式,借助Yalmip工具箱,共有三种不同的方式可以解决。二是主问题和子问题的迭代求解,也就是列与约束生成算法(C&CG)的实现。很多代码在复现C&CG算法时并没有向主问题同时添加列(变量)和约束,这也是代码中最常见的问题。针对这两个难点,我将用两个不同的算例详细地进行讲解。
此外,文献[1]和[2]中都是采用了先将约束条件写成紧凑的矩阵形式,然后再对子问题进行处理的方式,很多朋友和我反映这部分太难处理了,实际问题的约束建模过程中经常包括循环语句,想要转成矩阵形式确实很不容易。这篇文章中我将分别采用两种不同的方式求解鲁棒优化。一是采用原始的约束条件,省去将约束条件转为矩阵形式的步骤,这种方式数学公式可能会更繁琐,但比起矩阵形式的转换,理解起来会更容易一些。二是采用矩阵形式进行编程,在博客中我教大家一种非常简单就能将约束写为矩阵形式的方法,文中只是介绍了如何使用,之后也会单独写博客对此详细展开。
总之,这篇博客干货满满,可以认真通读一遍,跟着博客中的思路亲自动手使用Matlab+ Yalmip实现两阶段鲁棒优化的编程(博客中提到的所有例子我都提供了相应的代码)。相信大家理解后,面对任何类型的两阶段鲁棒优化问题都能迅速使用类似的方法进行解决。
博客中主要包含8大内容:
①.拿到一个复杂的两阶段鲁棒优化问题的分析步骤和方法。
②.采用Yalmip工具箱中的uncertain函数和鲁棒优化模块求解两阶段鲁棒优化的子问题。
③.Yalmip工具箱中的鲁棒优化模块和常规的求解思路有什么异同。
④.使用KKT条件求解两阶段鲁棒优化的子问题,并使用C&CG算法进行迭代求解。
⑤.使用对偶变换求解两阶段鲁棒优化的子问题,并使用C&CG算法进行迭代求解。
⑥.采用Yalmip工具箱的内置函数,将线性约束写成紧凑矩阵形式的方法。
⑦.矩阵形式的两阶段鲁棒优化问题,如何快速写出子问题内层优化的KKT条件,并使用C&CG算法进行迭代求解。
⑧.矩阵形式的两阶段鲁棒优化问题,如何快速写出子问题内层优化的对偶问题,并使用C&CG算法进行迭代求解。
1.两阶段鲁棒优化基本形式
如文献[1]中所述,标准的两阶段鲁棒优化问题的形式为:
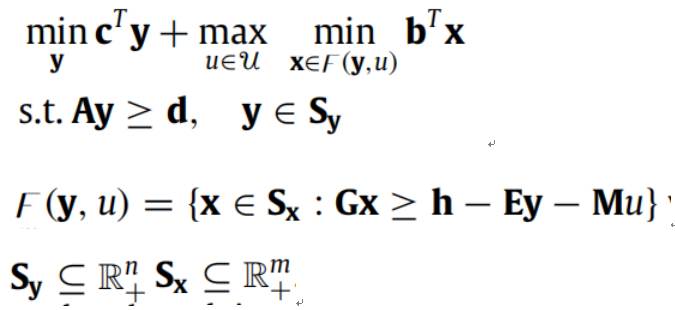
其中,y为第一阶段决策变量,u为不确定变量,x为第二阶段决策变量。和分析单阶段鲁棒优化问题的五个特征一样,拿到一个复杂的两阶段鲁棒优化问题先不用慌,按照下面的步骤进行分析即可:
1)确定第一阶段决策变量有哪些,将其与变量y对应。
2)确定第二阶段决策变量有哪些,将其与变量x对应。
3)确定不确定变量有哪些,将其与变量u对应。
4)确定优化问题中不确定集合的形式,并考虑是否可以直接使用Yalmip中的鲁棒优化模块进行求解。
5)确定目标函数是否有仅包含第一阶段决策变量的项,如果有的话可以单独拿出来。
6)确定子问题的目标函数,将其与鲁棒优化的标准形式相对应。
7)确定约束条件,考虑是否包含非线性约束,是否需要线性化。
8)求解max-min或者min-max类型的子问题。
9)使用迭代方式,将子问题产生的变量和约束不断添加到主问题中,最终得到最优解。
下面分别以文献[1]和[2]中的优化问题进行讲解说明:
2.两阶段鲁棒运输问题编程实战
文献[1]中算例分析部分运输问题的两阶段鲁棒优化模型如下:
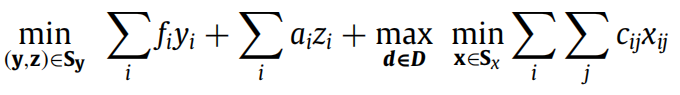
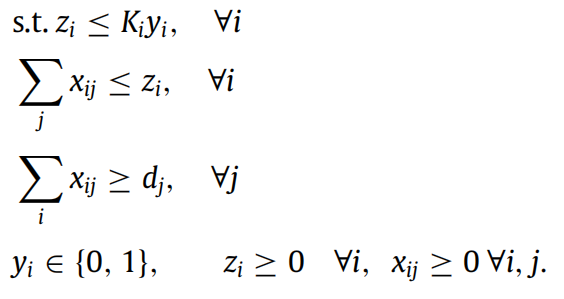
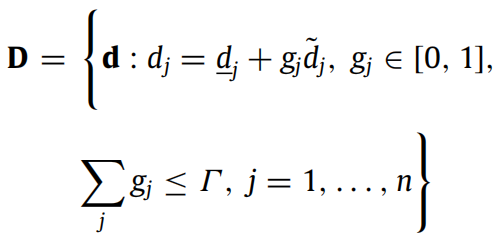
我之前写过一篇博客解析这篇论文,但是使用的是紧凑的矩阵形式。由于该问题比较简单,紧凑形式和一般约束形式差别不大,这次博客将使用一般形式的约束进行求解,方便大家体会两阶段鲁棒优化原理。
2.1 鲁棒优化模块求解
按上面的思路逐步进行分析:
1)确定第一阶段决策变量有哪些。
第一阶段决策变量为y和z,其中yi是m维的0-1变量,取1时表示在i地建造仓库,z是m维的连续变量,表示仓库的容量(m是待选址仓库的数目)。
2)确定第二阶段决策变量有哪些。
第二阶段决策变量为xij,是一个m×n的连续变量,表示从i仓库运往j用户的商品数目(n是用户数)。
3)确定不确定变量有哪些。
不确定变量为dj,表示j用户的不确定商品需求。
4)确定优化问题中不确定集合的形式,并考虑是否可以直接使用Yalmip中的鲁棒优化模块进行求解。
该优化问题的不确定集中为多面体形式,可以直接使用Yalmip中的鲁棒优化模块进行求解。
5)确定目标函数是否有仅包含第一阶段决策变量的项,如果有的话可以单独拿出来。
目标函数中有一部分仅包含第一阶段的决策变量,第二阶段子问题的目标函数可以不考虑这部分。
6)确定子问题的目标函数,将其与两阶段鲁棒优化的标准形式相对应。
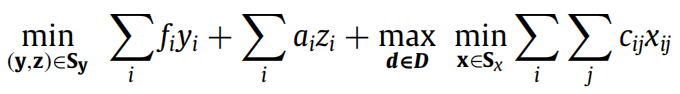
其中子问题的目标函数为:
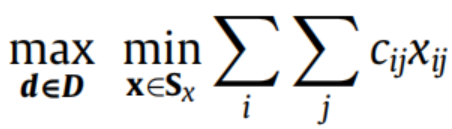
7)确定约束条件,考虑是否包含非线性约束,是否需要线性化。
子问题中的约束条件均为线性,且决策变量中不包含0-1变量,满足强对偶定理,KKT条件和对偶变换都是适用的。可以直接通过uncertain函数直接使用Yalmip鲁棒优化模块。
分析完成后,下面可以开始尝试求解子问题,相关参数如下:

需要注意的是,为了子问题的模型可行,需要保证三个仓库容量的总和大于用户最高的需求(也就是当g0+g1+g2=1.8时的用户需求),也就是需要添加约束条件:
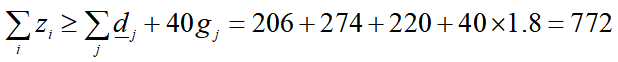
根据上面的公式,我们可以写出各个参数矩阵以及变量的表达式:
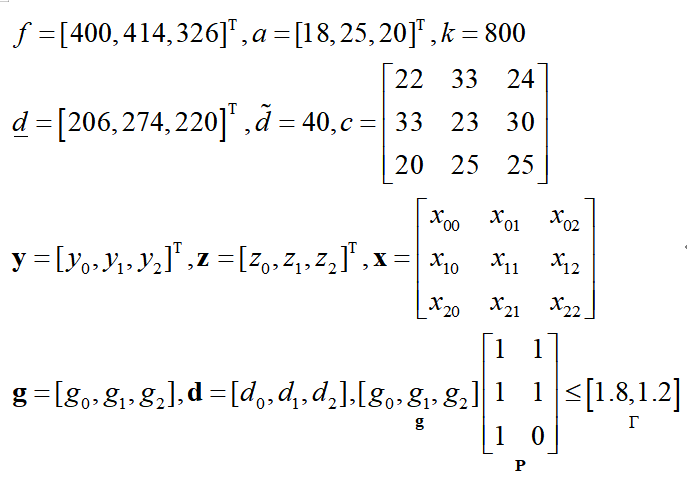
用matlab代码表示如下:
%% 参数矩阵
f = [400; 414; 326];
a = [18; 25; 20];
k = 800;
C = [22, 33, 24;
33, 23, 30;
20, 25, 27];
d_ = [206; 274; 220];
d_wave = 40;
gamma = [1.8,1.2];
P = [1 1;1 1;1 0];
%% 决策变量
y = binvar(3,1);
z = sdpvar(3,1);
x = sdpvar(3,3,’full’);
d = sdpvar(3,1);
g = sdpvar(3,1);
%% 目标函数
objective = f'*y + a'*z + sum(sum(C.*x));
%% 约束条件
Constraints = [];
Constraints = [Constraints , z >= 0 , x >= 0 , g >= 0 , g <= 1];
Constraints = [Constraints , z <= k*y , sum(z) >= sum(d_) + gamma(1)*d_wave];
Constraints = [Constraints , sum(x) <= z'];
Constraints = [Constraints ,sum(x,2) >= d];
Constraints = [Constraints ,d == d_ + g*d_wave];
Constraints = [Constraints ,g'*P <= gamma];
%% 设置求解器
ops = sdpsettings('verbose', 3, 'solver', 'gurobi');
sol = optimize(Constraints,objective,ops);
可以先尝试求解一下确定性优化问题,和后面的两阶段鲁棒优化进行对比:

8)求解max-min或者min-max类型的子问题。
为了便于调试,我们首先把子问题给解决了,再通过迭代求解两阶段鲁棒优化问题。其中在子问题中,第一阶段的变量y和z实际都是已知量,此时子问题可以转为:
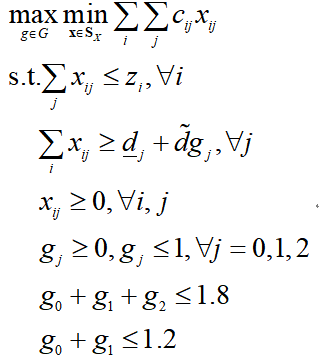
注意,我在模型中通过等式约束,消去了决策变量d,并使用决策变量g来表示不确定性,减少变量的数目,加快求解效率。
此外,由于子问题中可以将主问题的决策变量视为常数,因此只含有变量y,z的约束都可以省略,如果变量x的约束中带有变量y,z,那么视为常数即可。为了子问题调试方便,我们先把确定性优化结果中z的取值为[772;0;0],并带入求解子问题,求解成功了再和主问题进行交互迭代,Matlab代码如下:
%% 两阶段鲁棒优化的子问题—采用鲁棒优化模块求解
clc
clear
close all
warning off
%% 参数设置
f = [400; 414; 326]; % 仓库建设费用
a = [18; 25; 20]; % 单位容量存储费用
C = [22, 33, 24; % 从仓库i到用户j的单位运输费用
33, 23, 30;
20, 25, 27];
d_ = [206; 274; 220]; % 基准用户需求
d_wave = 40; % 需求波动
gamma = [1.8,1.2]; % 不确定预算
P = [1 1;1 1;1 0]; % 不确定集合的系数矩阵
%% 决策变量
z = [772;0;0]; % 仓库的容量
x = sdpvar(3,3,'full'); % 从仓库i到用户j运输的商品数
g = sdpvar(3,1); % 用户需求的波动幅度
%% Objective
objective = sum(sum(C.*x));
%% 约束条件
G = [uncertain(g) , g'*P <= gamma , g >= 0 , g <= 1 ];
Constraints = [];
Constraints = [Constraints , sum(x,2) <= z ,x >= 0 ];
Constraints = [Constraints , sum(x)' >= d_ + g*d_wave];
%% 求解优化问题
ops=sdpsettings('verbose', 3, 'solver', 'cplex' );
sol=optimize(Constraints + G , objective ,ops);
%% 判断求解是否成功
if sol.problem == 0
disp('求解成功!!!');
else
disp(['求解失败,原因为',sol.info]);
end
%% 优化结果
if sol.problem == 0
objective = value(objective)
y = [1;0;1]
x = value(x)
z = value(z)
F = f'*y + a'*z + sum(sum(C.*x))
end
运行结果如下:
![]()
结果显示优化问题不可行,无法使用Yalmip的鲁棒优化模块进行求解。但是按照官方文档说法,是可以使用鲁棒优化模块求解的,针对这个问题,我去询问了YALMIP工具箱的作者Johan Löfberg教授,他的回复是这样的:


按照老师的说法,Yalmip中的鲁棒优化模块考虑的并不是求出一种最恶劣场景下的决策方案,而是求出所有可能最恶劣的场景下都能满足约束条件的一种决策方案。
老师给了一个例子:
x <= w,y <= 1-w,x+y>=0.5
其中w是不确定变量,对于任意一种相对恶劣的场景,这个问题是具有可行解的。例如w=0,w=1,但是鲁棒优化模块求解的方案要求对所有可能最恶劣的场景,决策变量都要满足约束条件,因此w=0时的约束条件(x<=0,y<=1),与w=1时的约束条件(x<=1,y<=0)都要满足,也就是x<=0,y<=0,和另一个约束条件x+y>=0.5互相冲突,因此这个简单的鲁棒优化实例是没有可行解的。编程验证一下:
%% Johan Löfberg教授提供的例子
clc
clear
sdpvar x y w
objective = x + y;
Constraints = [uncertain(w) , w >= 0 , w <= 1];
Constraints = [Constraints , x <= w , y <= 1 - w , x + y >= 0.5];
ops = sdpsettings('verbose', 3, 'solver', 'cplex');
sol = optimize(Constraints,objective,ops);
if sol.problem == 0
disp('求解成功');
else
disp(['求解失败,错误原因为:',sol.info]);
end
运行结果:
![]()
显然,这两个鲁棒优化无法使用Yalmip鲁棒优化模块求解的原因是一样的。都是任意一种最恶劣的场景都具有可行解,但是无法在所有可能的恶劣场景下具有可行解。
了解了问题的本质之后,我们可以知道,Yalmip鲁棒优化模块的求解结果和我们的要求其实是不太一样的。但如果想使用Yalmip鲁棒优化模块求解,需要做如下考虑:
问题其实就是当仓库的总容量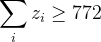 时,肯定是可以满足任意一种恶劣的场景(即对于变量d任意的取值,都可以得到可行解),但无法满足所有可能的场景(即使它们不会同时发生,就和例子中的w=0和w=1不会同时发生一样)。如要考虑所有可能场景,则需要仓库的总容量更大,即:
时,肯定是可以满足任意一种恶劣的场景(即对于变量d任意的取值,都可以得到可行解),但无法满足所有可能的场景(即使它们不会同时发生,就和例子中的w=0和w=1不会同时发生一样)。如要考虑所有可能场景,则需要仓库的总容量更大,即:
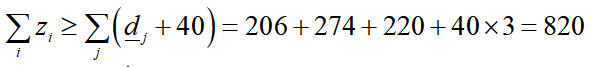
将这个约束条件到确定性优化中,得到一个可行解,其中z的取值为[546;0;274],再带入子问题中,进一步得到求解结果:

我们得到了鲁棒优化模块的求解结果,但这个结果和文献[1]中所提的优化问题并不完全等价,因此求解两阶段鲁棒优化时并不推荐使用这种方法。假设我们要做的是单阶段鲁棒优化,使用Yalmip的鲁棒优化模块可以快速得到结果。例如将两阶段鲁棒优化改写成单阶段鲁棒优化:
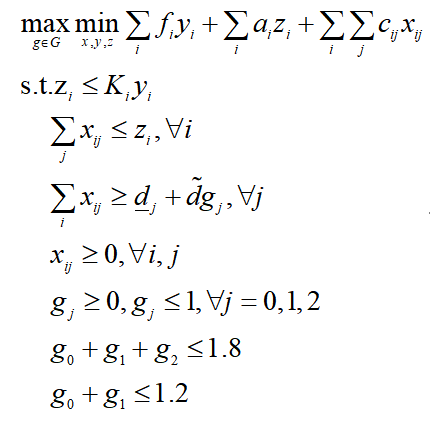
求解这个问题的matlab代码如下:
%% 单阶段鲁棒优化问题
clc
clear
close all
warning off
yalmip('clear')
%% 参数矩阵
f = [400; 414; 326];
a = [18; 25; 20];
k = 800;
C = [22, 33, 24;
33, 23, 30;
20, 25, 27];
d_ = [206; 274; 220];
d_wave = 40;
gamma = [1.8,1.2];
P = [1 1;1 1;1 0];
%% 决策变量
y = binvar(3,1);
z = sdpvar(3,1);
x = sdpvar(3,3,'full');
g = sdpvar(3,1);
%% 目标函数
objective = f'*y + a'*z + sum(sum(C.*x));
%% 约束条件
Constraints = [];
Constraints = [Constraints , z >= 0 , x >= 0 ];
Constraints = [Constraints , z <= k*y];
Constraints = [Constraints , sum(x,2) <= z];
Constraints = [Constraints , sum(x) >= (d_ + g*d_wave)'];
G = [uncertain(g) , g >= 0 , g <= 1 , g'*P <= gamma];
%% 设置求解器
ops=sdpsettings('verbose', 3, 'solver', 'gurobi');
sol=optimize([Constraints , G],objective,ops);
%% 分析错误标志
if sol.problem == 0
disp('求解成功');
else
disp(['求解失败,错误原因为:',sol.info]);
end
%% 输出结果
if sol.problem == 0
objective = value(objective)
y = value(y)
x = value(x)
z = value(z)
end
运行结果如下:
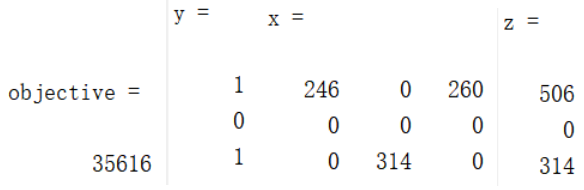
另外,由于使用KKT条件或强对偶变换的方式求解子问题后,都要采用相同的方式和主问题迭代得到两阶段鲁棒优化问题的最优解,所以我会先把两种求解方法介绍完之后,再讲解如何将主问题和子问题结合起来迭代求解。
2.2 KKT条件求解子问题
为了方便求解,我们首先把子问题的内层min优化问题写出来,并将所有约束写成≤的形式:

由于内层优化中相当于只有变量x,不确定变量g和第一阶段优化变量y可以视为常数,其拉格朗日函数为:

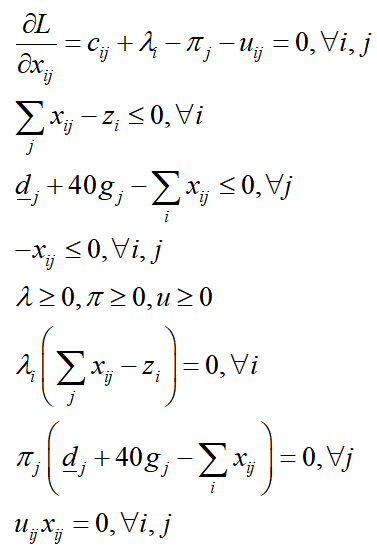
其中该优化问题的最后三项为互补松弛条件,是非线性约束,可以引入0-1变量,利用大M法进行等效线性化,过程如下:
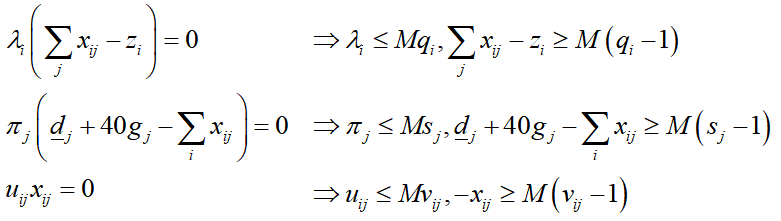
其中q为m维0-1变量,s为n维0-1变量,v为m×n维0-1变量。将内层优化的KKT方程组添加到外层优化中,就可以将双层优化问题转为单层优化问题,如下式所示:
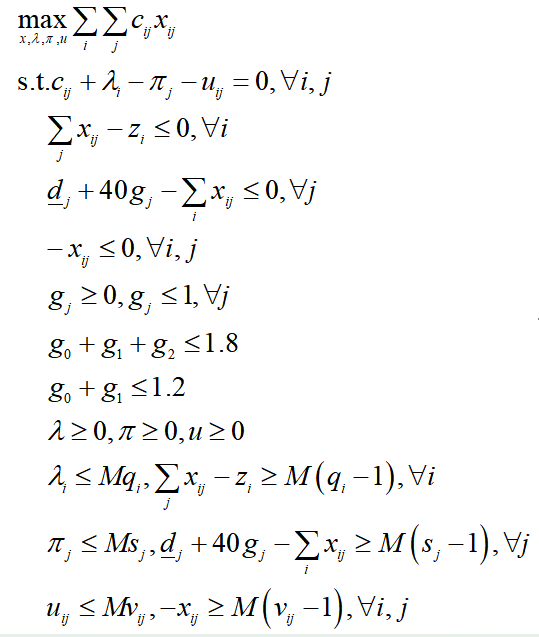
经过上面的处理,便顺利将max-min形式的子问题转为混合整数线性规划问题,并可以使用Yalmip进行求解,代码在压缩包中的Problem1文件夹中,运行Problem1_subproblem_KKT.m文件即可得到结果(假设z=[772;0;0]),运行结果如下:

使用KKT条件求解和使用鲁棒优化模块的结果略微有些不同,同时使用KKT条件求解时可以返回不确定变量的取值,即最恶劣场景下,用户的需求分别为206,274+40=314和220+0.8*40=252。
2.3 使用对偶变换求解子问题
子问题的内层优化问题为:
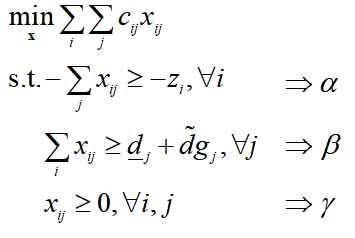
其中α,β,γ均为对偶变量,α为3×1的变量,β为1×3的变量,γ为3×3的变量,我们以挨个条件对比的方式来写对偶问题:
1)原问题为min问题,对偶问题为max问题。
2)原问题中有9个变量,因此对偶问题中有9个约束条件。
3)原问题中变量都≥0,因此对偶问题中约束条件的符号是≤0。
4)原问题中目标函数的系数cij,因此对偶问题的约束条件中≤号右边的常数也为cij。
5)原问题中有3+3+9=15个约束条件,因此对偶问题有15个决策变量。
6)原问题中约束条件的符号为≥,因此对偶问题中决策变量的取值都≥0。
7)原问题中第1个约束条件中x11,x12,x13的系数均为1,因此对偶变量α1在对偶问题9个不同的约束条件中的系数分别为[1,1,1;0,0,0;0,0,0];原问题中第2个约束条件中x21,x22,x23的系数均为-1,因此对偶变量α2在对偶问题9个不同的约束条件中的系数分别为[0,0,0;1,1,1;0,0,0];原问题中第3个约束条件中x31,x32,x33的系数均为1,因此对偶变量α3在对偶问题9个不同的约束条件中的系数分别为[0,0,0;0,0,0;1,1,1]。
8)原问题中第4个约束条件中x11,x21,x31的系数均为1,因此对偶变量β1在对偶问题9个不同的约束条件中的系数分别为[1,0,0;1,0,0;1,0,0];原问题中第5个约束条件中x12,x22,x32的系数均为1,因此对偶变量β2在对偶问题9个不同的约束条件中的系数分别为[0,1,0;0,1,0;0,1,0];原问题中第6个约束条件中x13,x23,x33的系数均为1,因此对偶变量β3在对偶问题9个不同的约束条件中的系数分别为[0,0,1;0,0,1;0,0,1]。
9)原问题中第7-15个约束条件中xij的系数均为1,因此对偶变量γij在对偶问题9个不同的约束条件中的系数均为1。
综上所述,子问题内层优化的对偶问题可以写做:
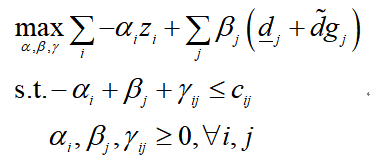
将内层优化的对偶问题和外层问题合并,得到:
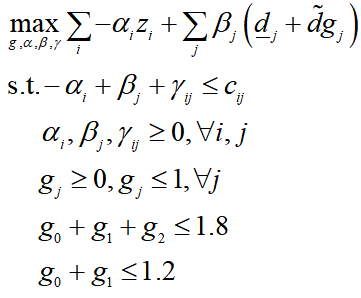
其中,目标函数中包含变量β和变量g的乘积,是一个非线性项,文献[1]的附录中假设变量g为0-1变量,则可以使用大M法进行线性化。但这种假设需要满足一定的条件,即不确定预算Γ只能为整数。当不确定预算Γ不是整数时,只能将优化问题看作一个二次规划问题,虽然是非线性优化,但也可以使用KKT条件或者求解器求解,这里我们直接使用求解器进行求解。
代码在压缩包中的Problem1文件夹中,运行Problem1_subproblem_dual.m文件即可得到结果(假设z=[772;0;0]),运行结果如下:
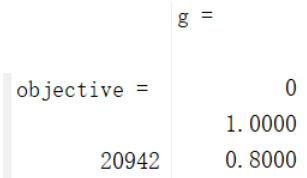
2.4 C&CG算法+KKT条件求解
2.1节到2.3节,分别采用Yalmip工具箱的鲁棒优化模块,KKT条件与对偶变换三种方法求解得到子问题。其中鲁棒优化模块求解与子问题的逻辑有一些区别。又因为子问题的对偶变换得到的是一个二次规划问题,求解速度略慢于KKT条件得到的线性规划问题,因此我们首先使用KKT条件求解子问题,并采用C&CG方法迭代求解两阶段鲁棒优化问题(如果想使用对偶变换,步骤基本相同)。
首先可以把两阶段鲁棒优化问题可以分为主问题和子问题:
KKT版本主问题MP1_KKT:
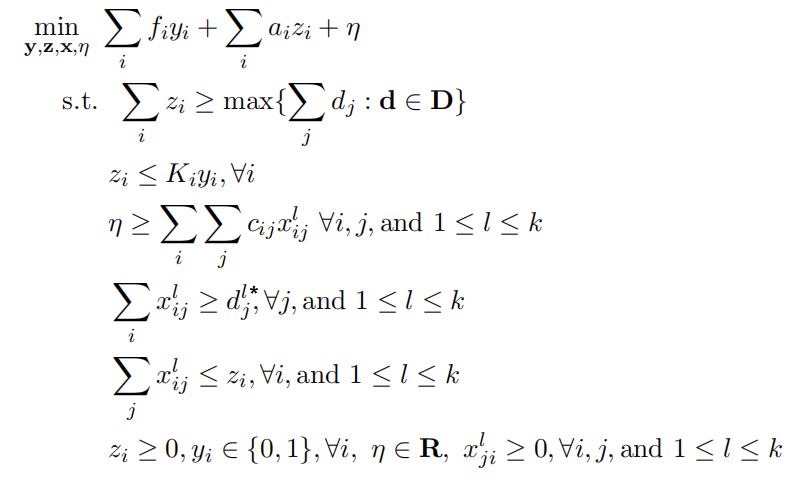

网上很多C&CG的代码,其实对C&CG算法的原理都没有理解透彻,在每次迭代过程中都是在主问题中更新而不是增加决策变量和约束条件,很容易出现迭代无法收敛的情况,就算收敛了得到的也不是最优解。
KKT条件版本子问题SP1_KKT:
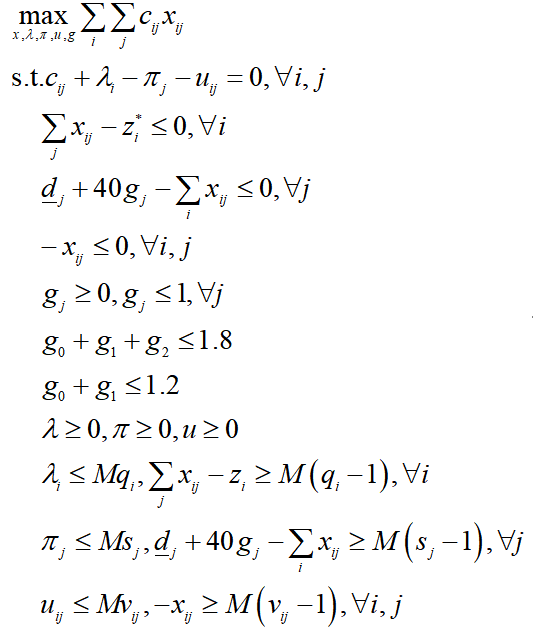
使用C&CG算法与KKT条件求解两阶段鲁棒优化的步骤概括如下:


对比可知,当子问题有解时,需要将第k次迭代时子问题的目标函数作为约束条件添加到主问题中。如果无解时,则需要相应地减少向主问题条件的约束条件。
使用KKT条件+C&CG算法求解该两阶段鲁棒优化问题的代码在压缩包中的Problem1文件夹中,运行Problem1_KKT.m文件即可得到结果,运行结果如下:

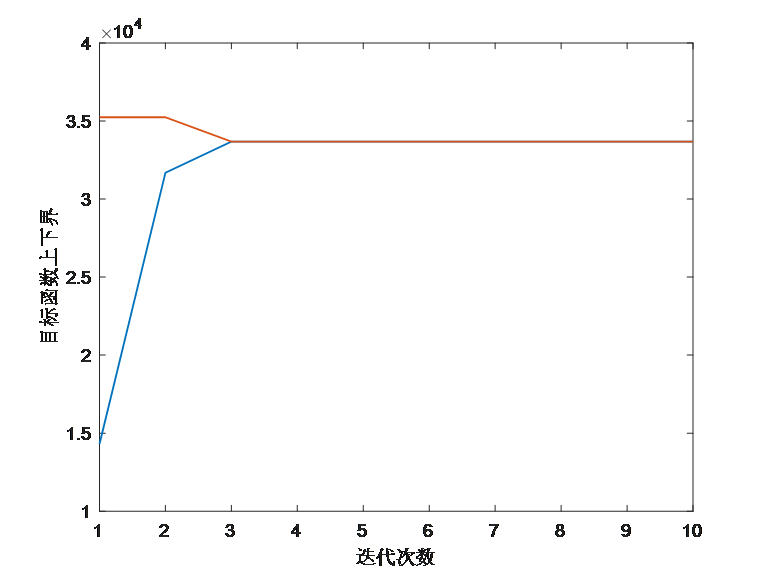
结果表明该方法可以有效求解两阶段鲁棒优化问题。
2.5 C&CG算法+对偶变换求解
首先可以把两阶段鲁棒优化问题可以分为主问题和子问题:
对偶变换版本主问题MP1_dual:
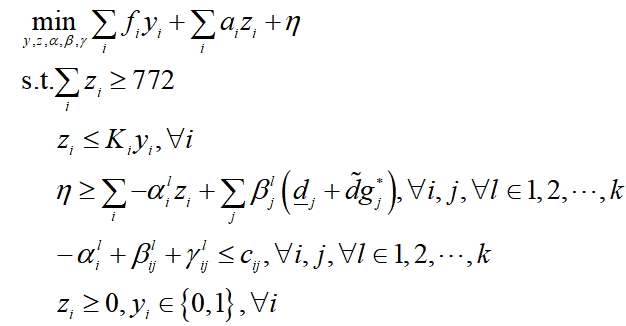
对偶变换版本子问题SP1_dual:
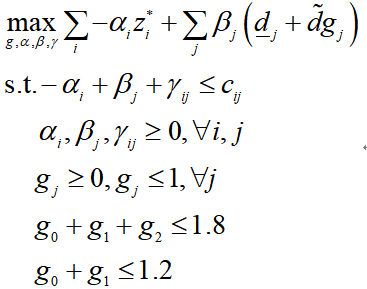
使用C&CG算法与对偶变换求解两阶段鲁棒优化的步骤概括如下:


使用对偶变换+C&CG算法求解该两阶段鲁棒优化问题的代码在压缩包中的Problem1文件夹中,运行Problem1_dual.m文件即可得到结果,运行结果如下:
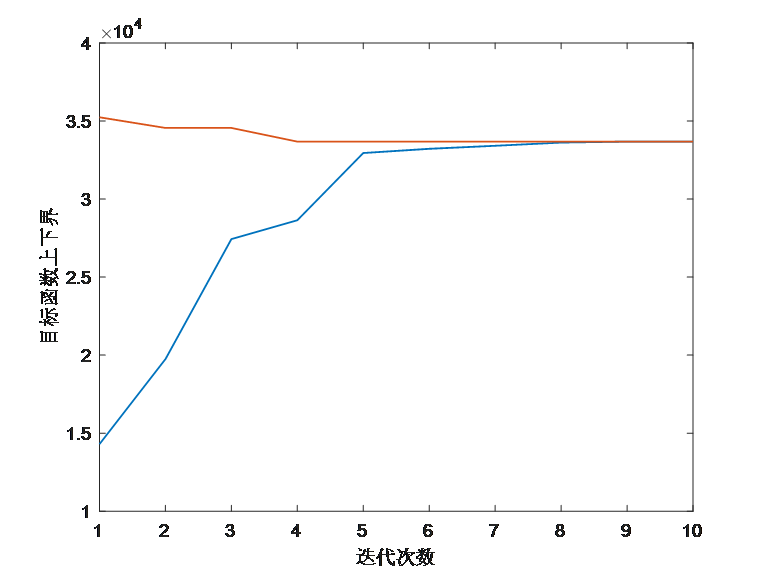

由于对偶变换引入了非线性项,所以求解效率明显低于KKT条件的求解方式。
3.微电网两阶段鲁棒优化调度编程实战
第二个算例来源于文献[2],其两阶段鲁棒优化问题的形式为:
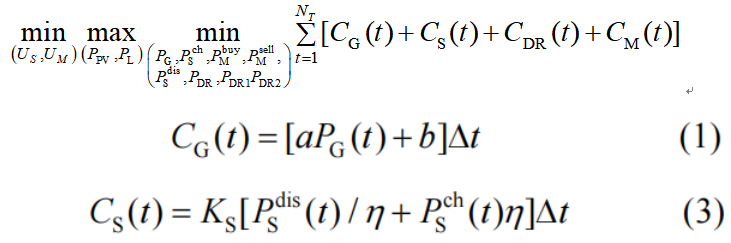
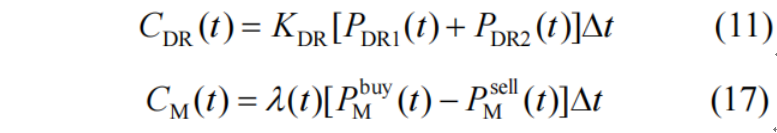
s.t.
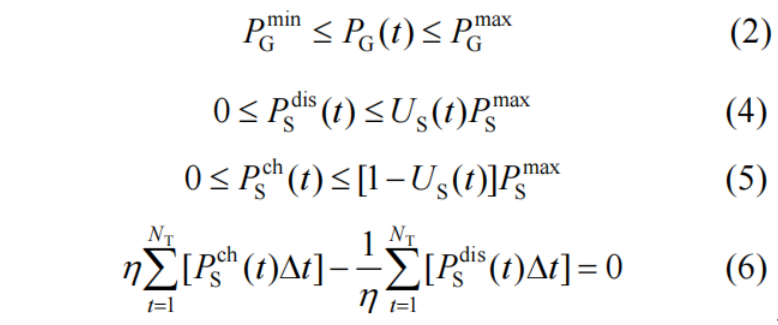
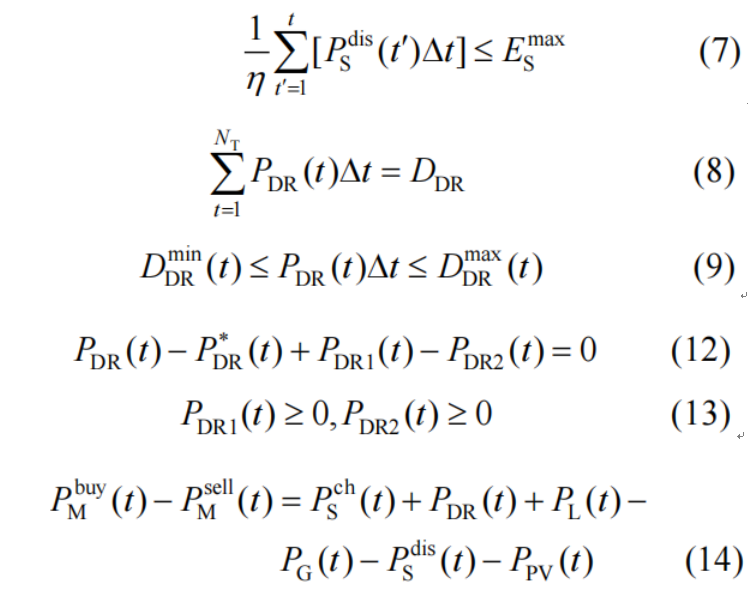
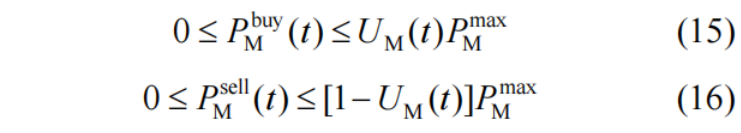
我之前写过一篇博客解析这篇论文,但是使用的是紧凑的矩阵形式。这次博客我先尝试使用一般形式的约束进行求解,方便大家体会采用矩阵形式求解两阶段鲁棒优化的方便之处。
首先逐步进行分析:
1)确定第一阶段决策变量有哪些。

2)确定第二阶段决策变量有哪些。

3)确定不确定变量有哪些。

4)确定优化问题中不确定集合的形式,并考虑是否可以直接使用Yalmip中的鲁棒优化模块进行求解。
该优化问题的不确定集中为箱式不确定集,但包含0-1变量,不可以直接使用Yalmip中的鲁棒优化模块进行求解。
5)确定目标函数是否有仅包含第一阶段决策变量的项,如果有的话可以单独拿出来。
该优化问题第一阶段和第二阶段目标函数相同。
6)确定子问题的目标函数,将其与两阶段鲁棒优化的标准形式相对应。
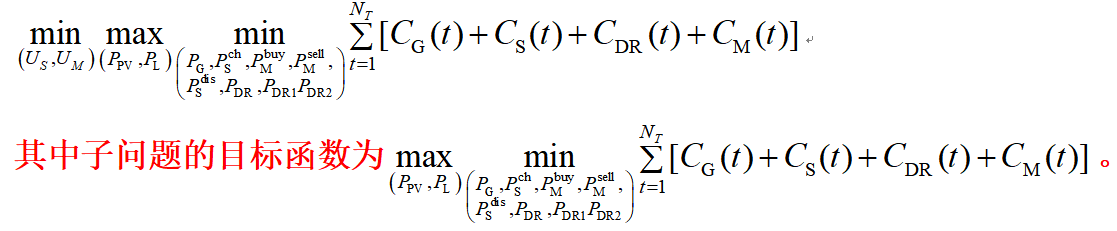
7)确定约束条件,考虑是否包含非线性约束,是否需要线性化。
子问题中的约束条件均为线性,但不确定变量的约束条件包含0-1变量,则含变量
的优化问题并不满足强对偶定理,KKT条件和对偶变换都无法适用。那是不是无法使用常规的方法求解单阶段鲁棒优化形式的子问题呢?
当然不是,如果出现这种情况,我们就可以把不确定变量写在外层。那么对于子问题的内层优化问题来说,变量是一个确定值,即使其中包含0-1变量,也只是一个常数。实际上子问题的内层优化并不包含0-1变量,因此还是可以使用常规的KKT条件或强对偶定理进行求解。但是由于不确定变量中包含0-1变量,直接通过uncertain函数直接使用Yalmip鲁棒优化模块的方法不可行。
分析完成后,分别使用KKT条件和强对偶定理求解子问题,具体如下:
3.1 KKT条件求解子问题
为了方便求解,我们首先把子问题的内层min优化问题写出来,并将所有约束写成≤0的形式或=0的形式:


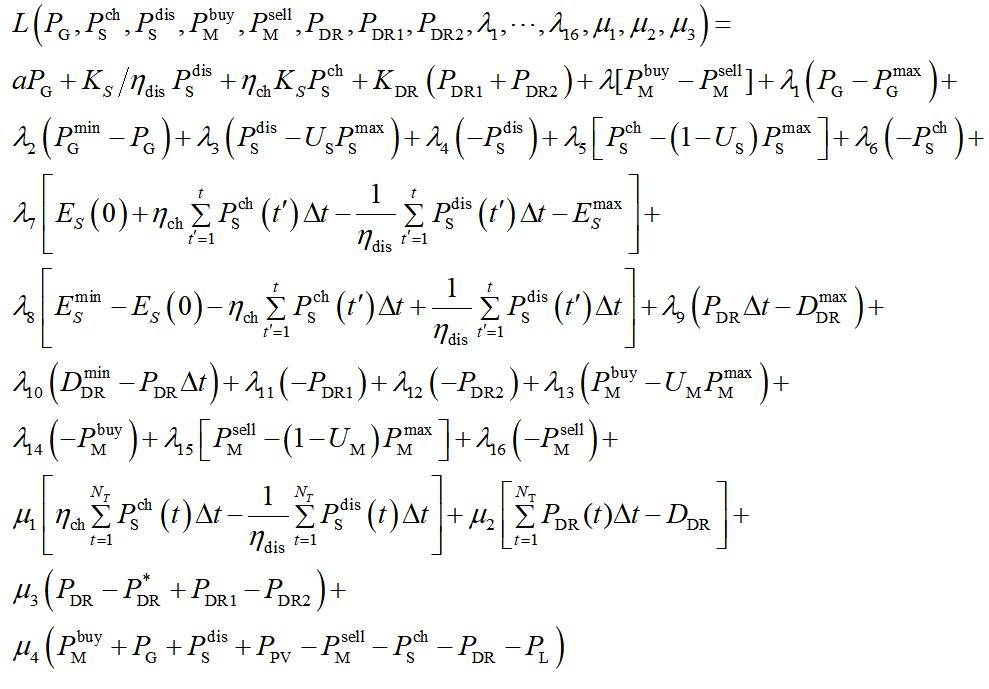
根据拉格朗日函数可以写出内层优化的KKT条件。
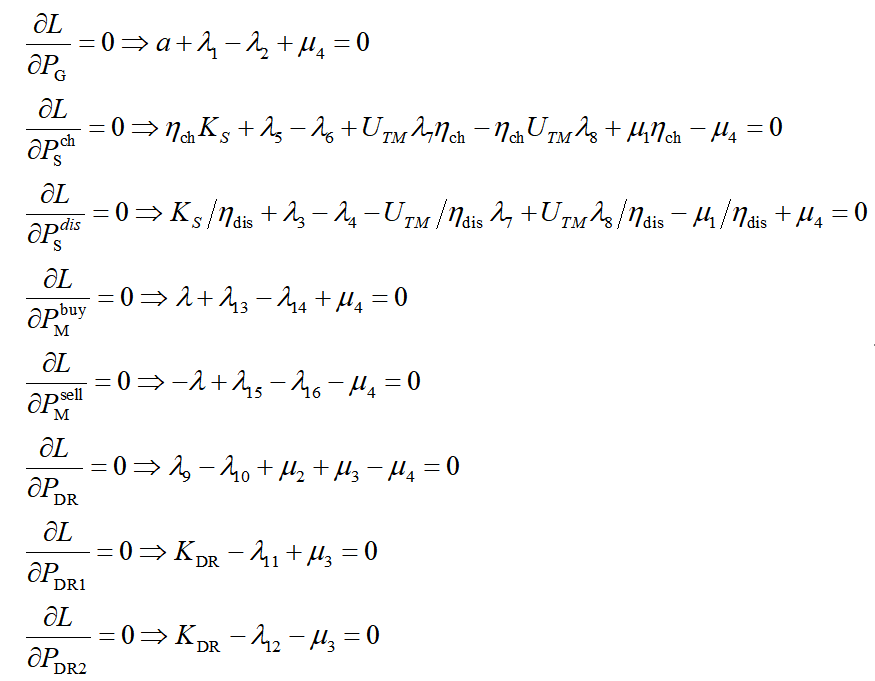
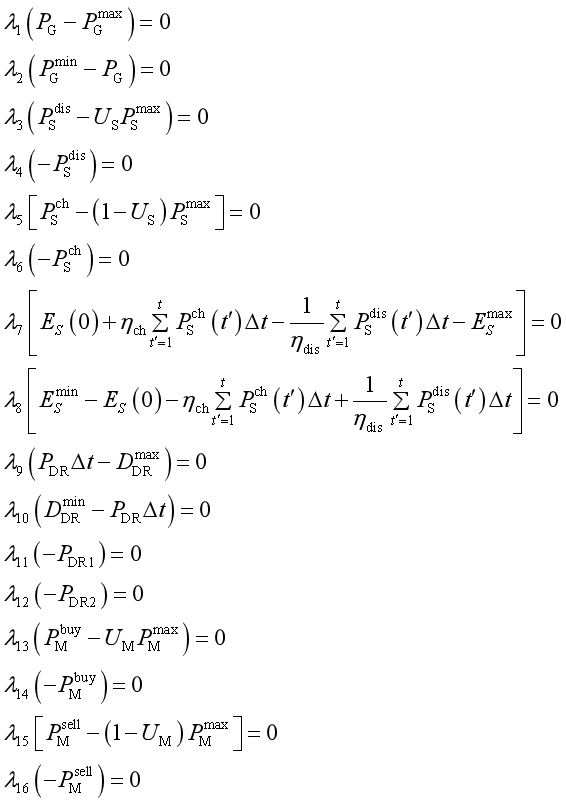
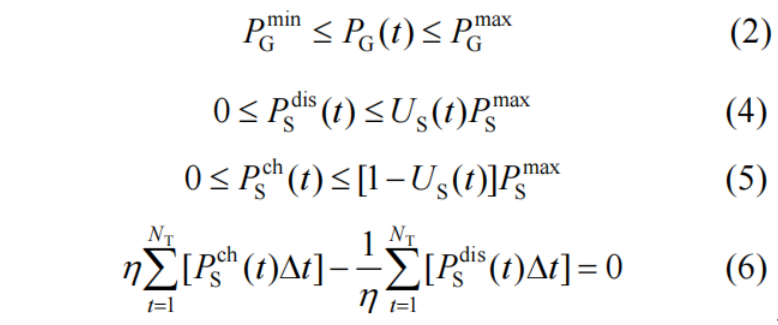
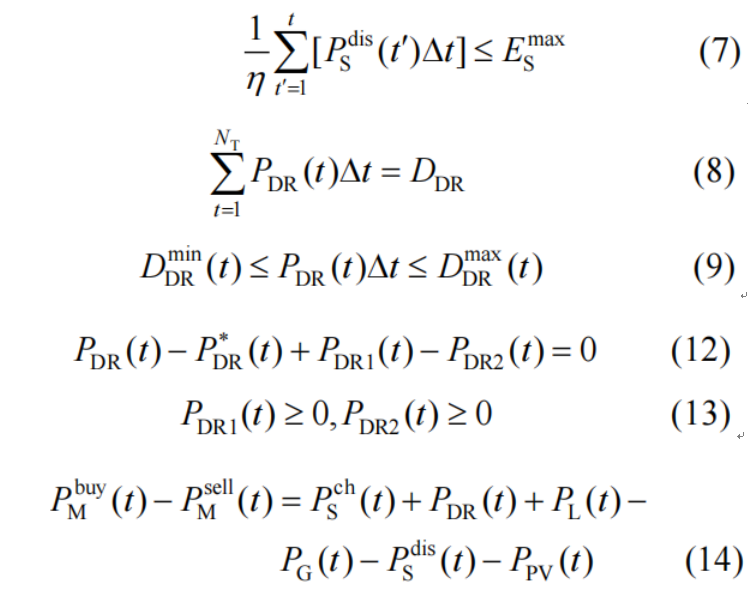
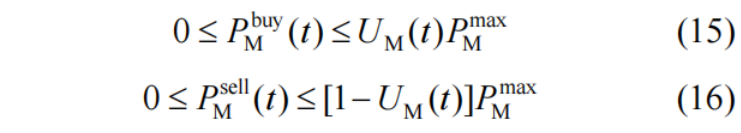
其中表示上三角全为1,主对角线以下全为0的24阶方阵,即:
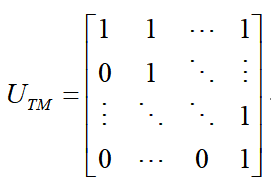
要想求解这个问题,还需要写出引入16组0-1变量,使用大M法将16组互补松弛条件转为线性约束,具体如下:
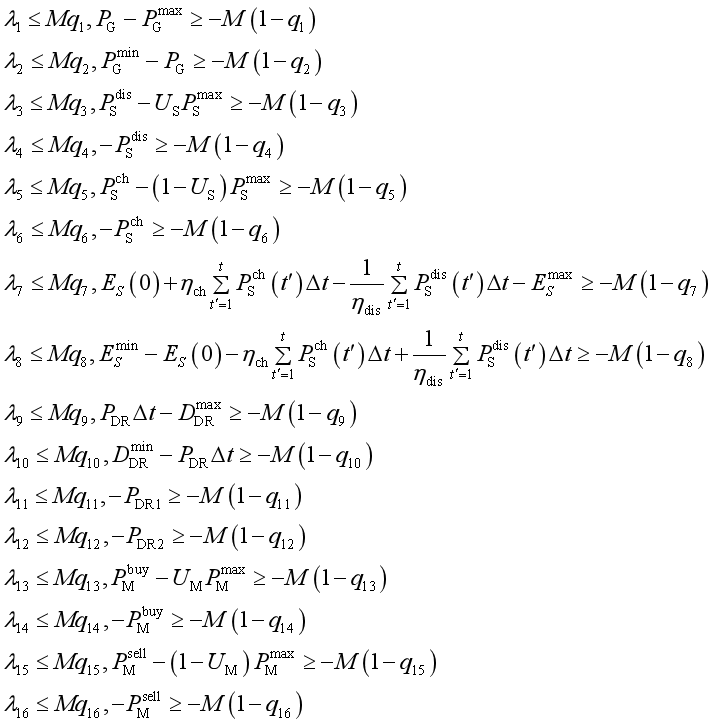
其中q1-q16都是0-1变量,qi和λi的维度相同。
将内层优化的KKT方程组添加到外层优化中,就可以将双层优化问题转为单层优化问题。经过上面的处理,便顺利将max-min形式的子问题转为混合整数线性规划问题,并可以使用Yalmip进行求解,代码在压缩包中的Problem2文件夹中,运行Problem2_subproblem_KKT1.m文件即可得到结果。
PS:假设第一阶段变量的取值:
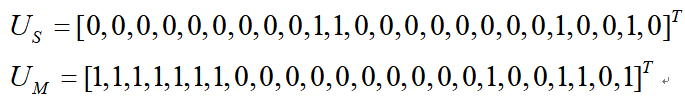
运行结果如下:
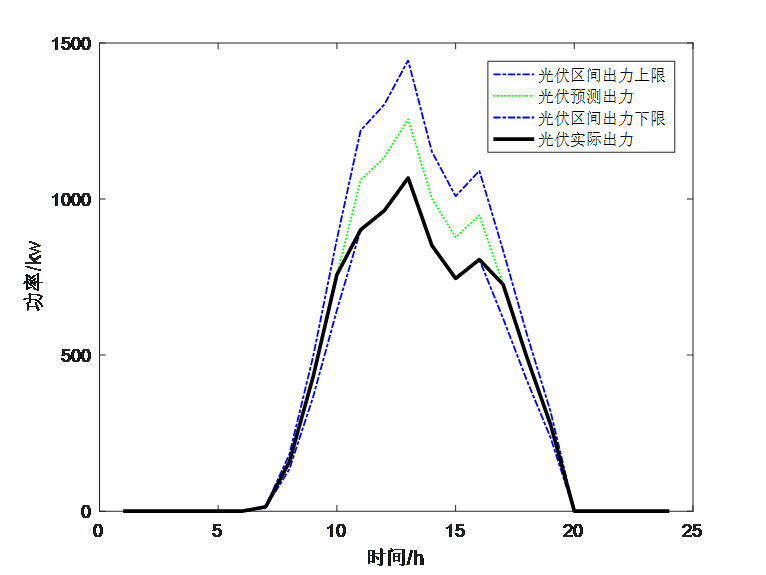
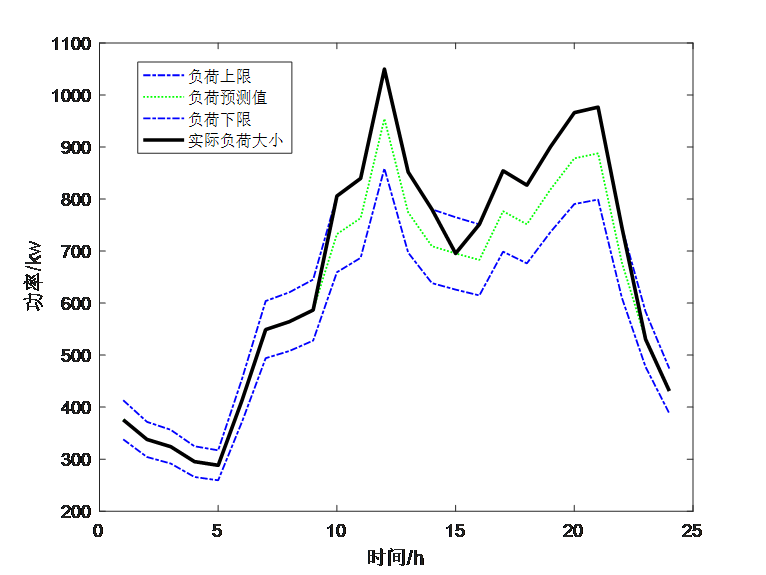
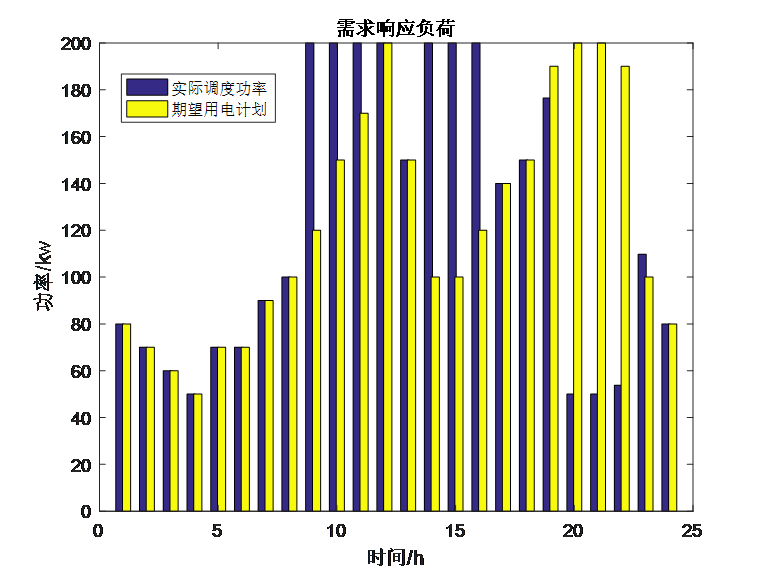

从运行结果可以看出,使用KKT条件可以正常求出最优解,但由于引入了非常多的拉格朗日乘子和相应的0-1变量,对于初始的约束形式手动写KKT条件非常麻烦,一旦出错也很难发现问题在哪。
3.2 将两阶段鲁棒优化问题写成矩阵形式
对于约束条件比较复杂的两阶段鲁棒优化问题,先把目标函数和约束条件写成紧凑的矩阵形式再使用KKT条件或对偶变换求解会方便很多。文献[1]中将优化问题写成了紧凑的矩阵形式,但存在一定问题,我在此重新梳理一遍。
首先,将优化问题写成紧凑的矩阵形式(等式约束都改写成不等式形式,例如x=0可以写成x≥0,-x≥0):
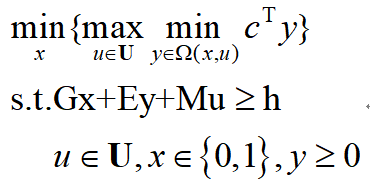
其中,第一阶段决策变量x是一个48维的列向量:
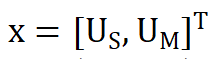
第二阶段决策变量y是一个192维的列向量:
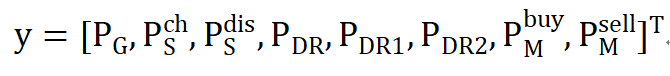
c和y的维度一样,但c是一个192维的常数列向量:
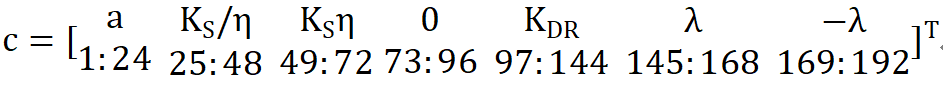
那么如何确定矩阵G,矩阵E,矩阵M,向量h的取值呢?之前的博客中我采用了手动推导的方式(微电网两阶段鲁棒优化经济调度方法matlab代码)。
这次我来教大家使用Yalmip工具箱中的函数depends、getbase、getbasematrix、see写出约束矩阵取值的方法,函数的语法可以参考官方文档。
下面是一个简单的线性规划问题:

我用这个例子来帮助大家体会depends、getbase、getbasematrix、see等函数的用法,代码如下:
clc
clear
close all
warning off
yalmip('clear')
%% 决策变量
sdpvar x1 x2
%% 目标函数
obj = x1 + 2*x2;
z = [-2*x1 + 3*x2 - 12 ;
x1 + x2 - 14;
-3*x1 + x2 + 3;
3*x1 + x2 - 30];
x1_index = depends(x1)
x2_index = depends(x2)
M1 = full(getbase(z))
M2 = full(getbasematrix(z,depends(x1)))
M3 = full(getbasematrix(z,depends(x2)))
see(z)
运行结果如下:
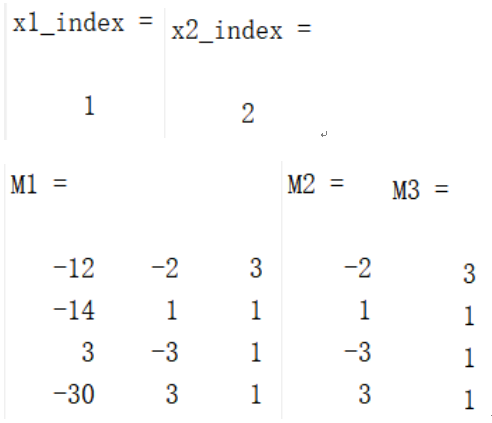
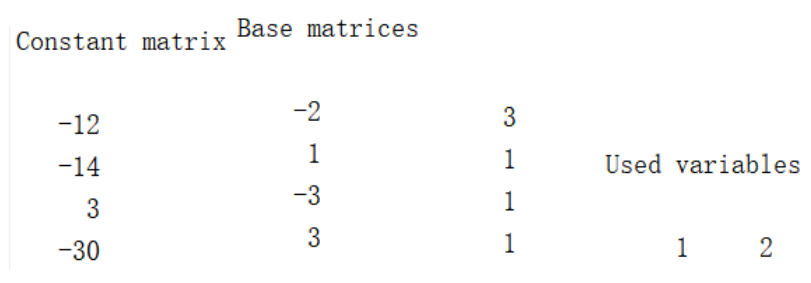
观察可知,depends函数返回的是变量在Yalmip工具箱中的编号,getbase函数以稀疏矩阵的形式返回sdpvar变量中的常数项系数以及变量系数,getbasematrix函数以稀疏矩阵的形式返回sdpvar变量中指定编号的变量系数,see函数直接在命令行输出sdpvar变量中的常数项、变量系数以及用到的变量编号。
假设我们想把上面的优化问题写成紧凑的矩阵形式:
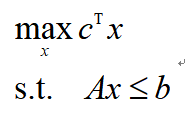
求矩阵A、b、c,然后使用矩阵形式求解优化问题的代码如下:
clc
clear
close all
warning off
yalmip('clear')
%% 决策变量
sdpvar x1 x2
%% 求系数矩阵
obj0 = x1 + 2*x2;
z = [-2*x1 + 3*x2 - 12 ;
x1 + x2 - 14;
-3*x1 + x2 + 3;
3*x1 + x2 - 30];
M1 = full(getbase(z));
M2 = full(getbase(obj0));
index = depends([x1 x2]);
A = M1(:,index + 1);
b = -M1(:,1);
c = M2(index + 1)';
%% 矩阵形式的目标函数
x = [x1;x2];
obj = c'*x;
C = [A*x <= b , x >= 0];
%% 求解优化问题
ops = sdpsettings('verbose', 3, 'solver', 'gurobi');
sol = optimize(C , -obj ,ops);
%% 判断求解是否成功
if sol.problem == 0
disp('求解成功!!!');
x = value(x)
else
disp(['求解失败,原因为',sol.info]);
end
运行结果如下:
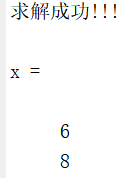
采用相同的方法,将文献[1]所提确定性优化问题改写成矩阵形式求解的代码在压缩包中的Problem2文件夹中,运行Problem2_matrix.m文件即可得到结果。

3.3 矩阵形式的C&CG算法与KKT条件求解
原始子问题为:
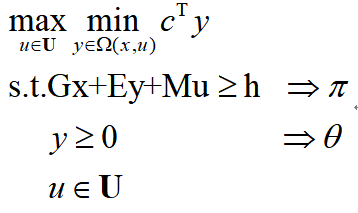
内层优化中变量x和不确定变量u都可以看作常数,其拉格朗日函数可以写作:
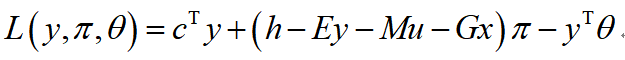
其中,π和θ都是拉格朗日乘子。根据拉格朗日函数进一步写出KKT条件:
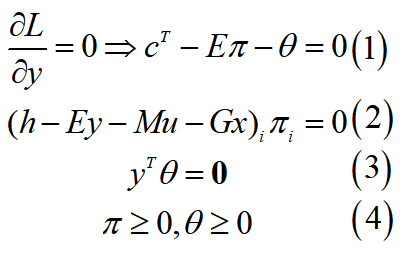
这就是初始的KKT条件,可以进一步化简。首先根据式(1)和(4)可以得到:
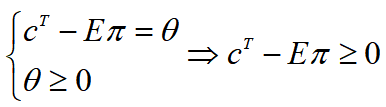
然后,根据式(1)和(3)可以得到:
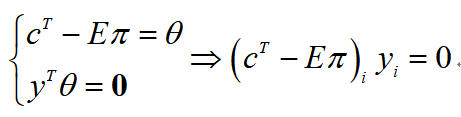
经过这样处理,就可以消去变量θ,减少决策变量的数目,得到:
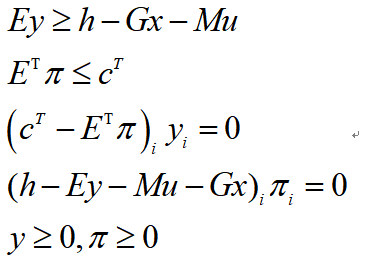
其中包含两项互补松弛条件,可以通过引入0-1变量,使用大M法转换为线性约束:
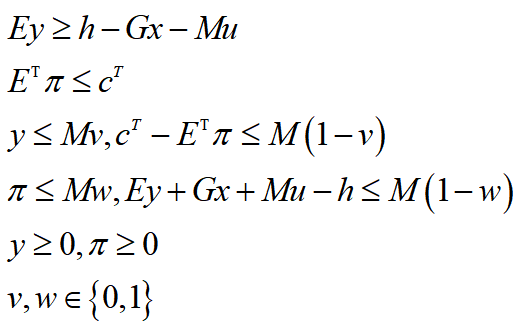
将KKT条件添加到子问题的外层优化中,子问题便转为:
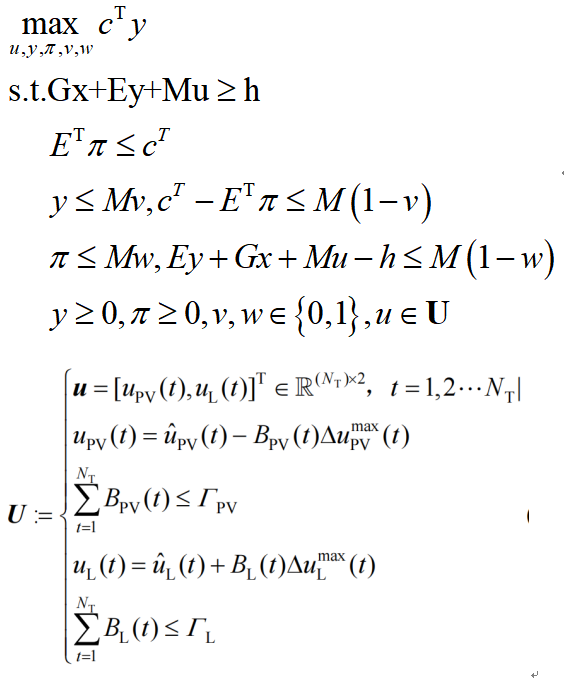
子问题变成了一个混合整数线性规划,可以采用求解器有效地进行求解。
再复习一下,我们把文献[2]中所提两阶段鲁棒优化分解成一个主问题MP2_KKT和一个子问题SP2_KKT:
主问题MP2_KKT:
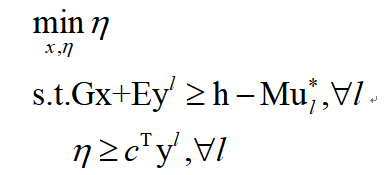

子问题SP2_KKT:
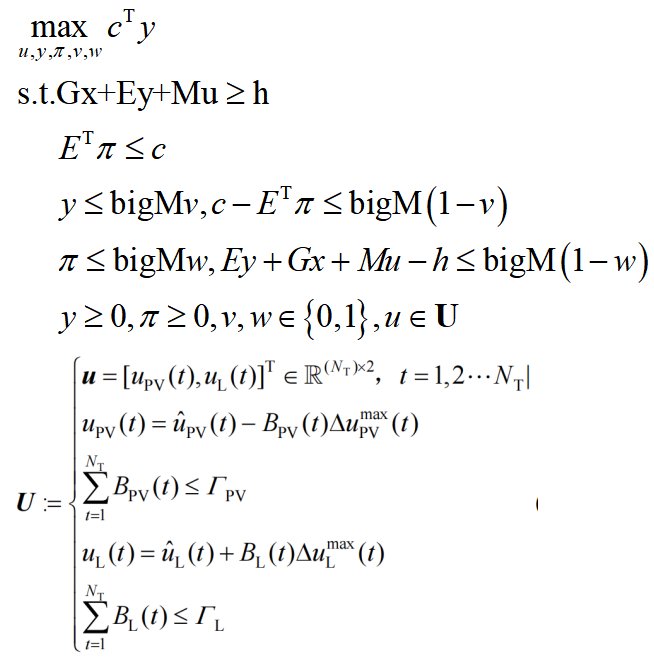


使用KKT条件+C&CG算法求解该两阶段鲁棒优化问题的代码在压缩包中的Problem2文件夹中,运行Problem2_KKT.m文件即可得到结果。
3.4 矩阵形式的C&CG算法与对偶变换求解
原始子问题为:
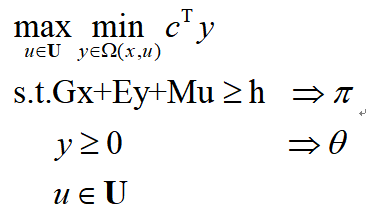
其内层优化min问题的对偶问题可以写做:
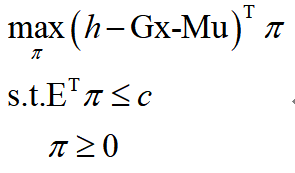
将其与外层max问题合并得到:

该问题的目标函数中包含的非线性项,可以进行线性化,也可以直接使用求解器进行求解。为了方便起见,我直接使用了求解器进行求解。但是由于问题规模比较大,求解时间会比较长(大概要3小时左右才能得到最优解)。
首先,将不确定变量u写成:
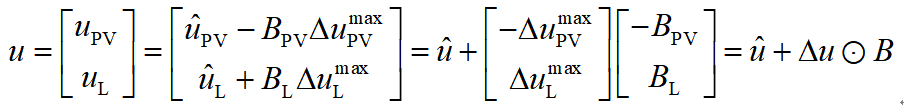
式中,符号表示矩阵的Hadamard乘积(哈达玛积 Hadamard Product - 知乎),即对应元素相乘,对应于matlab中的“.*”符号。在此基础上,可以对原优化问题的目标函数进行化简:
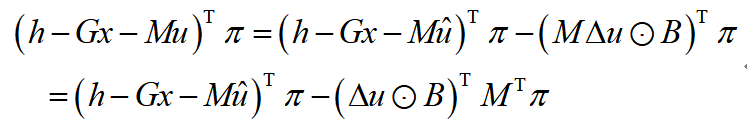
两阶段鲁棒优化问题可以分为主问题和子问题:
对偶变换版本主问题MP2_dual:
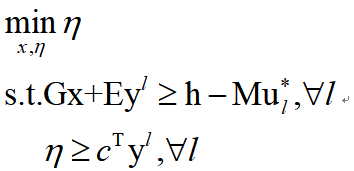
对偶变换版本子问题SP2_dual:
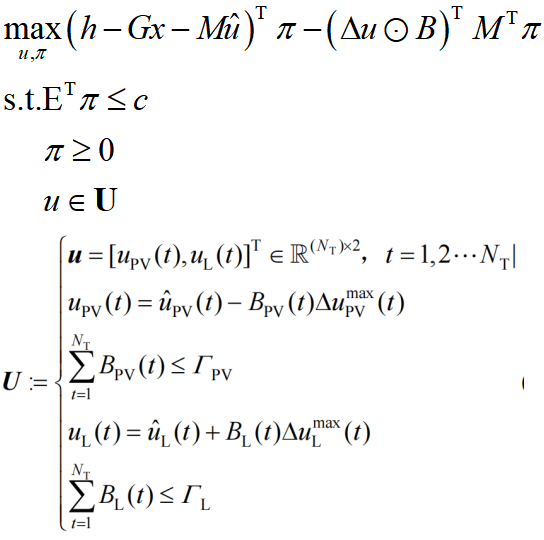
使用C&CG算法与对偶变换求解两阶段鲁棒优化的步骤概括如下:


使用对偶变换+C&CG算法求解该两阶段鲁棒优化问题的代码在压缩包中的Problem2文件夹中,运行Problem2_dual.m文件即可得到结果。
参考文献:
[1]Zeng B, Zhao L. Solving two-stage robust optimization problems using a column-and-constraint generation method[J]. Operations Research Letters, 2013, 41(5): 457-461.
[2]刘一欣,郭力,王成山.微电网两阶段鲁棒优化经济调度方法[J].中国电机工程学报,2018,38(14):4013-4022+4307.
PS:
完整资料付费后可以获取。
参考文献:
[1]Zeng B, Zhao L. Solving two-stage robust optimization problems using a column-and-constraint generation method[J]. Operations Research Letters, 2013, 41(5): 457-461.
[2]刘一欣,郭力,王成山.微电网两阶段鲁棒优化经济调度方法[J].中国电机工程学报,2018,38(14):4013-4022+4307.