基于Python控制台的贪心算法的快递物流路径优化

作品简介

以下是一个适合大一、大二大数据分析专业学生的 快递物流路径优化课程设计程序，结合模拟数据、优化算法和可视化，帮助学生了解物流路径优化问题的基本概念和解决方法。

程序功能简介

  1. 数据生成：
  • 模拟多个配送点的经纬度和包裹需求。
  • 生成配送中心位置。
  1. 路径优化：
  • 使用距离矩阵和简单的贪心算法进行路径优化。
  • 计算总配送距离。
  1. 结果可视化：
  • 绘制配送中心和配送点的路径图，直观展示优化结果。

部分代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.spatial.distance import cdist

# 1. 生成模拟快递点和配送中心数据
def generate_delivery_data(num_points=10):
    np.random.seed(42)  # 固定随机种子，保证结果一致
    # 配送点的经纬度
    delivery_points = pd.DataFrame({
        "配送点": [f"Point_{i+1}" for i in range(num_points)],
        "经度": np.random.uniform(100.0, 110.0, num_points),  # 模拟经度范围
        "纬度": np.random.uniform(30.0, 40.0, num_points),   # 模拟纬度范围
        "包裹需求": np.random.randint(1, 10, num_points)     # 每个点的包裹需求
    })
    # 配送中心位置
    delivery_center = pd.DataFrame({
        "名称": ["Center"],
        "经度": [105.0],  # 固定配送中心经度
        "纬度": [35.0],   # 固定配送中心纬度
    })
    return delivery_points, delivery_center

# 2. 路径优化（贪心算法）
def optimize_delivery_route(delivery_points, delivery_center):
    # 将配送点和中心的坐标转换为数组
    points_coords = delivery_points[["经度", "纬度"]].values
    center_coords = delivery_center[["经度", "纬度"]].values

程序功能解析

1. 数据生成

  • 配送点数据：
  • 随机生成 10 个配送点的经纬度。
  • 每个配送点包含 包裹需求 数据（1-10 个包裹）。
  • 配送中心数据：
  • 固定配送中心的经纬度位置。
  • 默认设置在 (105.0, 35.0)。

2. 路径优化

  • 贪心算法：
  • 计算配送点到配送中心的距离。
  • 按照距离排序，优先选择最近的配送点。
  • 优化目标：
  • 通过排序的方式生成一个简单的路径优化方案。
  • 可以扩展为更复杂的算法（如动态规划或 TSP）。

3. 数据可视化

  • 可视化内容：
  • 配送点和配送中心在地图上的位置。
  • 配送路径的连线（使用虚线标记优化路径）。
  • 包括配送点的标注和中心位置的标注。
  • 工具：
  • 使用 Matplotlib 绘制路径和点。
  • 动态生成路径线段，展示路线连接效果。

运行结果示例

1. 优化后的配送路径

优化后的配送路径：
     配送点       距离  包裹需求
0  Point_8  0.290334     6
1  Point_7  0.564927     2
2  Point_3  0.711922     4
3  Point_10 0.881355     1
4  Point_6  1.110055     7
...

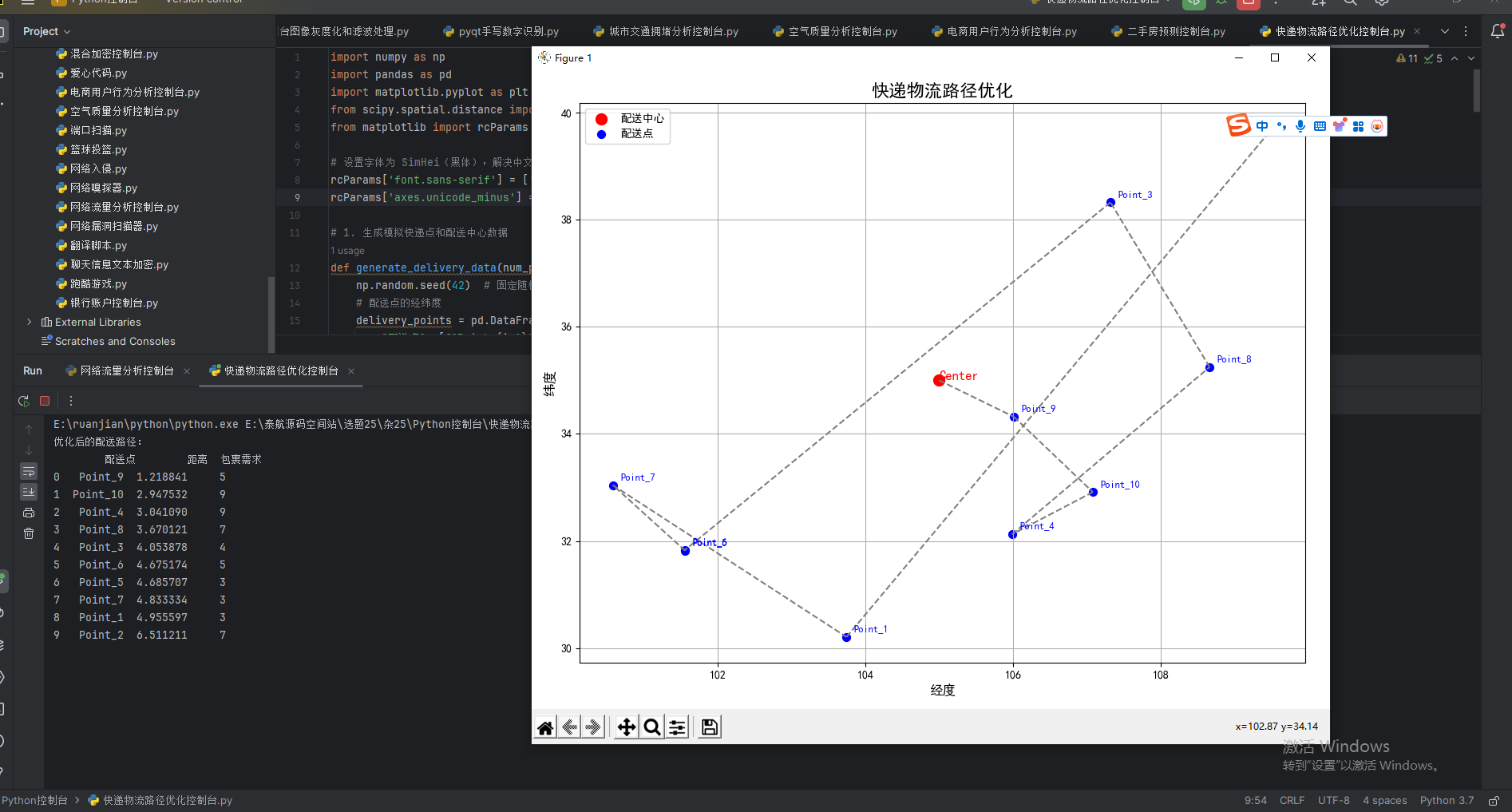
2. 可视化图表

  1. 配送点和配送中心：
  • 红点代表配送中心。
  • 蓝点代表配送点。
  • 每个点旁边标注了配送点名称。
  1. 优化路径：
  • 虚线表示配送中心到配送点的路线。
  • 按距离依次连接配送点。

课程设计亮点

  1. 贴近实际场景：
  • 结合快递物流场景，模拟真实的配送路径优化问题。
  • 涉及经纬度、距离计算和路径规划。
  1. 基础算法应用：
  • 使用简单的贪心算法作为优化方法，便于理解和扩展。
  • 可进一步扩展为复杂算法（如最短路径或动态规划）。
  1. 可视化增强理解：
  • 绘制配送路径图，直观展示优化效果。
  • 配送点标注和路径线段清晰可见。
  1. 可扩展性：
  • 增加包裹权重、时间窗口等约束条件。
  • 使用高级优化算法（如遗传算法、TSP 求解）改进路径规划。

扩展任务建议

  1. 高级算法扩展：
  • 引入动态规划或蚁群算法解决路径优化问题。
  1. 约束条件优化：
  • 添加配送时间窗口或最大车辆负载限制。
  1. 真实数据分析：
  • 使用实际的地理数据和交通数据进行路径优化。
  1. 多中心优化：
  • 模拟多个配送中心的场景，分配配送任务。

该程序既能帮助学生理解路径优化的基础知识，又能激发学生探索更复杂算法的兴趣，非常适合作为课程设计作业！


创作时间：