一、求解思路

LSTM（Long Short Term Memory）是具有记忆长短期信息的能力的神经网络，传统的训练方式采用梯度下降。然而，梯度下降方法容易陷入局部最优，群智能优化算法具有较强的全局搜索能力。本文采用麻雀搜索算法（SSA）直接优化LSTM的权值和阈值，提高LSTM的求解精度。

本文采用的数据集如下：data=3*sin(0:0.02:30);%数据集

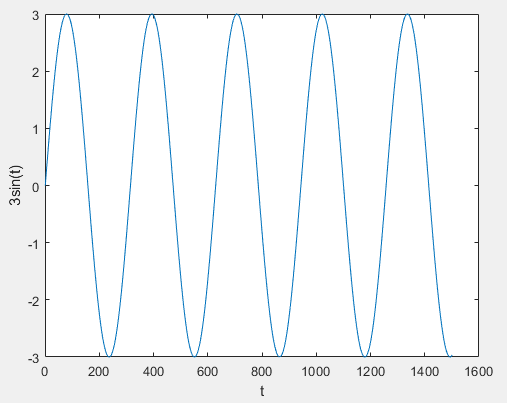
训练集和测试集各占数据集的70%和30%。SSA优化LSTM的目标函数为训练集上真实值和预测值的均方误差（MSE）。

二、实验结果

2.1部分代码

Dim=sum(sum(K(:,1).*K(:,2)));%维度
lb=-5;%下界
ub=5;%上界
fobj=@Fun;%计算训练集上的函数值（真实值与预测值的均方误差MSE）
SearchAgents_no=50; % 种群大小（可以修改）
Max_iteration=100; % 最大迭代次数（可以修改）
[fMin,bestX,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,Dim,fobj);  %SSA优化LSTM的权值阈值 bestX是最优权值阈值
o=TestFun(bestX);%在测试集上预测
o1=TrainFun(bestX);%在训练集上预测
save bestX bestX %保留SSA优化LSTM得到的最优参数
save SSA_curve SSA_curve %保留
%% 画出SSA优化LSTM的均方误差随迭代次数的图
figure
semilogy(SSA_curve,'Color','g')
xlabel('Iteration');
ylabel('MSE');
legend('SSA')
%%
display(['The best solution obtained by SSA is : ', num2str(bestX)]);
display(['The best optimal value of the objective funciton found by SSA is : ', num2str(fMin)]);%fMin越小说明SSA优LSTM效果越好

2.2求解结果：

训练集上MSE随迭代次数变化的曲线图：

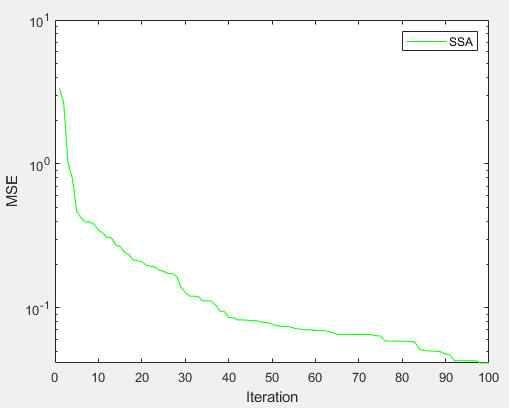
训练集上真实值和预测值对比图：

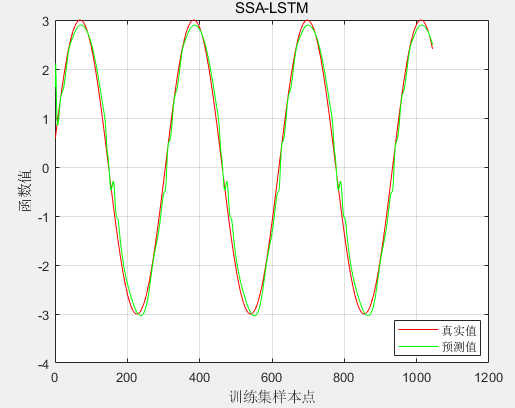
训练集上真实值和预测值绝对误差（MAE）：

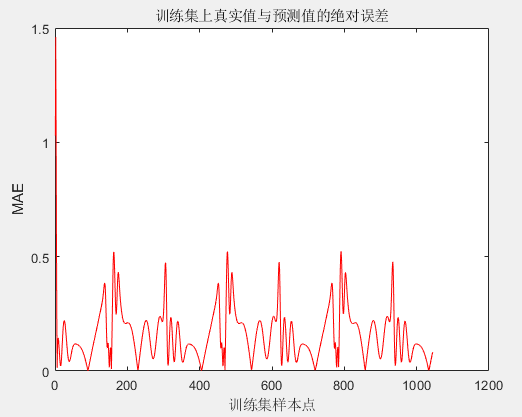
测试集上真实值和预测值对比图：

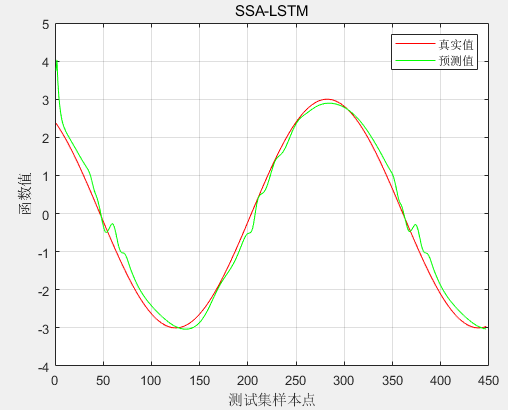
测试集上真实值和预测值绝对误差（MAE）：

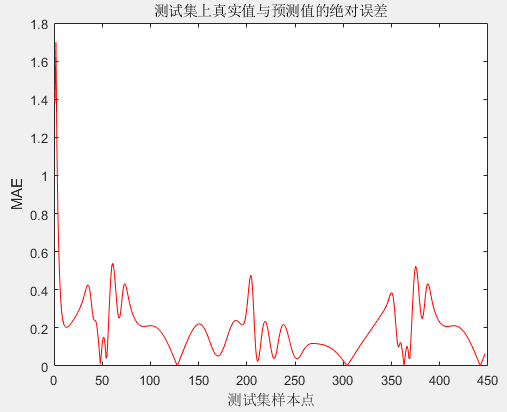
由此可见，SSA优化LSTM不管在训练集上还是测试集上均能达到理想结果，预测值与真实值十分接近。

三、参考代码：

文件夹内包含所有代码，可以直接运行，LSTM隐藏层的神经元个数可自行修改，包含使用说明。