一、求解思路

求解定义在[0,1]x[0,1]的如下偏微分方程

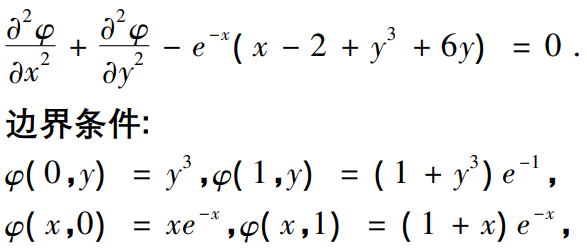
通过麻雀搜索算法（SSA）优化BP神经网络的权值阈值，目标函数为上述偏微分方程的真实目标值和BP神经网络的输出预测值的均方误差（MSE）。

二、求解结果

2.1部分代码：

close all
clear
clc
global inputnum hiddennum outputnum TrainNum 
inputnum=2;%神经网络输入层神经元个数（输入样本维度）
hiddennum=10;%神经网络隐藏层神经元个数（可以自己修改） 
outputnum=1;%神经网络输出层神经元个数（输出样本维度）
TrainNum=1156;%训练集数目 
%% 麻雀搜索算法SSA优化BP神经网络求解偏微分方程，目标函数是均方误差MSE
SearchAgents_no=50; %种群大小（可以修改）
Function_name='F1'; 
Max_iteration=500; %最大迭代次数（可以修改）
[lb,ub,dim,fobj]=fun_info(Function_name);% 在fun_info.m中可以查看上下限及目标函数
[fMin,bestX,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);  %SSA优化BP神经网络的权值阈值 bestX是最优权值阈值
save bestX bestX %保留SSA优化BP神经网络得到的最优权值阈值
%%
TrainPre(bestX) %训练集预测
%% 画出SSA优化BP神经网络的均方误差随迭代次数的图
figure
semilogy(SSA_curve,'Color','g')
title('Objective space')
xlabel('Iteration');
ylabel('MSE');
grid on
box on
legend('SSA')
%%
display(['The best solution obtained by SSA is : ', num2str(bestX)]);
display(['The best optimal value of the objective funciton found by SSA is : ', num2str(fMin)]);%fMin越小说明SSA优化BP神经网络效果越好

2.2结果如下：

MSE随迭代次数变化图：

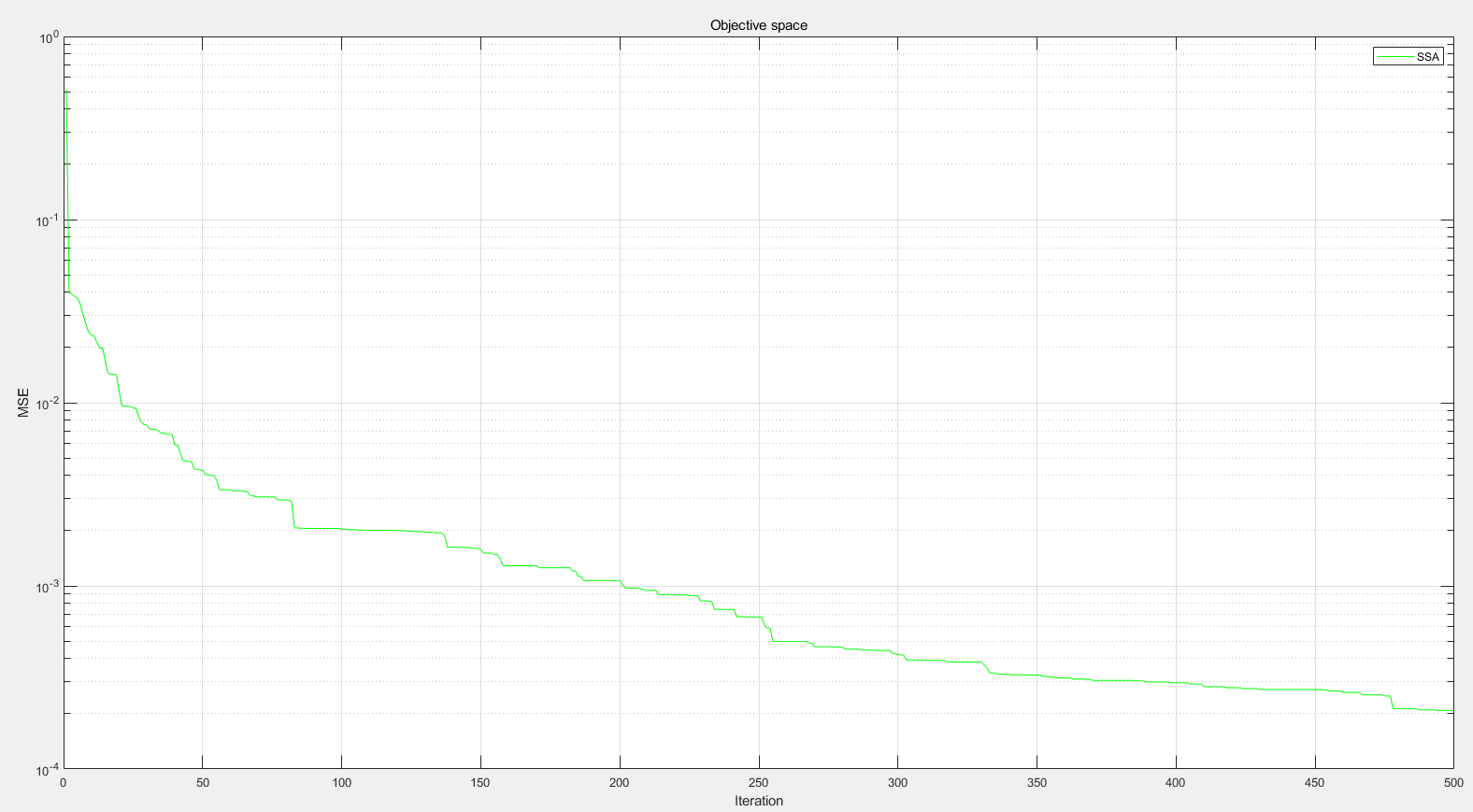
真实值与预测值图：

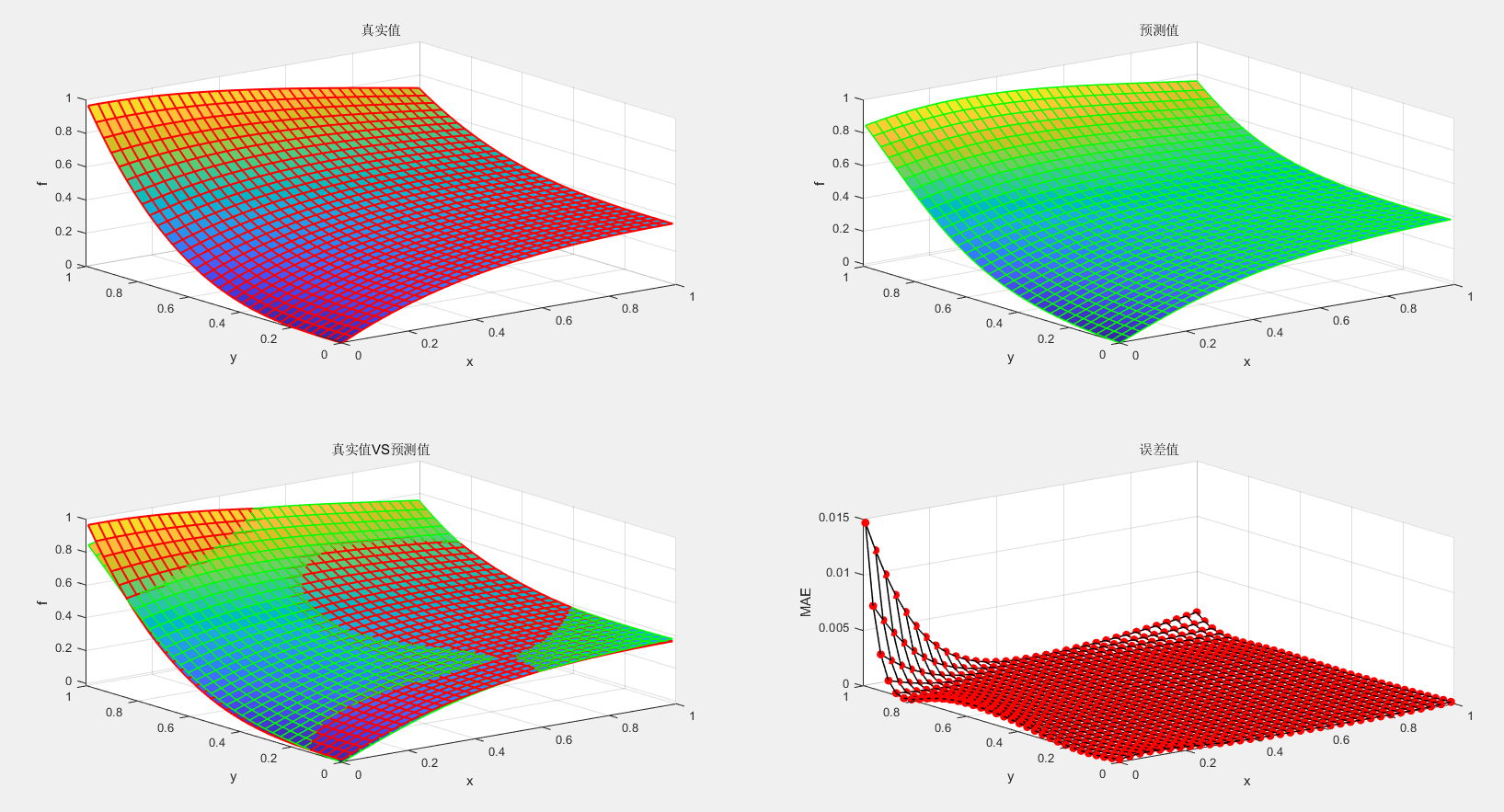
可以看出SSA优化BP神经网络用于求解偏微分方程十分有效，真实值和预测值非常接近，效果显著。

三、参考代码

文件夹内包含所有代码，含有使用说明，点击main.m即可运行。