一、算法简介

鳄鱼狩猎策略优化算法（crocodiles hunting strategy optimization algorithm，CHS）由Alireza Balavand于2021年提出，该算法的主要灵感来自鳄鱼狩猎策略。

二、算法原理

鳄鱼狩猎策略优化算法模拟了鳄鱼的捕食行为，将鳄鱼种群分为追逐者和伏击者，分别对应捕食行为中的追逐猎物和攻击猎物两个阶段。

2.1 追逐猎物

追逐者为种群中适应度值较优的前一半个体，伏击者为种群中剩下的个体，各占种群大小的一半。

在追逐猎物阶段，如果追逐者靠近猎物，则攻击由追逐者完成，否则，通过靠近猎物的随机接近，通过以下模型模拟该过程。

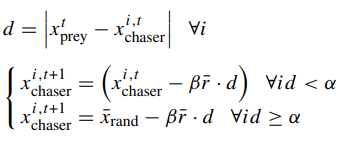
2.2 攻击猎物

在攻击猎物阶段，每个伏击者要么以旋转运动在猎物周围运动，要么根据所有追逐者、伏击者和猎物的姿势平均值来更新自己的位置，通过以下模型模拟该过程。

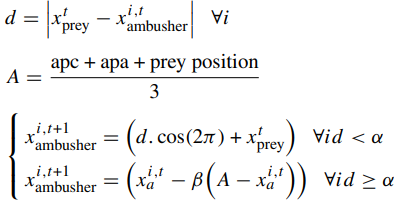
三、算法流程

四、多目鳄鱼狩猎策略优化算法MOCHS

4.1函数测试

将鳄鱼狩猎策略优化算法的优良策略与多目标优化思想结合，形成多目鳄鱼狩猎策略优化算法（MOCHS），为了验证所提的MOCHS的有效性，将其在46个多目标测试函数（ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3）上实验。

ZDT1：

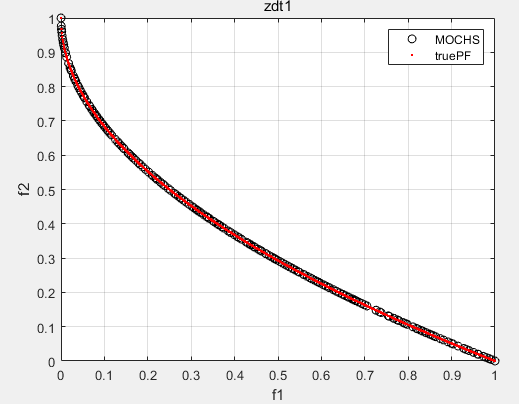
ZDT2：

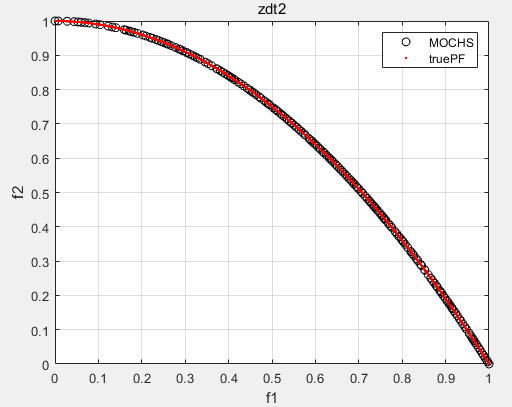
ZDT3：

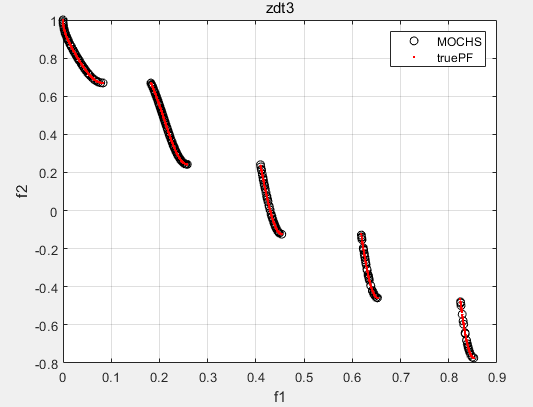
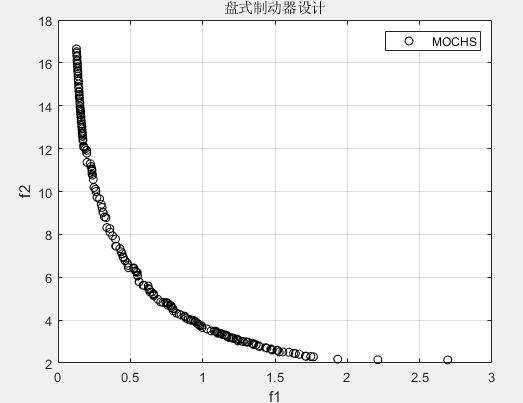
4.2 工程应用

设计优化，特别是结构设计，在工程当中有着广泛 的应用。盘式制动器设计是一个广为人知的多目标 工程设计问题。该问题有4个设计变量：圆盘外半径 R 和内半径r，接合力F和摩擦表面数目s。

目标是最小化 制动器质量 f1( x )和制动时间 f2( x)。 该设计的约束包括 半径之间的最小距离、制动器的最大长度、压力、温度和 扭矩的限制，分别用g1( x )、g2( x )、g3( x )、g4( x )和g5( x )表示 。 问题描述如下：

最小化目标：

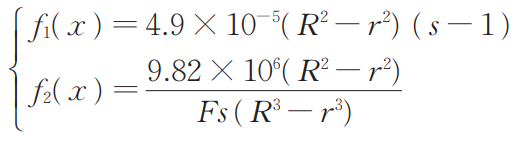
约束条件：

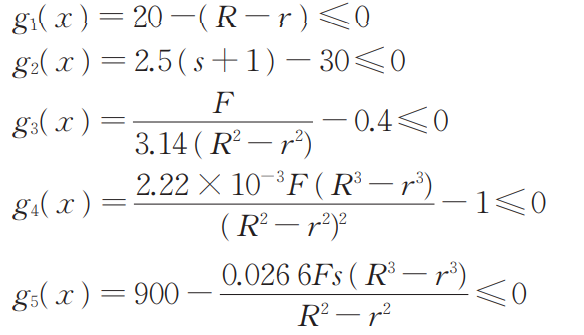
其 中 ，55 ≤ r ≤ 80,75 ≤ R ≤ 110,1 000 ≤ F ≤ 3 000,2≤ s ≤ 20 

4.3指标评价

（1）迭代距离（Generational Distance，GD）：衡量真实 PF 上与近似解集之间的间隔距离。需要预先获得一组在真 实 PF 上均匀采样的解集。GD 值越小，表示 S 具有越好的收敛性，越能逼近整个 PF。

（2）反向迭代距离 (Inverted Generational Distance，IGD） 衡量的是真实 PF 的个体到算法求得的近似解集之间最小 距离的平均值，因此计算 IGD 需要预先获得一组在真实 PF 上均匀采样的解集。IGD 值越小，表示 具有越好的收敛与多样性能，越能逼近整个 PF。

（3）超体积指标( Hypervolume，HV）指给定一组预先设置 分布在目标空间的参考点 r 与一组由算法 得到的 PF 近似解集 S ，满足 r 被 S 中所有解支配。HV 衡 量的是以 r * 为边界、被 S 支配目标空间的体积大小。HV 值越大，表示 S 越 近似于整个 PF。

（4）空间评价方法(Spacing Metric，SP）用于衡量每个解到其他相邻解之间最小距离的标准差，SP值越小，说明解集越均匀。

4.4 参考文献

[1]温泽宇,谢珺,谢刚,续欣莹.基于新型拥挤度距离的多目标麻雀搜索算法[J].计算机工程与应用,2021,57(22)

[2]胡涵,李振宇.多目标进化算法性能评价指标综述[J].软件导刊,2019,18(09):1-4.

五、源文件

源文件夹包含MOCHS所有代码（含46个多目标测试函数、1个工程应用、4种评价指标）。代码可直接运行，支持二次开发，MOCHS效果非常棒，算法新颖，求解速度快，大力推荐。