声明：文章是从本人公众号中复制而来（如图片无法显示可前往本人公众号或CSDN搜索对应标题查看）。想最新最快了解各类智能优化算法及其改进的朋友，可关注我的公众号：强盛机器学习，不定期会有很多免费代码分享~

之前给大家带来过很多机器学习预测的代码，比如 LSTM、GRU、CNN等等，但这些模型已经快被彻底用烂了，比如中高频预测、机械故障诊断、能源时序等等，审稿人已经见得太多。

因此，今天给大家介绍一个新颖且非常有潜力的模型——KAN（Kolmogorov-Arnold Networks），这个模型2024年刚刚在NeurIPS 2024这个顶级会议上发表，随后又被IEEE TNNLS、Pattern Recognition等顶级期刊重点引用，目前，知网和WOS上直接将其用于预测任务的还非常少，也更容易受到审稿人和期刊的欢迎。

可惜，网上绝大部分开源实现都是 Python，但是Python需要配置环境，且不同版本差异较大，难以直接在电脑上运行，非常不适合新手小白。同时，部分Python代码非常混乱，使用的库也不统一，真假难辨。

因此，今天给小伙伴带来一期利用Matlab实现KAN神经网络预测的代码。代码非常清晰易懂，也跟以前的形式一样，直接Excel替换数据即可！无需更改代码！

01

案例数据

本期采用的案例数据依旧是经典的回归预测数据集，是为了方便大家替换自己的数据集，各个变量采用特征1、特征2…表示，无实际含义，最后一列即为输出。

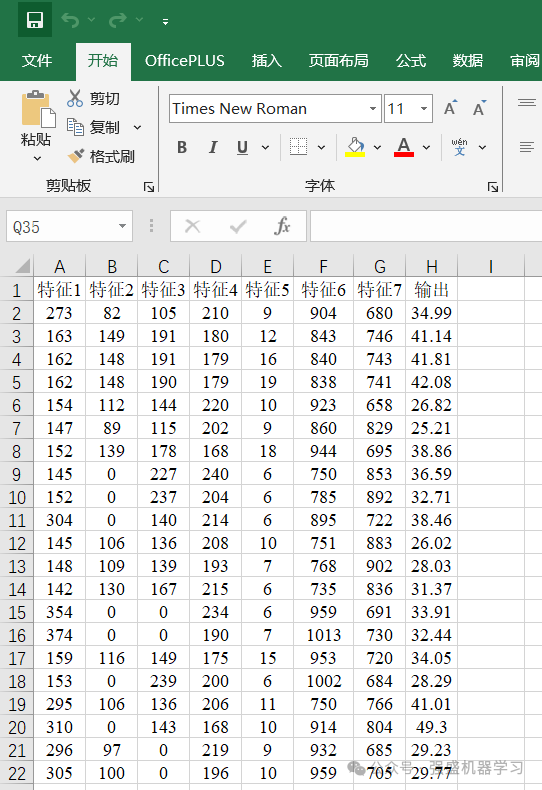
更换自己的数据时，只需最后一列放想要预测的列，其余列放特征即可（特征数量不限），无需更改代码，非常方便！

02

原理简介

传统 的 MLP 使用固定的激活函数（如 ReLU 、 Sigmoid 等）来处理数据，而 KAN 的创新之处在于采用了可学习的激活函数——样条函数（ B-spline ）。它能根据数据的变化自动调整形状，更精确地捕捉复杂的非线性关系，使网络在保持灵活性的同时，能以较少的参数实现对复杂网络结构的拟合。

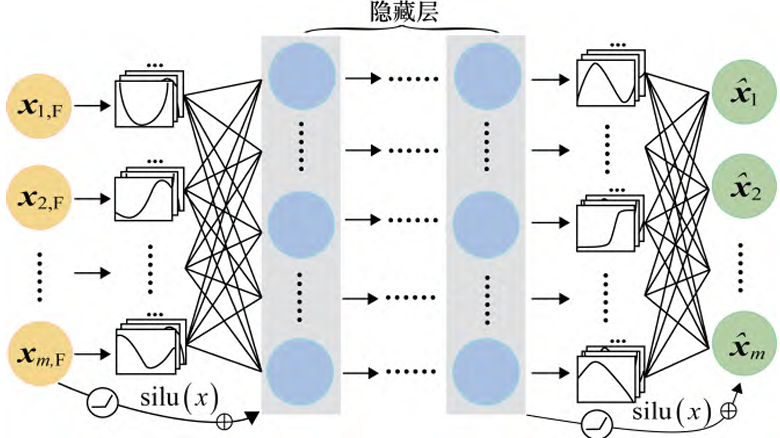
KAN 的公式表达基于 Kolmogorov-Arnold 表示定理展开。以一个简单的形式为例，一个多元函数 f(x1,x2, ⋅⋅⋅ ,xn) 可以通过下式表示：

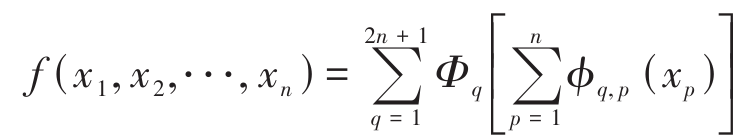
式中： x1,x2, ⋅⋅⋅ ,xn 为输入特征； Φq 和 ϕq,p 均为单变量连续函数， Φq 为外层函数， ϕq,p 为内层函数。在训练过程中， KAN 通过 Φq,ϕq,p 构建输入特征与共享单车需求量之间的复杂映射关系。激活函数 ϕ(x) 表达式为：

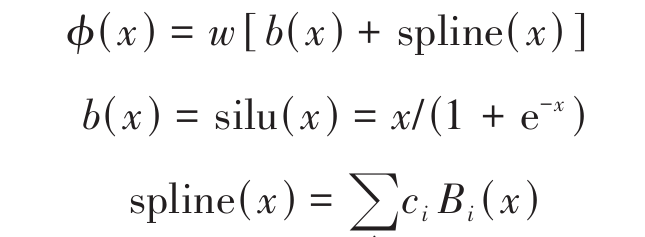
式中： w 和 ci 均为可学习参数； b(x) 为偏置激活函数，在 KAN 中该函数被初始化为 silu 激活函数； spline(x) 为一组一维函数组合； Bi(x) 为预先定义的 Base- 样条基函数。在训练过程中样条参数 ci 持续优化，以调整样条形状，使得能够准确描述特征与需求量之间的非线性关系，从而拟合训练数据。

03

结果展示

用上文提到的数据集进行测试，步骤如下：

Step 1  读取 Excel数据

Step 2  设定隐层宽度nH 、样条结点 nKnots 【也可以直接用默认参数】

Step 3  运 行 main.m —— 自动完成训练、预测、可视化、指标显示

Step 4  查看输出结果（出的图非常多！）：

🔹 训练/测试对比图

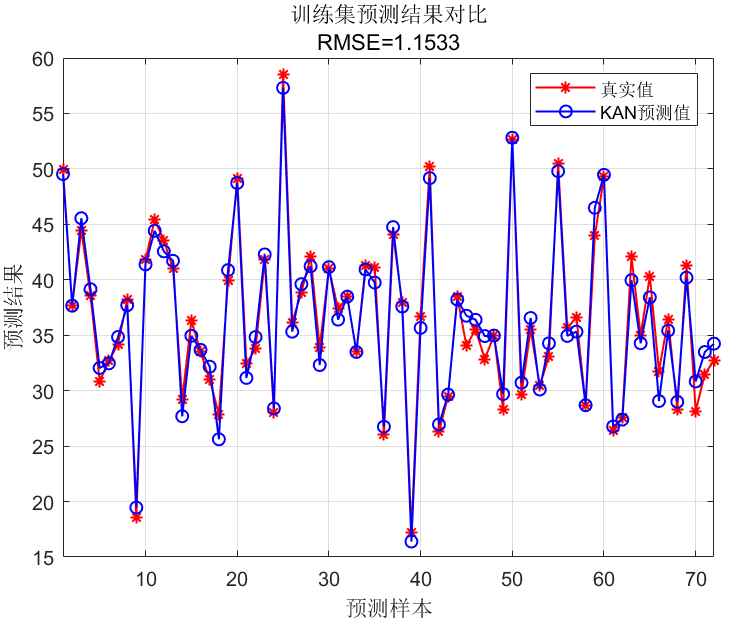
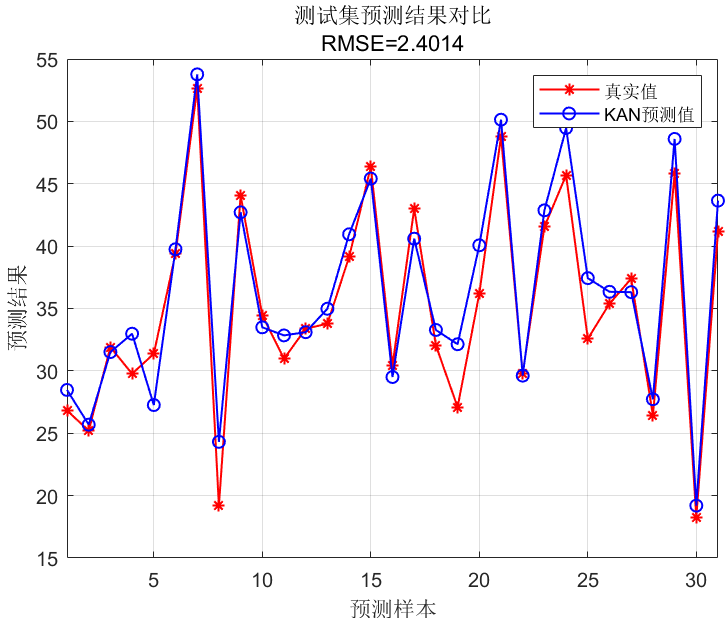
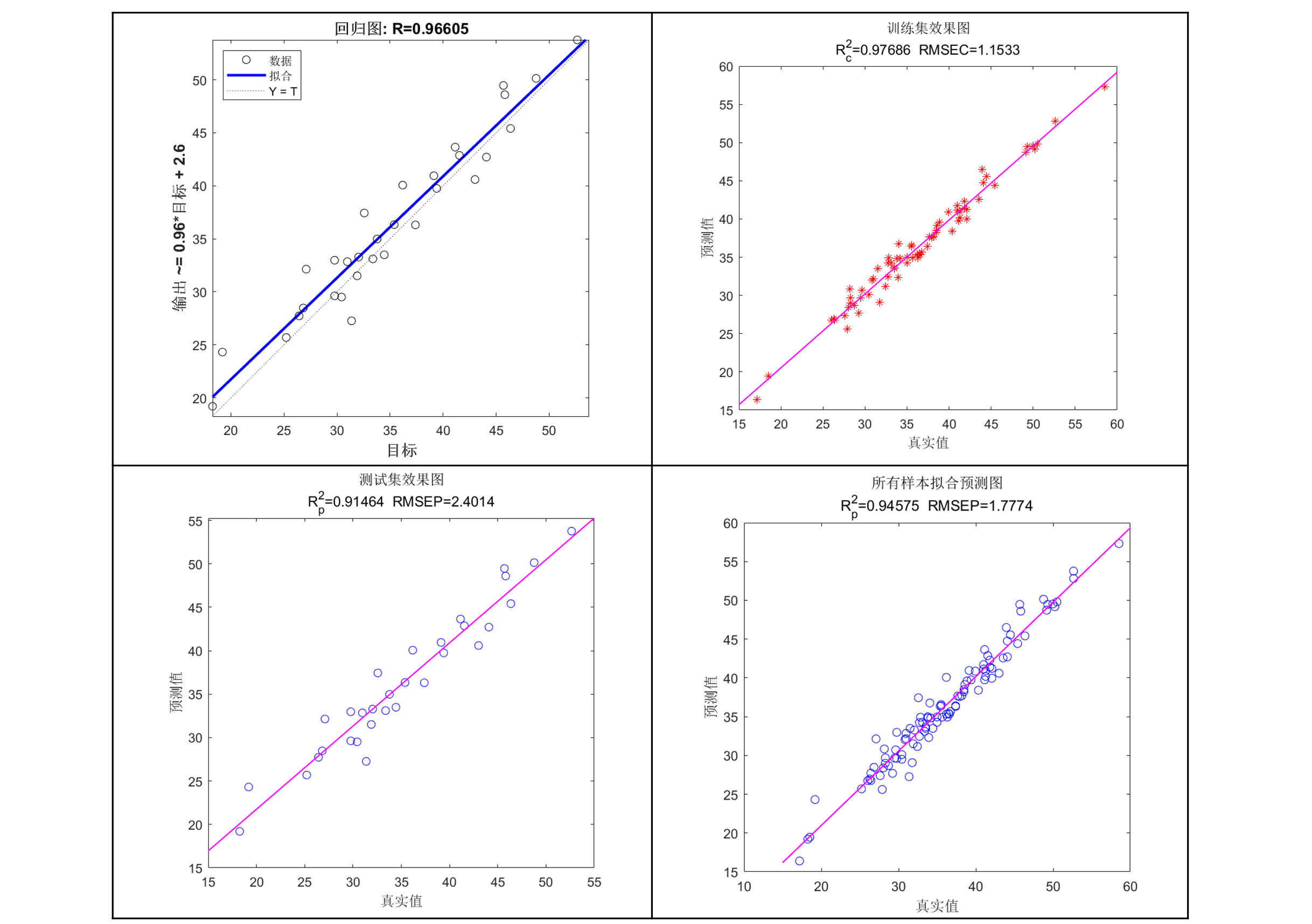
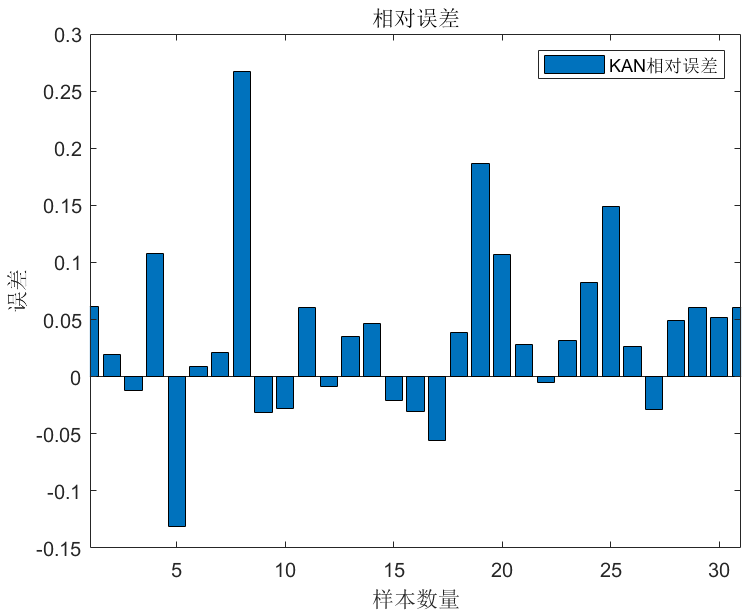
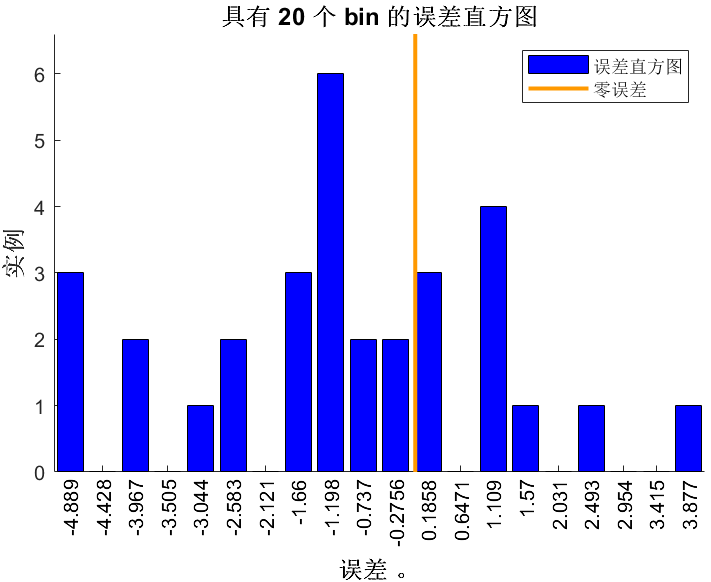
🔹 四张回归图 & 两张误差直方图

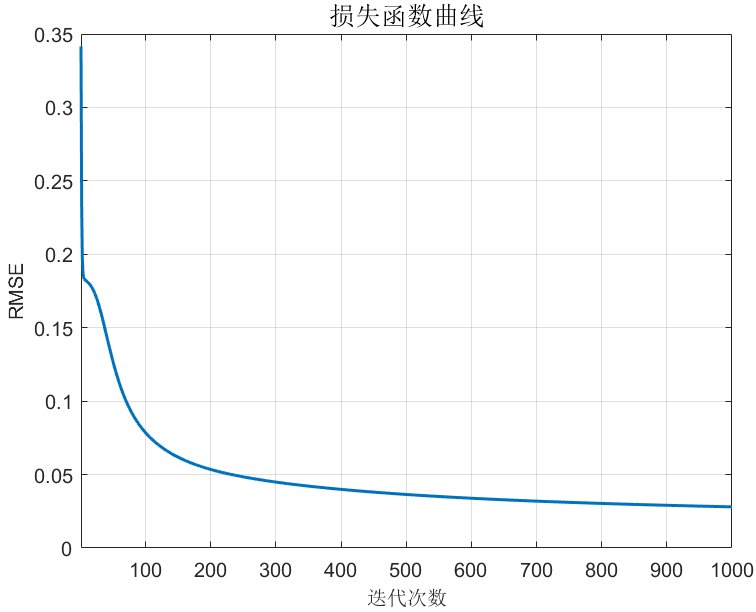
🔹损失函数曲线图

🔹输出指标 （RMSE、MAE、R²、MAPE）

  Epoch: 0993 of 1000
  Epoch: 0994 of 1000
  Epoch: 0995 of 1000
  Epoch: 0996 of 1000
  Epoch: 0997 of 1000
  Epoch: 0998 of 1000
  Epoch: 0999 of 1000
  Epoch: 1000 of 1000
训练集数据的R2为：0.97146
测试集数据的R2为：0.92363
训练集数据的MAE为：0.98374
测试集数据的MAE为：1.8758
训练集数据的RMSE为：1.2443
测试集数据的RMSE为：2.3524
训练集数据的MAPE为：0.029004
测试集数据的MAPE为：0.054626

可以看到，我们的KAN模型在该回归数据集上的预测精度还是不错的，迭代1000次后R2就达到了0.92多，当然，由于时间关系我这边只设置了运行1000次，大家运行次数更多说不定效果会更好~

当然，不同数据集效果不同，大家可按照上文数据替换方法将自己的数据集替换到程序内查看效果~

我们文件夹内也非常清晰，没有什么乱七八糟的文件！您需要运行的文件只有main脚本一个！

以上所有图片，替换Excel后均可一键运行main生成，Matlab无需配置环境！比Python什么方便多了！非常适合新手小白！

04

部分代码展示

%%  添加路径
addpath('KAN\')
%%  导入数据
res = xlsread('数据集.xlsx');
%%  数据分析
num_size = 0.7;                              % 训练集占数据集比例
outdim = 1;                                  % 最后一列为输出
num_samples = size(res, 1);                  % 样本个数
res = res(randperm(num_samples), :);         % 打乱数据集（不希望打乱时，注释该行）
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度
%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';
%%  参数设置
nH  = 15;                               % 隐层宽度
nKnots = 5;                             % 每条边样条结点数
Nrun = 1000;                            % 训练遍历次数
alp = 1e-2;                             % 学习率