一、最优化问题现状

很多科学、经济、工程中的问题都可以建模为全局优化问题来解决，比如求解满足一定条件的最小的开销、最短的路线、最优的调度序列等等。对于部分待求解的问题，问题的详细信息是已知的，并且容易建模，对于这类有详细表达式信息的问题我们称为白盒问题。但是有些问题较为复杂，比如问题是非凸的，不可微的，或者存在数目巨大的局部最优解，从而使得很多优化算法无法高效的进行求解。还有一部分问题我们称为黑盒问题，这类问题其表达式是未知的或者不可用的（比如因为保密性的要求，或者因问题本身极其复杂，设计优化算法的人无法在短时间内弄明白该问题等情况），但是对于给定的输入，可以得到函数的结果。这种情况下，无法计算问题的梯度等信息，只能通过比较解的函数值的方式来进行优化，所以很多传统的基于梯度的高效算法（比如牛顿法，拟牛顿法等）无法应用到这类问题上。对于这类问题，目前进化算法是一种常用的解决方案，但是进化算法存在收敛速度较慢，容易早熟收敛等一些缺点。因此对这类问题需要找到更好的优化方法加以解决。

除此之外，随着社会的发展和科学的进步，目前很多领域中的优化问题呈现出变量个数巨大（维度高）的特点，随着问题规模的扩大，问题的解决变得更加困难，现有的算法难以有效的解决这类问题。我们称这类变量个数多，维度高，问题规模大的优化问题为大规模全局优化问题（LSGO：Large Scale Global Optimization）。科学和工程中的很多问题诸如复杂的天线设计问题，航空航天领域问题等都可以建模为大规模全局优化问题来解决。大规模指的是问题的维数非常高，目前一般指的是不低于1000维。这类问题一般较为复杂，难以解决。而且目前很多算法仅对于中小规模的问题有效，对于大规模优化问题，如果直接应用这些算法，结果非常差。因此大规模全局优化问题是目前一类亟待解决的问题。由此可见，研究大规模全局优化问题不仅有理论意义，也有重要的实际应用价值。所以研究大规模全局优化算法是有意义的，也是十分必要的。

二、自适应梯度下降法求解大规模全局优化问题

考虑求解如下2000维大规模函数最值问题，设置最大迭代次数3000次

每次迭代中使用0.618法求解共轭梯度法中的最优步长

可以根据自己情况更改目标函数和迭代次数

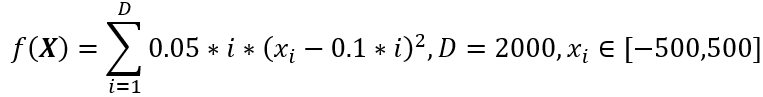
求解结果部分截图：

收敛曲线

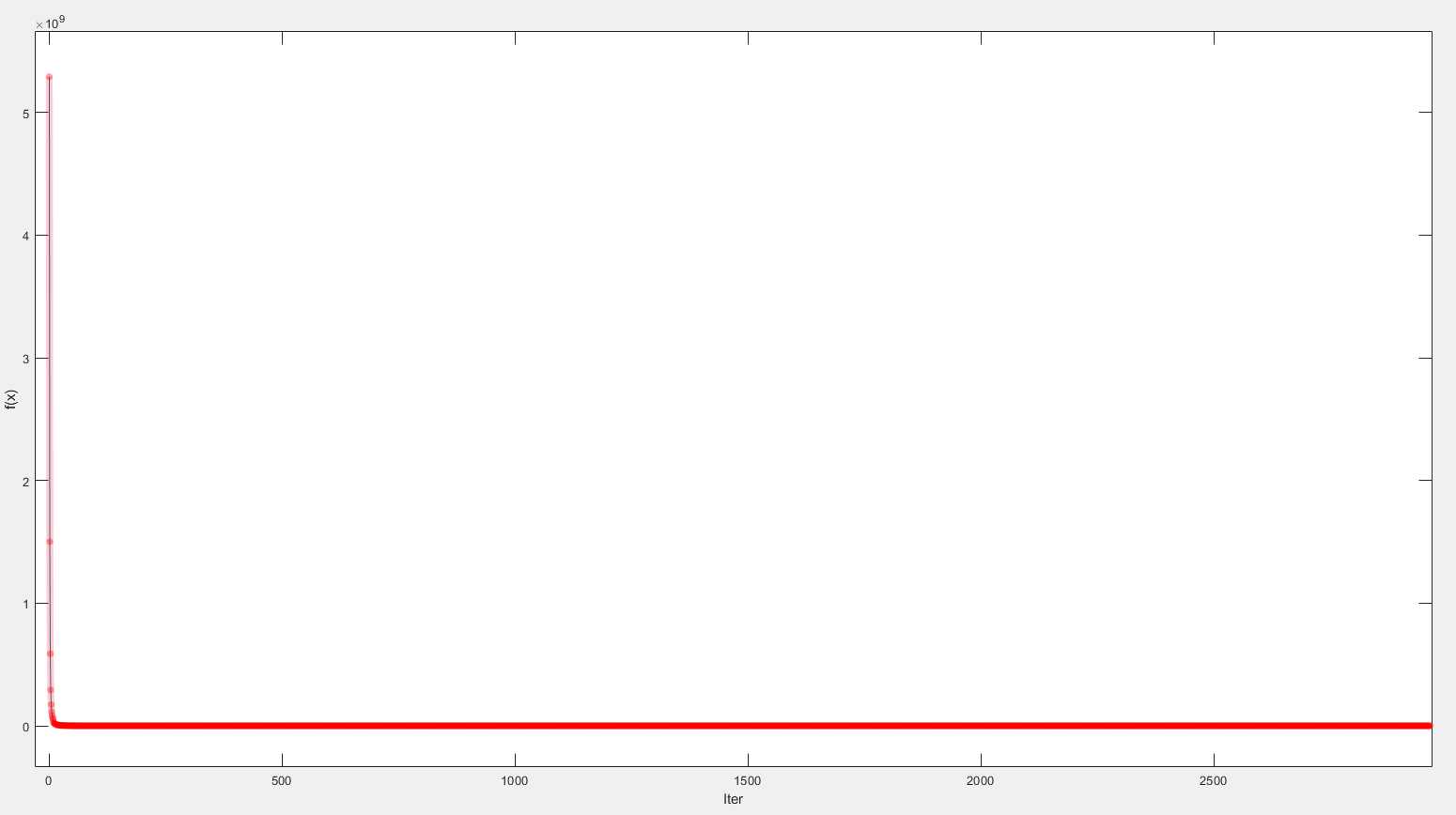
效果显著，自适应梯度下降方法求解该函数切实可行，可更换函数测试。