一、求解大规模全局优化问题存在困难

大规模全局优化问题是一类非常难解的问题，目前仍缺少有效的算法来高效的解决这类问题。大规模全局优化问题的困难之处主要表现在以下几个方面：

（1）    大规模问题涉及到的变量非常多，搜索空间巨大。问题的搜索空间随着问题的规模（维度）呈指数级增长。在有限的函数评估次数之内（可接受的时间范围内），算法难以有效的探寻如此巨大的搜索空间。而且问题的复杂程度随着维度的增加也随之增长，有些函数的性质随着维度的增加也有可能发生很大改变。很多对于低维非常有效的算法直接应用到大规模问题上效果变得非常差。

（2）    较为复杂的大规模问题存在数目巨大的局部最优解，因此算法容易陷入到某些局部最优值点。随着维度的增加，局部最优解的个数也急剧增多，甚至有些问题的局部最优解的个数是无限的，算法难以跳出所有的局部最优值到达全局最优解。

（3）    有些大规模问题是非凸，不可微的。大规模全局优化问题因其这些特性，使得传统的优化方法如最速下降法，牛顿法，拟牛顿法，共轭梯度法等无法有效的直接应用到大规模全局优化问题上，但目前各类自然启发算法仍然存在收敛速度慢等缺点

二、求解大规模全局优化问题的算法分类

求解大规模优化算法中，可以分为两大类：

1.    基于分解的算法：采用分组的方式，对大规模问题进行降维（分解），从而将大规模问题分解为多个子问题加以解决。多个子问题在协同进化框架下，分别使用进化算法进行优化；

2.    不直接分解大规模问题，而是通过结合多种局部搜索算法来进行优化。

三、共轭梯度法求解大规模全局优化问题

考虑求解如下3000维大规模函数最值问题，设置最大迭代次数800次

可以根据自己情况更改目标函数和迭代次数

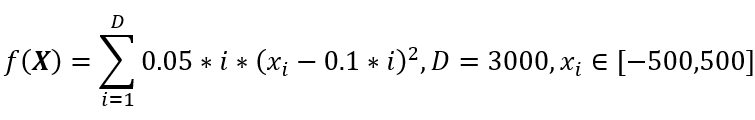
求解结果部分图：

收敛图：

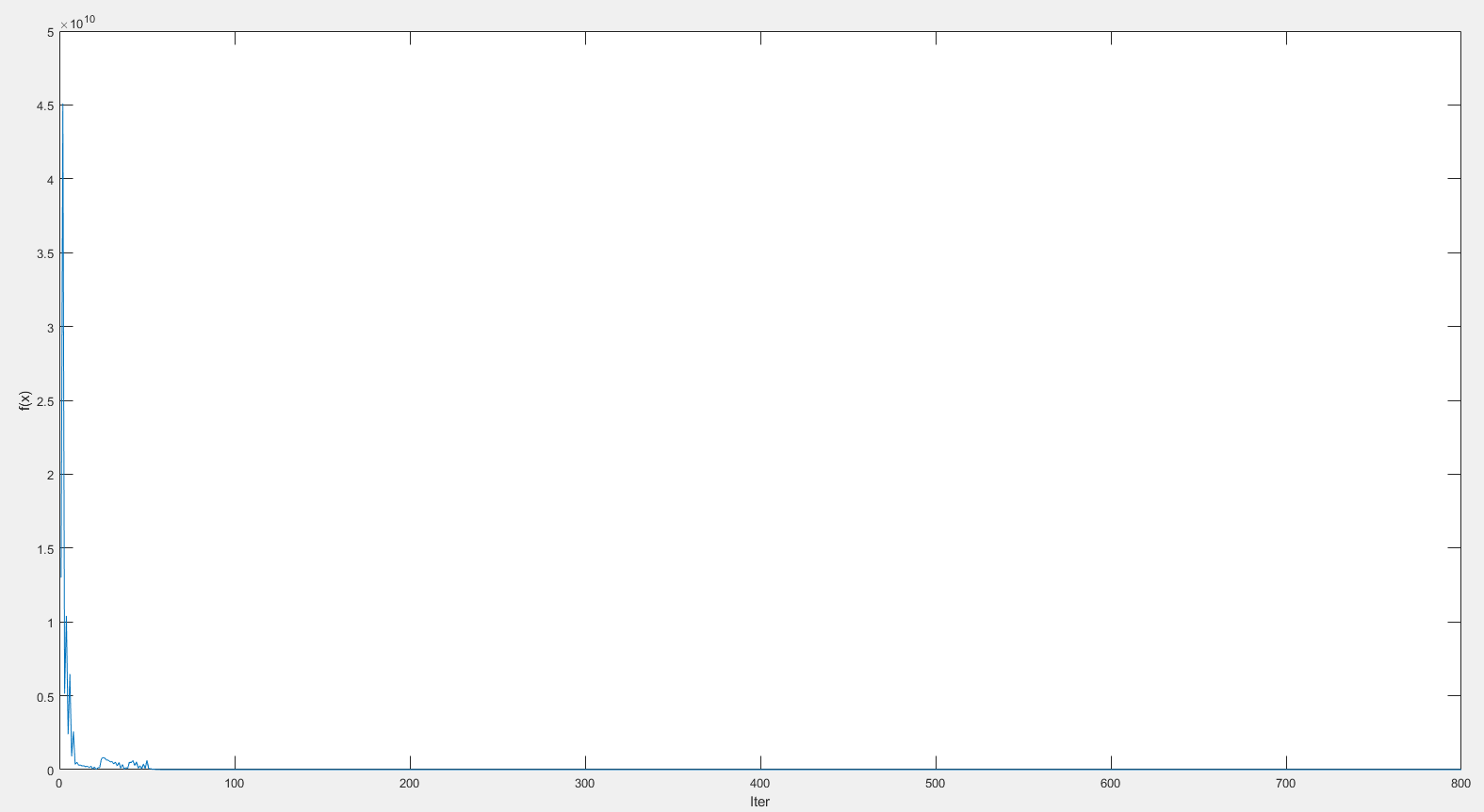
可以看出使用共轭梯度法求解该函数收敛速度快，效果显著。