一、最有价值球员算法

最有价值球员算法（Most Valuable Player Algorithm，MVPA）由Bouchekara 等人于2017年提出，该算法受到体育比赛的启发，球员们为了赢得冠军而组成队伍进行队伍竞争，他们也为了赢得最有价值球员( most valuable player，MVP) 奖杯进行独立竞争。在最有价值球员算法中，每个球员代表一个潜在的解，通过球员竞争和队伍竞争来不断提高球员的能力，最终产生一个 MVP，而 MVP 对应问题的最优解。

伪代码如下：

参考文献：

[1]王宁,刘勇.求解最优化问题的新型最有价值球员算法[J].计算机仿真,2020,37(06):273-282+327.

[2]缪炳荣,彭齐明,杨树旺,雒耀祥,裘杨喆.基于最有价值球员算法的结构损伤识别方法[J].重庆交通大学学报(自然科学版),2022,41(01):67-75.

[3]王宁,刘勇.考虑多种训练方式的自适应最有价值球员算法[J].计算机应用,2020,40(06):1722-1730.

[4]刘鑫. 最有价值球员算法及应用研究[D].广西民族大学,2019.DOI:10.27035/d.cnki.ggxmc.2019.000513.

[5]Bouchekara, Reh H . Most Valuable Player Algorithm: a novel optimization algorithm inspired from sport[J]. Operational Research, 2017.

二、旅行商问题（Traveling salesman problem, TSP）

旅行商问题（Traveling salesman problem, TSP）是一个经典的组合优化问题，它可以描述为一个商品推销员去若干城市推销商品，要求遍历所有城市后回到出发地，目的是选择一个最短的路线。当城市数目较少时，可以使用穷举法求解。而随着城市数增多，求解空间比较复杂，无法使用穷举法求解，因此需要使用优化算法来解决TSP问题。一般地，TSP问题可描述为：一个旅行商需要拜访n个城市，城市之间的距离是已知的，若旅行商对每个城市必须拜访且只拜访一次，求旅行商从某个城市出发并最终回到起点的一条最短路径。

三、求解结果

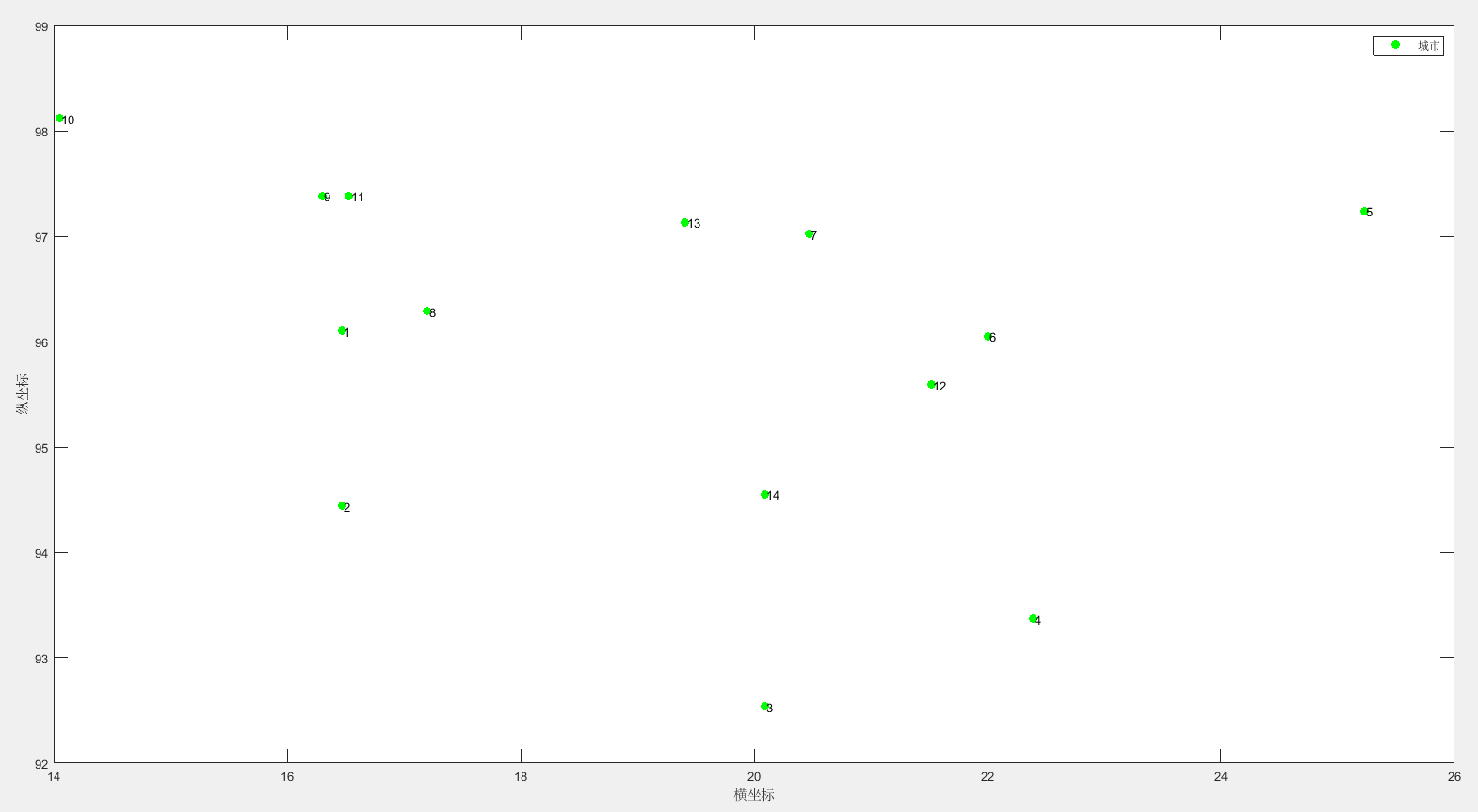
本文选取国际通用的TSP实例库TSPLIB中的测试集burma14，burma14中城市分布如下图所示：

本文采用最有价值球员算法求解burma14：

close all
clear
clc
%数据集参考文献  REINELT G.TSPLIB-a traveling salesman problem[J].ORSA Journal on Computing,1991,3(4):267-384.
%最有价值球员算法(Most Valuable Player Algorithm, MVPA)
global data
%burma14
Dim=size(data,1)-1;%维度
lb=-10;%下界
ub=10;%上界
fobj=@Fun;%计算总距离
SearchAgents_no=120; % 种群大小（可以修改）
Max_iteration=30; % 最大迭代次数（可以修改）
[bestX,fMin,curve]=MVPA(SearchAgents_no,Max_iteration,lb,ub,Dim,fobj);  %最有价值球员算法(Most Valuable Player Algorithm, MVPA)

其中一次结果：

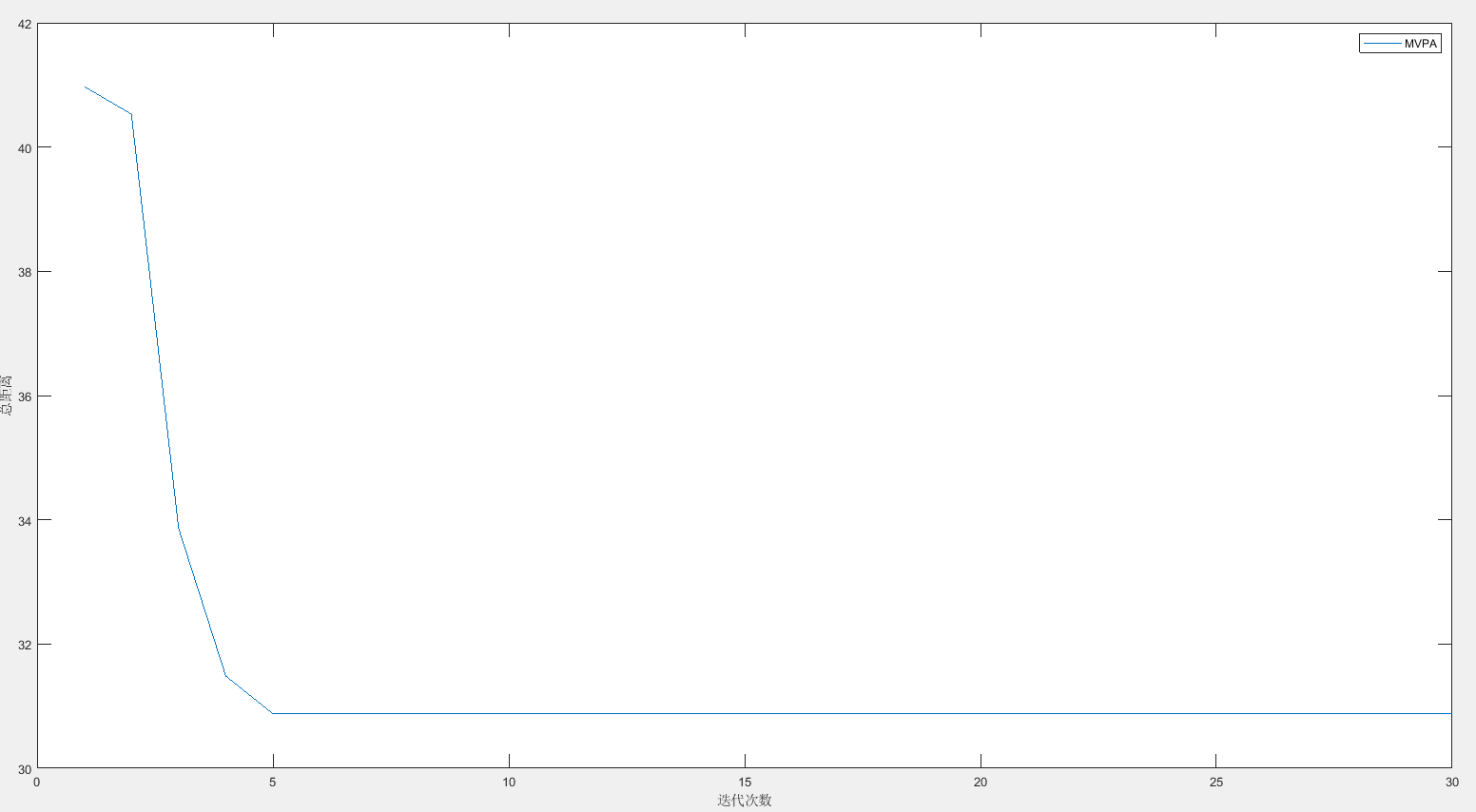
最有价值球员算法的收敛曲线：

最有价值球员算法求得的路径：

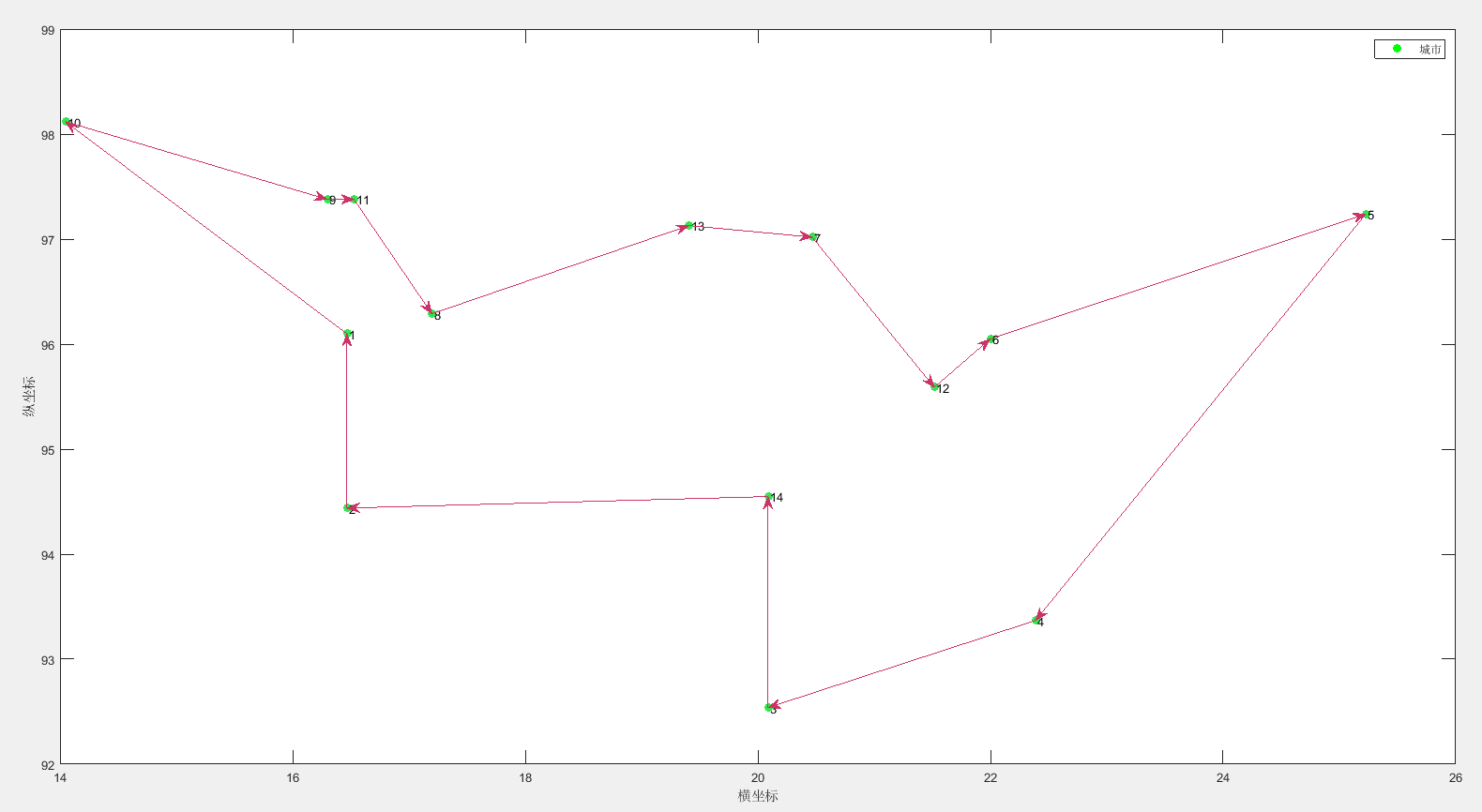
最有价值球员算法求解的最短总路径:30.8785

四、参考代码

文件夹内包含所有代码及使用说明，点击main.m即可运行。