1.软件版本

matlab2022a

2.运行方法

     使用matlab2022a或者高版本仿真，运行文件夹中的tops.m或者main.m。运行时注意matlab左侧的当前文件夹窗口必须是当前工程所在路径。具体操作观看提供的程序操作视频跟着操作。

3.部分仿真截图

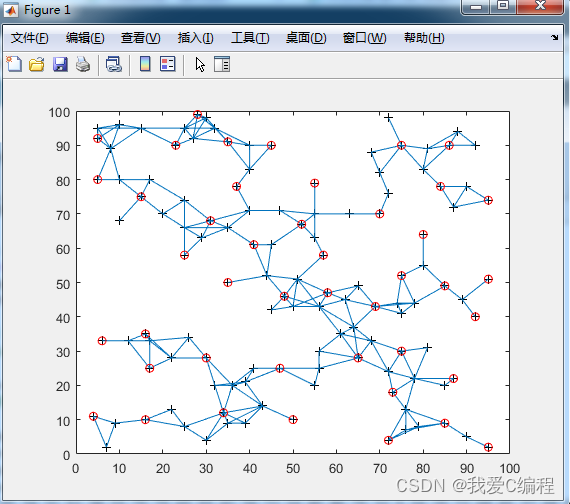
4.内容简介

  支配集的定义如下：给定无向图G =（V , E）,其中V是点集， E是边集， 称V的一个子集S称为支配集当且仅当对于V-S中任何一个点v, 都有S中的某个点u, 使得(u, v) ∈E。对于图G = (V, E) 来说,最小支配集指的是从 V 中取尽量少的点组成一个集合, 使得 V 中剩余的点都与取出来的点有边相连.也就是说,设 V' 是图的一个支配集,则对于图中的任意一个顶点 u ,要么属于集合 V', 要么与 V' 中的顶点相邻. 在 V' 中除去任何元素后 V' 不再是支配集, 则支配集 V' 是极小支配集.称G 的所有支配集中顶点个数最少的支配集为最小支配集,最小支配集中的顶点个数称为支配数.

     最小支配集(minimal dominating set)：对于图G=(V,E)来说，设V'是图G的一个支配集，则对于图中的任意一个顶点u，要么属于集合V'，要么与V'中的顶点相连。在V'中除去任何元素后V'不再是支配集，则支配集V'是极小支配集。称G中所有支配集中顶点个数最少的支配集为最小支配集，最小支配集中的顶点个数称为支配数。

最小支配集的性质：

1）求最小支配集问题被证明属于NP完全问题,即对于给定问题域的输入规模,目前尚无足够的手段证明该问题能够被判定在多项式时间内求解。

2）在含n个点的任意图中，若任意点的度大于等于3，则该图的最小支配集小于等于3n/8。

3）对于特殊图，如树，可使用贪心或dp的方法解决问题。

贪心策略

     首先选择一点为树根,再按照深度优先遍历得到遍历序列,按照所得序列的反向序列的顺序进行贪心,对于一个即不属于支配集也不与支配集中的点相连的点来说,如果他的父节点不属于支配集,将其父节点加入到支配集

具体实现

1.设整型数组dfn,fa,布尔数组vis,st。dfn[i]表示dfs中出现的第i个节点，fa[i]表示dfs中节点i的父节点，vis[i]-false表示节点i不属于支配集也不与支配集中的点相连，st[i]-true表示节点i在MDS中。

2.建图（邻接表）。

3.dfs一遍树，确定dfn,fa。

4.dfn逆序查找，确定vis,st,同时得出MDS。