基于概率论的MATLAB仿真,内容包括非共轭条件下的后验概率的推导,共轭条件下的非完备集的后验概率的推导,共轭条件下的完备集的后验概率的推导.
(包括程序操作录像+详细word设计文档+参考文献)
1.软件版本
matlab2022a
2.运行方法
使用matlab2022a或者高版本仿真,运行文件夹中的tops.m或者main.m。运行时注意matlab左侧的当前文件夹窗口必须是当前工程所在路径。具体操作观看提供的程序操作视频跟着操作。
3.部分仿真截图
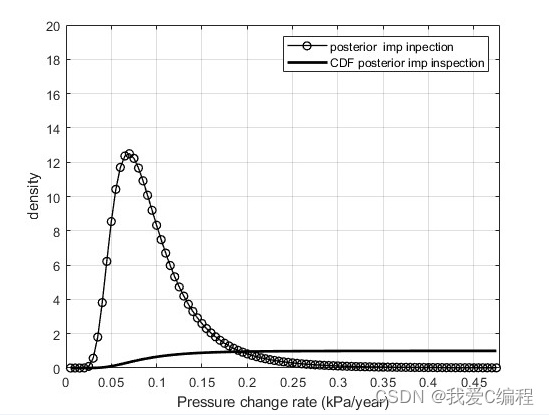
编辑
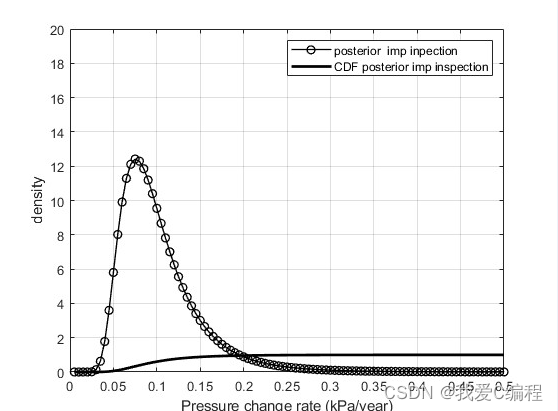
编辑
4.内容简介
根据贝叶斯概率论可知,某一事件的后验概率可以根据先验概率来获得,因此,这里首先对事件的先验概率分布进行理论的推导。假设测量的腐蚀数据服从gamma分布,其概率密度函数可以通过如下表达式表示:

编辑
根据参考文献1和参考文献2的理论推导可知,采用反gamma分布,可以作为腐蚀数据的先验分布,即:
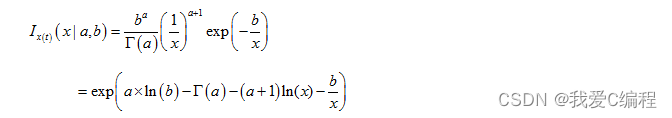
编辑
公式3为公式2的自然指数形式,公式3中,x表示腐蚀数据,参数a和b分别表示反gamma分布的参数估计值。

编辑

编辑
从公式7可知,此时后验概率值则取决于最后一次测量结果.根据上述推导过程,完备集的后验概率可以通过如下公式计算得到:
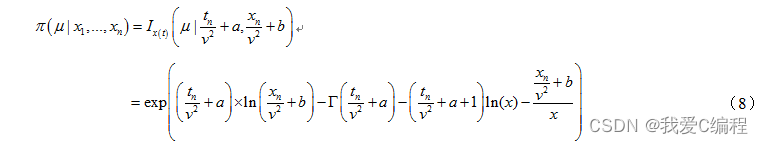
编辑
但是完备集下的后验概率所满足的公式3条件和公式4条件,在实际中往往不太可能发生,因此需要考虑非完备集下的后验概率计算方法。
1.2.共轭条件下的非完备集的后验概率的推导
完备集下的后验概率不太适用于实际情况,因此,对于实际情况,需要考虑非完备集下的后验概率的计算。非完备集下的后验概率是关于随机事件的条件概率,是在相关证据给定并纳入考虑之后的条件概率。后验概率和先验概率满足如下关系式:
![]()
编辑
从公式可知,后验概率等同于先验函数和似然函数的乘积,这里先验函数根据本文公式2获得,下面主要对似然函数进行公式推导,根据参考文献5的相关推导过程可知,后验概率的基本计算公式如下:

编辑
根据本文上述章节的介绍,参数A和B满足如下关系式:

编辑
因此,似然函数可以通过如下表达式表示:

编辑

编辑