1.软件版本
matlab2022a
2.运行方法
使用matlab2022a或者高版本仿真,运行文件夹中的tops.m或者main.m。运行时注意matlab左侧的当前文件夹窗口必须是当前工程所在路径。具体操作观看提供的程序操作视频跟着操作。
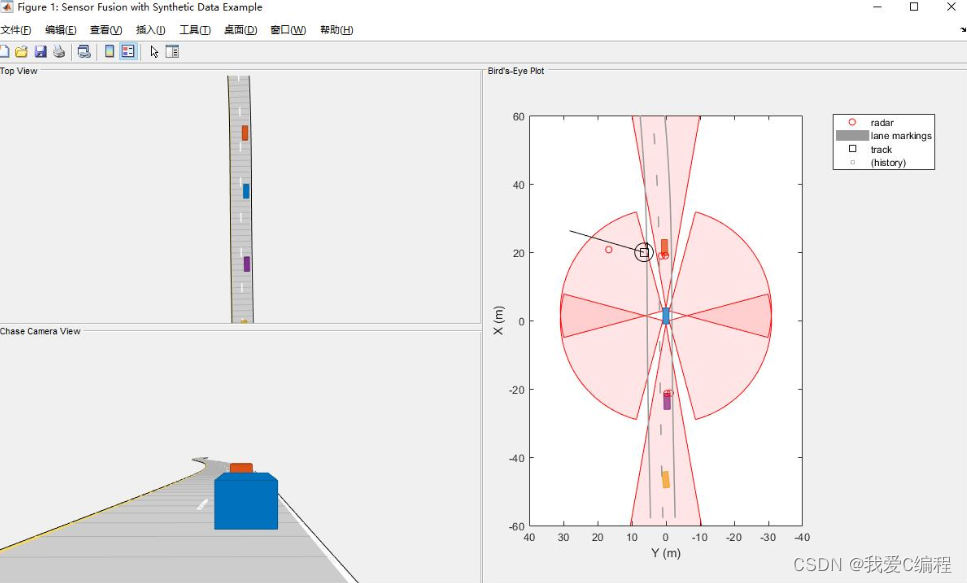
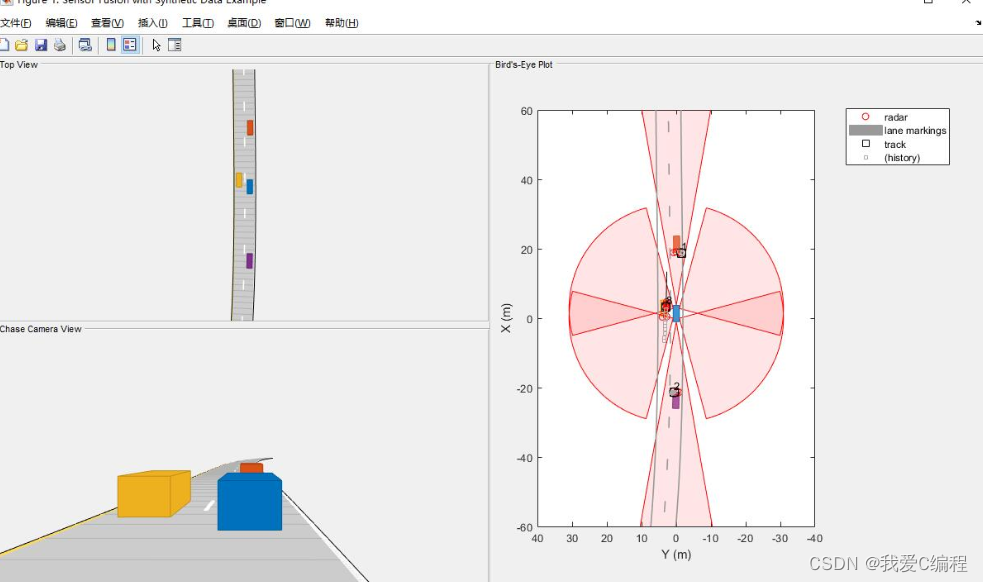
3.部分仿真截图
编辑
编辑
编辑
编辑
编辑
编辑
4.内容简介
EKF扩展卡尔曼滤波要解决的是卡尔曼滤波不适用于非线性模型的问题。其和卡尔曼滤波算法结构相同,只是将非线性模型线性化,然后再应用卡尔曼滤波完成状态估计。

编辑
扩展卡尔曼滤波的初始化,需要将各个变量进行设置,对于不同的运动模型,状态向量是不一样的。为了保证代码对不同状态向量的兼容性,我们使用Eigen库中非定长的数据结构。初始化扩展卡尔曼滤波器时需要输入一个初始的状态量x_in,用以表示障碍物最初的位置和速度信息,一般直接使用第一次的测量结果。这两个公式求的是卡尔曼滤波器中一个很重要的量——卡尔曼增益K(Kalman Gain),用人话讲就是求差值y的权值。第一个公式中的R是测量噪声矩阵(measurement covariance matrix),这个表示的是测量值与真值之间的差值。一般情况下,传感器的厂家会提供。
扩展卡尔曼(EKF)与经典卡尔曼(KF)的区别在于测量矩阵H的计算。EKF对非线性函数进行泰勒展开后,进行一阶线性化的截断,忽略了其余高阶项,进而完成非线性函数的近似线性化。正是由于忽略了部分高阶项,使得EKF的状态估计会损失一些精度。
卡尔曼滤波作为连续状态空间问题的一种解决方案,已经成功运用在火星登陆和自动导弹制导等领域。本质上卡尔曼滤波(Kalman Filter)是一置信度为正态分布的贝叶斯(Bayes Filter)滤波器,它的置信度可以表示为一个均值向量和协方差矩阵的形式,均值向量表示可能的状态,协方差矩阵表示该状态的不确定度。
前提假设
卡尔曼滤波需要满足以下三个前提假设,才能保证在任意一个时刻t的置信度bel(x(t))都是正态分布:
1) 运动模型必须是一个线性高斯模型。也就是说t+1时刻的状态必须是t时刻的状态的线性函数,附加一个高斯随机噪声。
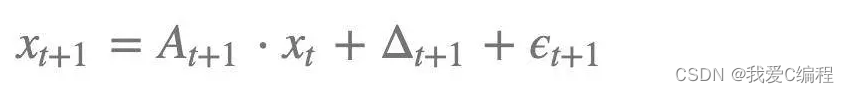
编辑
其中A是一个矩阵,Δ是运动向量,ξ是高斯随机噪声
2) 传感器模型也是一个线性高斯模型。
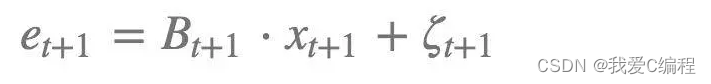
编辑
其中是一个矩阵,ζ表示传感器测量的高斯噪声。
3) 初始置信度bel(x0)是一个正态分布。
一维状态空间卡尔曼滤波
先从最简单的一维卡尔曼滤波说起,假设一辆小车以δ的速度和一定的随机噪声沿着一条直线前进,则它的运动方程:
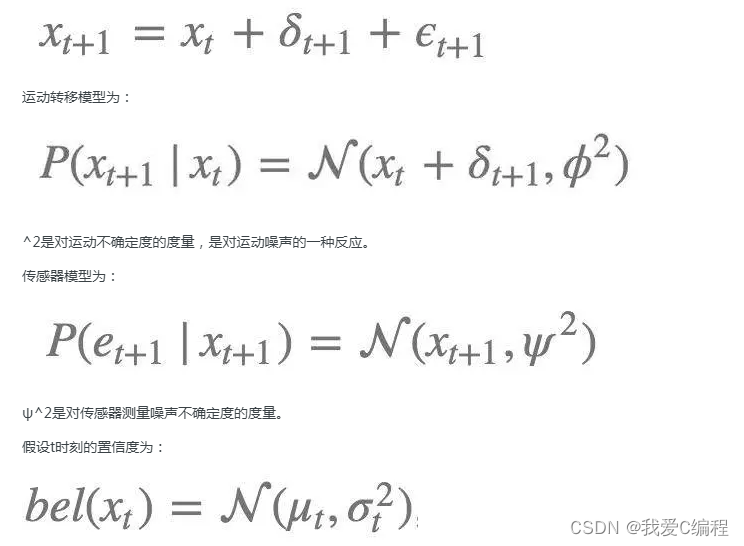
编辑
针对于线性高斯系统,卡尔曼滤波高效、简单、易行,然而遗憾的是在实际问题中,这样的理想的场景非常少。于是又有了扩展卡尔曼滤波,扩展卡尔曼滤波的思想是非线性系统在均值的一个小的邻域内可以近似认为是线性的,从而可以得到一个近似的高斯置信度。