1.软件版本

matlab2022a

2.运行方法

使用matlab2022a或者高版本仿真，运行文件夹中的tops.m或者main.m。运行时注意matlab左侧的当前文件夹窗口必须是当前工程所在路径。具体操作观看提供的程序操作视频跟着操作。

3.内容简介

    近年来，小波理论得到了非常迅速的发展，而且由于其具备良好的时频特性，因而实际应用也非常广泛。在去噪领域中，小波理论也同样受到了许多学者的重视，他们应用小波进行去噪并获得了非常好的效果。

具体来说小波去噪方法的成功主要得益于小波变换具有如下特点:

（1）低熵性，小波系数的稀疏分布，使得图象变换后的熵降低；

（2）多分辨率，由于采用了多分辨率的方法，所以可以非常好地刻画信号的非平稳特征，如边缘、尖峰、断点等；

（3）去相关性，因为小波变换可以对信号进行去相关，且噪声在变换后有白化趋势，所以小波域比时域更利于去噪；

（4）选基灵活性，由于小波变换可以灵活选择变换基，从而对不同应用场合，对不同的研究对象，可以选用不同的小波母函数，以获得最佳的效果。

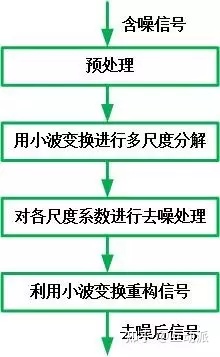
    小波去噪方法包括三个基本的步骤：对含噪声信号进行小波变换；对变换得到的小波系数进行某种处理，以去除其中包含的噪声；对处理后的小波系数进行小波逆变换，得到去噪后的信号。小波去噪方法的不同之处集中在第一步。

    相比以往的其他去噪方法，小波变换在低信噪比情况下的去噪效果较好，去噪后的信号识别率较高，同时小波去噪方法对时变信号和突变信号的去噪效果尤其明显。

​

编辑

利用小波分析对监测采集的信号进行去噪处理，可以恢复原始信号。利用小波分析进行去噪，包括以下3种方法：

• 默认阈值去噪处理：该方法利用函数ddencmp() 生成信号的默认阈值，然后利用函数wdencmp() 进行去噪处理；
• 给定阈值去噪处理：在实际的去噪处理过程中，阈值往往可通过经验公式获得，且这种阈值比默认阈值的可信度高。在进行阈值量化处理时可利用函数wthresh()；
• 强制去噪处理：该方法是将小波分解结构中的高频系数全部置0，即滤掉所有高频部分，然后对信号进行小波重构。这种方法比较简单，且去噪后的信号比较平滑，但是容易丢失信号中的有用成分。

​

4.部分仿真截图

​

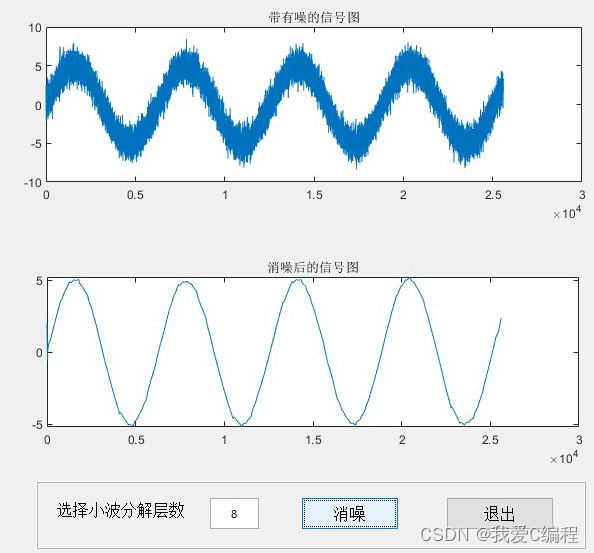
 ​编辑

​